Length Scales in Superfluid ³He

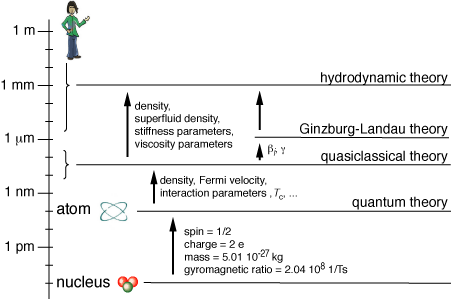
The figure presents some length scales that are important in theoretical studies of superfluid ³He. The shortest scale shown here is the nuclear scale, 0.01 pm. The nucleus consists of two protons and one neutron. One ³He atom consists of a nucleus and two circulating electrons. The size of the atom is approximately 0.1 nm, four orders of magnitude larger than the nuclear size. On the atomic scale and on larger scales the nucleus shows up only through the four parameters listed, the spin, the charge, the mass, and the gyromagnetic ratio.

The atoms in liquid ³He form a strongly interacting quantum system. Presently the theory of this liquid on the atomic scale is not very accurate. Fortunately, the behavior on longer length scales can well be understood with the quasiclassical theory [1]. This theory needs as input some parameters from the atomic level, in particular the density of the liquid, the Fermi velocity, the Landau interaction parameters, and the superfluid transition temperature T_c. At present these cannot be calculated at the atomic scale, but the most important ones can be extracted from experiments.

The quasiclassical theory represents a solution to the many-body problem of interacting ³He atoms. It becomes exact in the limit that the superfluid coherence length would be much larger than the atomic size. Since the coherence length is 15 nm ... 77 nm (depending on pressure), the quasiclassical theory represents a fairly good approximation. Instead of bare ³He atoms, there appears quasiparticles in the quasiclassical theory. The quasiparticles move like classical particles along (straight) trajectories, but along each trajectory there is quantum mechanical interference between particles flying in opposite directions. The quasiclassical theory contains as special cases the Bardeen-Cooper-Schrieffer theory of superconductivity and Landau's theory of Fermi liquids.

For macroscopic problems the quasiclassical theory is unnecessarily complicated. These problems can be more effectively studied with a hydrodynamic theory. The hydrodynamic theory for superfluid ³He is more complicated than for ordinary liquids because ³He can support frictionless flow of both mass and spin. In some problems the best approach is to use the Ginzburg-Landau theory of ³He. This theory works on a scale that is intermediate between the quasiclassical and hydrodynamic scales. Both the hydrodynamic and Ginzburg-Landau theory need some input parameters. It is important that these parameters can be calculated within the quasiclassical theory, since they are not easily accessible experimentally.

Examples of calculations at different scales:

• Hydrodynamic theory
  • Solitons in ³He-A
  • Vortex sheet in superfluid ³He-A and on the A-B interface
  • Phase diagram of vortices in superfluid ³He-A
  • Critical velocity of superfluid ³He-A
  • Hydrostatic theory of ³He-B
• Ginzburg-Landau theory
  • Vortex cores in superfluid ³He-B
  • π state in ³He Josephson junctions
  • Defect formation in inhomogeneous normal-superfluid transition
• Quasiclassical theory
  • Superfluid ³He in aerogel
  • π state in ³He Josephson junctions

[1] J.W. Serene and D. Rainer: The quasiclassical approach to superfluid ³He, Phys. Rep. 101, 221 (1983).

Back to helium theory page, to ³He page