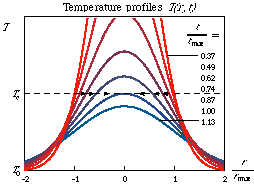

We are interested in experiments where superfluid 3He
is heated locally by a nuclear reaction.
Such experiments have been carried out by Osheroff et al at Stanford,
and more recently in
Helsinki and
Grenoble.
The energy released in the absorption of a neutron is sufficient
to heat the liquid
to a temperature far above the superfluid transition temperature Tc.
The figure illustrates how the temperature in the hot region relaxes back
towards its value T0 in the bulk.
We assume the simplest case where the cooling takes place by
heat conduction. The arrows denote how the normal-superfluid interface
propagates towards the center of the hot bubble.
It was argued that vortices and other defects are created in the
transition from the normal to the superfluid phase,
as predicted by Kibble and Zurek.
Our purpose is to study this taking into account the spatial
gradient of the temperature.
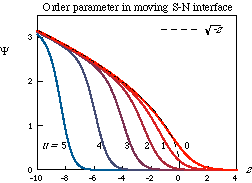 We study the propagation of the normal-superfluid front by time-dependent
Ginzburg-Landau (TDGL) theory. We find that the structure of the
interface depends only on one dimensionless parameter u.
It is proportional to the velocity of the temperature front
times the cube root of the length scale of the temperature gradient.
The figure shows the profile of the order parameter for different values of
u. The point z=0 corresponds to the point where T=Tc, and the
hot normal fluid is on the right hand side.
The superfluid interface lags behind this point by the distance
u2/4.
Fluctuations of the order parameter grow in this supercooled region.
For large u the supercooled region is so wide that fluctuations
strongly distort the
order parameter in the normal-superfluid front, and create vortices and other
defects within the bulk superfluid. Estimating the parameters we find that
vortices are formed by this mechanism in the neutron experiments. However,
also other processes may contribute to vortex creation in these experiments.
We study the propagation of the normal-superfluid front by time-dependent
Ginzburg-Landau (TDGL) theory. We find that the structure of the
interface depends only on one dimensionless parameter u.
It is proportional to the velocity of the temperature front
times the cube root of the length scale of the temperature gradient.
The figure shows the profile of the order parameter for different values of
u. The point z=0 corresponds to the point where T=Tc, and the
hot normal fluid is on the right hand side.
The superfluid interface lags behind this point by the distance
u2/4.
Fluctuations of the order parameter grow in this supercooled region.
For large u the supercooled region is so wide that fluctuations
strongly distort the
order parameter in the normal-superfluid front, and create vortices and other
defects within the bulk superfluid. Estimating the parameters we find that
vortices are formed by this mechanism in the neutron experiments. However,
also other processes may contribute to vortex creation in these experiments.
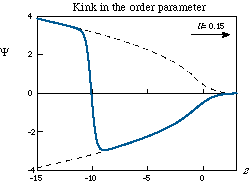 For slow transitions (u<1) the formation of defects depends on fluctuations
at a critical location of a defect. The figure shows a kink, which
can appear in a simple model where the order parameter is restricted to be
real valued. We find the critical location at z=-3/2u, where the kink
moves with the same velocity as the temperature front. If the kink is placed
nearer to the interface, it will move with a larger velocity and be
absorbed to the interface. If fluctuations are large enough to create the
kink at a larger distances from the interface, the kink will remain in the
superfluid because its velocity is smaller than that of the
normal-superfluid interface.
For slow transitions (u<1) the formation of defects depends on fluctuations
at a critical location of a defect. The figure shows a kink, which
can appear in a simple model where the order parameter is restricted to be
real valued. We find the critical location at z=-3/2u, where the kink
moves with the same velocity as the temperature front. If the kink is placed
nearer to the interface, it will move with a larger velocity and be
absorbed to the interface. If fluctuations are large enough to create the
kink at a larger distances from the interface, the kink will remain in the
superfluid because its velocity is smaller than that of the
normal-superfluid interface.
The theory described above has been continued by studying the instability of the normal-superfluid interface in the presence of externally applied superflow [1]. A review of the theories is given in Ref. [2].
Back to helium theory page
10.7.2000, Erkki Thuneberg, Email