Solitons in ³He-A

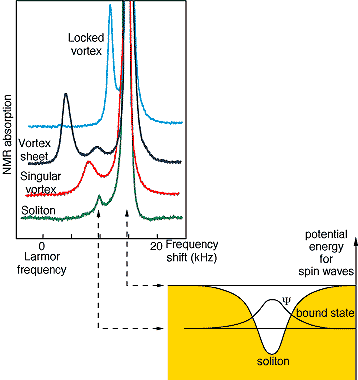Various topological objects and textures occur in superfluid ³He-A. The simplest of these are solitons. They are domain-wall like structures where a planar object separates two different but degenerate bulk states. Experimentally solitons are detected via satellite peaks that appear in the absorption spectrum of nuclear magnetic resonance (NMR). The frequencies of the peaks can be calculated by solving a Schrödinger-like equation for bound states in a potential caused by the soliton. We include dissipation by considering normal-superfluid conversion and spin diffusion. We compare the results with experiments and discuss their implications on the basic parameters of ³He. The agreement with experiments is good except a puzzling difference in the frequency of a splay soliton near the superfluid transition temperature.

A soliton forms the back-bone for a vortex sheet. Other topological objects in ³He-A are vortices and point defects.

Publications

• R. Hänninen and E.V. Thuneberg: Calculation of NMR properties of solitons in superfluid ³He-A, Phys. Rev. B 68, 094504 (2003), cond-mat 0103052.

Back to helium theory page