The latest planners based on SAT rival (and often exceed) the performance of planners based on other search paradigms. Additionally, this level of performance is obtained almost completely by general purpose SAT solving algorithms, without the need for the kind of specialized techniques used in connection with the recent state-space search planners. These developments to some extent explain the discrepancy between the algorithms of choice respectively in planning and in closely related forms of state-space search, e.g. model-checking in computer-aided verification (CAV): in CAV, explicit state-space search was dominant until early 1990s, and has since largely been supplanted by (symbolic) logic-based methods (first binary decision diagrams (BDD) and later SAT), whereas in AI planning, explicit state-space search was "discovered" only in late 1990s, and has sometimes been, for rather arbitrary reasons, considered the strongest search method by planning researchers.
Almost all of earlier research has used parallel plans based on the notion of interference: two actions are allowed to take place in parallel when they do not interfere. A sometimes dramatically more efficient planning is obtained with a more relaxed notion of plans, called ∃-step semantics, uses a more relaxed asymmetric notion of interference, which allows parallelization of actions in many cases where the no-interference condition is not satisfied. A further elaboration of the ∃-step semantics (for the more restricted class of STRIPS problems) is reported in a paper by Wehrle and Rintanen, Planning as satisfiability with relaxed ∃-step plans, where the conditions on parallel actions are further relaxed, in some cases leading to further performance improvements. These two ∃-step encodings are the fastest encodings in existence.
| plan type | description | references for encodings |
|---|---|---|
| sequential | exactly one (or at most one) action per time point | Kautz & Selman 1992; Kautz & Selman 1996 (factored encodings); Ernst et al. 1997 (factored encodings) |
| ∀-step plans ("GraphPlan parallelism") | A set of actions can be simultaneous if they are pairwise independent (more relaxed definition: can be executed in any order). | Kautz & Selman 1996 papers (original work); Rintanen et al. 2006 (compact and linear-size encodings); Robinson et al. 2009 (factored encodings) |
| ∃-step plans | A set of actions can be simultaneous if they can be totally ordered so that an earlier action does not disable a later action or change its (conditional) effects (more relaxed definition: can be executed in at least one order). | Dimopoulos et al. 1997 (original idea); Rintanen et al. 2004/2006 (analysis, encodings (linear-size)); Ogata et al. 2004 (more relaxed than the two above; also see Balyo 2013); Wehrle & Rintanen 2007 (less relaxed than Ogata) |
The smallest and generally most efficient encodings have an asymptotically optimal linear size, (which strongly contrasts with the quadratic size the encodings from the 1990s have). Further improvements, also for asymptotically optimal encodings, can be obtained by finding regularities which can be represented more compactly, most notably in the form of cliques and bicliques in constraint graphs formed by binary clauses (Rintanen 2006).
Some implementations, including BLACKBOX and its successors, use ∀-step plans, corresponding to GraphPlan's notion of parallel plans. These planners map (most of) the contents of the planning graphs to a SAT problem. The extremely large size of the planning graphs, and especially their high number of action mutexes, is the main reason for the extremely large size of the encodings these planners use (and the computation of the planning graphs takes excessively long in comparison to the time it takes to compute the invariants (Rintanen ECAI'08) which are the important subset of the fact mutexes in the graphs.) These encodings can be substantially improved by eliminating unnecessary action mutexes (Rintanen et al. 2006; Sideris & Dimopoulos, 2010).
It is sometimes believed that ∀-step plans represent "real" parallelism, and this is used as a justification when focusing on "optimal" (minimal horizon length) ∀-step plans. This idea, however, is wrong. Minimal horizon length ∀-step plans don't in general have anything to do with any practically interesting optimality criterion (e.g. minimum cost, minimum makespan). In particular, the definition of ∀-step plans does not guarantee that two actions that take place at the same step can actually be taken in parallel, or that two actions that interfere could not in reality be taken in parallel. Further, in those cases in which the problem modeling has guaranteed that the parallelism reflects reality (which could just as well be achieved with any other definition of parallel plans), usually the action durations vary so much that the minimal number of steps does not have much to do with minimal makespan: all the actions would have to have exactly the same duration for this to work (a condition rarely fulfilled.) For these reasons optimality interpreted as minimum horizon length is a rather uninteresting property of ∀-step plans, and similarly to other notions of parallel plans, the main purpose of the parallelism is as a method for reducing the size of the search space.
| algorithm | description | references |
|---|---|---|
| sequential | Solve SAT problems sequentially one at a time for horizon lengths 1, 2, 3, 4, ... until a plan is found. | Kautz & Selman 1992 |
| algorithm A | Start n SAT solvers simultaneously, solving the planning problem for horizon lengths 1,2,3,4,...,n. If a formula is found satisfiable, we have a plan, and terminate. If a formula is found unsatisfiable, start a solver for the shortest plan length not solved yet (first n+1, then n+2, n+3, and so on) so that there are always n SAT instances being solved. | Nabeshima et al. 2002; Rintanen 2004; Rintanen et al. 2006 |
| algorithm B | Solve horizon lengths 1,2,3,... in parallel, assigning to the SAT solver with horizon length t CPU time g times that of horizon length t-1, for some constant g<1. That is, the rate at which SAT problems are solved form a decreasing geometric sequence. Some finite bound is used for the number of SAT solvers run at any given moment (as determined by available memory.) | Rintanen 2004; Rintanen et al. 2006 |
| algorithm C | Solve horizon lengths 1,2,4,8,16,... in parallel, up to some finite length (some hundreds or thousands), with the same amount of CPU assigned to each horizon length. This strategy works surprisingly well, and does not rely on the implicit assumption that the horizon lengths are short. | Rintanen 2012 (unpublished) |
Other algorithms have been used, but they either don't lead to substantial runtime improvements (e.g. at most a small multiplicative factor like 2) and/or rely on the availability of plan length upper bounds which are not (efficiently) available. Algorithms A and B trade the possibility of a constant factor slow-down to a potentially arbitrarily high speed-up. Algorithm C does not have any practical performance guarantees w.r.t. A or B or the sequential strategy, but for problems with very long plans it is sometimes much better than A and B.
A prerequisite for the use of the efficient parallel search strategies is the compactness of the SAT encodings.
The first method that produced invariants for pruning the search space was the planning graph construction of GraphPlan (Blum and Furst, 1997). The invariants were a by-product of an approximate reachability computation, with invariants obtained as the fixpoint of the computation. Later algorithms have first made the computation more explicit (Rintanen KR'98), and later it has been substantially generalized (Rintanen, ECAI'08) to much more general forms of actions. The general fixpoint construction, though conceptually simple and natural, can be moderately expensive to implement, and some research has focused on simpler methods that find specific classes of invariants more efficiently.
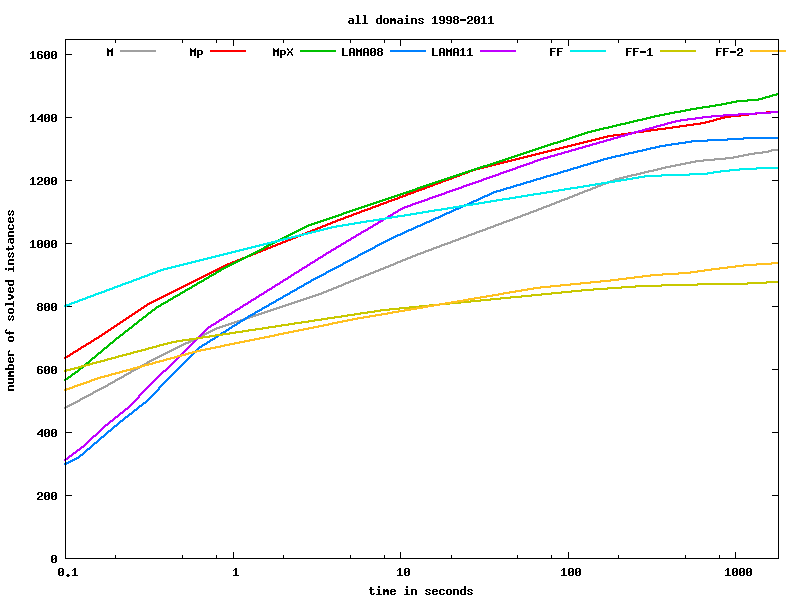
With the new heuristics, plans for many instances of standard benchmarks are found without backtracking (Airport, DriverLog, Gripper (all), Logistics (almost all), MPrime, Mystery, ParcPrinter, PSR, Rover, Satellite, Scanalyzer, Storage, Woodworking, ZenoTravel). Some of the instances with no or little backtracking (< 10 leaf nodes in the search tree) are not solved by the competition (= heuristic state-space search planners) in a reasonable amount of time (they cannot find plans in 5 minutes, and in some cases we have verified that no plans are found in 8 hours.)
Combinatorially harder problems, however, are still best solved with standard (generic) SAT heuristics, for example ones representing NP-complete graph problems.
(See also more diagrams, and data for each IPC domain, and the Planning as satisfiability: heuristics article for a wider set of problems, including ones for which most planners have not been tuned to.) The curve for FF's 2nd phase (FF-2) is a good approximation for Bonet & Geffner's original HSP planner's hypothetical extension to handle non-STRIPS problems with conditional effects.

The planning competition benchmarks are in general quite favorable to planners that use explicit state space search (which were developed by the planning competition community in tandem with the benchmark set), in comparison to other types of planning problems. Porco et al. (ICAPS'11) have translated graph problems into planning, and the picture from those results is quite a bit different. Here, general-purpose SAT solvers fare best by far (see more detailed discussion in the Porco et al. ICAPS'11 paper), followed by SAT with planning-specific heuristics as implemented in Mp.
| domain | instances | Mp | M | LAMA | FF | HSP | YAHSP |
|---|---|---|---|---|---|---|---|
| clique | 600 | 61 | 193 | 37 | 42 | 23 | 61 |
| coloring | 280 | 64 | 66 | 1 | 4 | 5 | 18 |
| Hamiltonian | 200 | 82 | 71 | 65 | 52 | 38 | 54 |
| k-colorability | 480 | 122 | 111 | 114 | 54 | 54 | 113 |
| matching | 160 | 69 | 80 | 35 | 0 | 0 | 33 |
| SAT | 200 | 41 | 78 | 39 | 1 | 20 | 0 |
| total | 1920 | 439 | 599 | 291 | 153 | 140 | 279 |
J. Rintanen. Planning as satisfiability: heuristics, Artificial Intelligence Journal, 2012.
J. Rintanen. Engineering efficient planners with SAT, In ECAI 2012. Proceedings of the 20th European Conference on Artificial Intelligence, IOS Press, 2012.
J. Rintanen. Planning with specialized SAT solvers. In Proceedings of the AAAI Conference on Artificial Intelligence, AAAI Press, pages 1563-1566, 2011. (© 2011 American Association for Artificial Intelligence. AAAI) (slides)
J. Rintanen. Planning with SAT, admissible heuristics and A*. In Proceedings of the International Joint Conference on Artificial Intelligence, AAAI Press, pages 2015-2020, 2011. (© 2011 American Association for Artificial Intelligence. AAAI)
J. Rintanen. Heuristics for planning with SAT and expressive action definitions. In Proceedings of the International Conference on Automated Planning and Scheduling, AAAI Press, pages 210-217, 2011. (© 2011 American Association for Artificial Intelligence. AAAI)
Jussi Rintanen. Heuristic planning with SAT: beyond strict depth-first search. Twenty-Third Australasian Joint Conference on Artificial Intelligence, Adelaide, December 7-10, 2010, Proceedings. Lecture Notes in Computer Science, Springer-Verlag, 2010.
Jussi Rintanen. Heuristics for planning with SAT. In David Cohen, ed., Principles and Practice of Constraint Programming - CP 2010, 16th International Conference, CP 2010, St. Andrews, Scotland, September 2010, Proceedings. Lecture Notes in Computer Science 6308, pages 414-428, Springer-Verlag, 2010.
J. Rintanen. Regression for classical and nondeterministic planning. In Malik Ghallab, Constantine D. Spyropoulos, and Nikos Fakotakis, editors, ECAI 2008. Proceedings of the 18th European Conference on Artificial Intelligence. pages 568-571, IOS Press, 2008.
Jussi Rintanen. Planning graphs and propositional clause-learning. In Gerhard Brewka and Patrick Doherty, editors, Principles of Knowledge Representation and Reasoning: Proceedings of the Eleventh International Conference (KR 2008), pages 535-543, AAAI Press, 2008.
M. Wehrle and J. Rintanen, Planning as satisfiability with relaxed ∃-step plans, In M. Orgun and J. Thornton, eds, AI 2007 : Advances in Artificial Intelligence: 20th Australian Joint Conference on Artificial Intelligence, Surfers Paradise, Gold Coast, Australia, December 2-6, 2007, Proceedings, Lecture Notes in Computer Science 4830, pages 244-253, Springer-Verlag, 2007. The winner of the AI 2007 Best Paper Award
J. Rintanen, K. Heljanko and I. Niemelä, Planning as satisfiability: parallel plans and algorithms for plan search, Artificial Intelligence, 170(12-13), pages 1031-1080, 2006.
J. Rintanen, Evaluation strategies for planning as satisfiability, in R. Lopez de Mantaras and Lorenza Saitta, eds., ECAI 2004. Proceedings of the 16th European Conference on Artificial Intelligence, pages 682-687, IOS Press, 2004. [additional material on slides of ECAI'04 talk, 4 on 1]
J. Rintanen, Phase transitions in classical planning: an experimental study, in Principles of Knowledge Representation and Reasoning: Proceedings of the Ninth International Conference (KR 2004), pages 710-719, AAAI Press, 2004. [additional material on slides of KR'04 talk, 8 on 1]
J. Rintanen, Compact representation of sets of binary constraints, ECAI 2006. Proceedings of the 17th European Conference on Artificial Intelligence, pages 143-147, IOS Press, 2006. [ECAI'06 talk] Biclique-based representations of binary constraints for improving the scalability of SAT representations for very large planning problems.
J. Rintanen, Symmetry reduction for SAT representations of transition systems, in Proceedings of the 13th International Conference on Automated Planning and Scheduling, pages 32-40, AAAI Press, 2003. (© 2003 American Association for Artificial Intelligence. All rights reserved. AAAI)
J. Rintanen and H. Jungholt. Numeric state variables in constraint-based planning, in Recent Advances in AI Planning: 5th European Conference on Planning, ECP'99, Durham, UK, September 8-10, 1999, S. Biundo and M. Fox, eds., Lecture Notes in Artificial Intelligence 1809, pages 109-121, 2000. Springer-Verlag, Berlin, Germany.
J. Rintanen. Constructing conditional plans by a theorem-prover, Journal of Artificial Intelligence Research, 10:323-352, 1999. (JAIR)
J. Rintanen. A planning algorithm not based on directional search. in Principles of Knowledge Representation and Reasoning: Proceedings of the Sixth International Conference (KR '98), A. G. Cohn, L. K. Schubert, and S. C. Shapiro, eds., pages 617-624, Trento, Italy, June 1998. Morgan Kaufmann Publishers, San Francisco, California.
M. Büttner and J. Rintanen, Satisfiability planning with constraints on the number of actions, in Proceedings of the 15th International Conference on Automated Planning and Scheduling, pages 292-299, AAAI Press, 2005.
Overviews:
J. Rintanen, Planning and SAT, in A. Biere, M. Heule, H. van Maaren and T. Walsh, Handbook of Satisfiability, IOS Press, 2009.
J. Rintanen. State-space traversal techniques for planning, Albert-Ludwigs-Universität-Freiburg, Institut für Informatik, Technical Report 220, 76 pages, 2005. (IJCAI-13 Tutorial)
J. Rintanen. Introduction to automated planning, course notes, Albert-Ludwigs-Universität Freiburg, 2003-2005.
Y. Dimopoulos, B. Nebel and J. Koehler, Encoding planning problems in nonmonotonic logic programs, European Conference on Planning, Springer-Verlag, 1997.
H. Kautz and B. Selman, Planning as satisfiability, Proceedings of the Tenth European Conference on Artificial Intelligence (ECAI'92), John Wiley, 1992.
H. Kautz and B. Selman, Pushing the envelope: planning, propositional logic, and stochastic search, Proceedings of the Thirteenth National Conference on Artificial Intelligence and the Eighth Innovative Applications of Artificial Intelligence Conference, AAAI Press, 1996.
N. Robinson, C. Gretton, D.-N. Pham and A. Sattar, SAT-based parallel planning using a split representation of actions, International Conference on Automated Planning and Scheduling, AAAI Press, 2009.