\(%\usepackage{color}\) \(%\usepackage{tcolorbox}\) \(%\tcbuselibrary{skins}\) \(\usepackage{pifont}\) \(\) \(%\definecolor{aaltoblue}{RGB}{00,101,189} % 0065BD\) \(%\definecolor{aaltored}{RGB}{237,41,57} % ED2939\) \(\) \(\definecolor{MyBoxBackground}{rgb}{0.98,0.98,1.0}\) \(\definecolor{MyBoxBorder}{rgb}{0.90,0.90,1.0}\) \(%\definecolor{backgroundred}{rgb}{1.0,0.98,0.98}\) \(%\definecolor{shadowred}{rgb}{1.0,0.90,0.90}\) \(\) \(%\newcommand{\subheading}[1]{\textbf{\large\color{fakeaaltobluel}#1}}\) \(\newcommand{\subheading}[1]{\large{\usebeamercolor[fg]{frametitle}\sc #1}}\) \(\) \(\newcommand{\AAccess}[1]{{\footnotesize[\href{https://libproxy.aalto.fi/login?url=#1}{Aalto lib access}]}}\) \(%\newtcbox{\mybox}[1][red]{on line,arc=0pt,outer arc=0pt,colback=#1!10!white,colframe=#1!50!black,boxsep=0pt,left=1pt,right=1pt,top=2pt,bottom=2pt,boxrule=0pt,bottomrule=1pt,toprule=1pt}\) \(%\newtcbox{\mybox}[1][MyBoxBackground]{on line,arc=0pt,outer arc=0pt,colback=#1!10!white,colframe=#1!50!black,boxsep=0pt,left=1pt,right=1pt,top=2pt,bottom=2pt,boxrule=0pt,bottomrule=1pt,toprule=1pt}\) \(\) \(\newtcolorbox{MyBoxTitled}[1]{colback=MyBoxBackground!100!black,colframe=MyBoxBorder!100!black,boxsep=2pt,left=0pt,right=0pt,top=2pt,bottom=0pt,%enhanced,%\) \( coltitle=red!25!black,title=#1,boxrule=1pt}\) \(\) \(\newtcolorbox{MyBox}[1][]{colback=MyBoxBackground!100!black,colframe=MyBoxBorder!100!black,boxsep=0pt,left=2pt,right=0pt,top=0pt,bottom=0pt,%enhanced,%\) \( coltitle=red!25!black,boxrule=1pt,#1}\) \(\) \(\newenvironment{EqnBox}[1]{\begin{adjustbox}{valign=t}\begin{minipage}{#1}\begin{MyBox}[colback=italyGreen!10!white,colframe=italyGreen!100!black]}{\end{MyBox}\end{minipage}\end{adjustbox}}\) \(\) \(\newenvironment{topbox}[1]{\begin{adjustbox}{valign=t}\begin{minipage}{#1}}{\end{minipage}\end{adjustbox}}\) \(\) \(\newcommand{\Blue}[1]{{\color{finnishBlue}#1}}\) \(\newcommand{\Red}[1]{{\color{italyRed}#1}}\) \(%\newcommand{\Emph}[1]{\emph{\color{aaltoblue}#1}}\) \(\newcommand{\Emph}[1]{\emph{\usebeamercolor[fg]{structure} #1}}\) \(%\newcommand{\Emp}{\usebeamercolor[fg]{structure}}\) \(\newcommand{\Emp}{\color{italyRed}}\) \(\newcommand{\TextDef}[1]{{\bf\usebeamercolor[fg]{structure} #1}}\) \(\) \(\newcommand{\todo}[1]{\textbf{\Red{\Pointer #1}}}\) \(\newcommand{\TODO}[1]{\todo{#1}}\) \(\) \(\newcommand{\Pointer}{\raisebox{-1ex}{\huge\ding{43}}\ }\) \(\) \(%\newcommand{\Follows}{\Pointer}\) \(\newcommand{\Follows}{\color{finnishBlue}\rightsquigarrow}\) \(\newcommand{\Property}{{\color{italyGreen}\bf Property}}\) \(\) \(\) \(%\) \(% Common math definitions\) \(%\) \(\newcommand{\Set}[1]{\{#1\}}\) \(\newcommand{\Setdef}[2]{\{{#1}\mid{#2}\}}\) \(\newcommand{\PSet}[1]{\mathcal{P}(#1)}\) \(\newcommand{\Pair}[2]{(#1,#2)}\) \(\newcommand{\Card}[1]{{\vert{#1}\vert}}\) \(\newcommand{\Tuple}[1]{(#1)}\) \(\newcommand{\Seq}[1]{[#1]}\) \(\newcommand{\bbZ}{\mathbb{Z}}\) \(\newcommand{\Ints}{\mathbb{Z}}\) \(\newcommand{\Reals}{\mathbb{R}}\) \(\newcommand{\bbQ}{\mathbb{Q}}\) \(\newcommand{\Rats}{\bbQ}\) \(\) \(\newcommand{\False}{\textsf{F}}\) \(\newcommand{\True}{\textsf{T}}\) \(\) \(\newcommand{\Implies}{\rightarrow}\) \(\newcommand{\Iff}{\leftrightarrow}\) \(%\newcommand{\Implies}{\Rightarrow}\) \(%\newcommand{\Iff}{\Leftrightarrow}\) \(\newcommand{\Xor}{\oplus}\) \(\) \(\newcommand{\Equiv}{\equiv}\) \(\) \(\newcommand{\Oh}[1]{O(#1)}\) \(%\newcommand{\Theta}[1]{\Theta(#1)}\) \(\) \(\newcommand{\PHP}[2]{\mathrm{php}_{#1,#2}}\) \(\newcommand{\PH}[2]{\mathit{x}_{#1,#2}}\) \(\) \(\newcommand{\NP}{\textbf{NP}}\) \(\newcommand{\coNP}{\textbf{co-NP}}\) \(\) \(\newcommand{\bnfdef}{\mathrel{\textup{::=}}}\) \(\newcommand{\bnfor}{\mathrel{\mid}}\) \(\)

\(\newcommand{\Asgn}{\leftarrow}\) \(\newcommand{\PseudoDPLL}{\mathop{\textrm{DPLL}}}\) \(\newcommand{\PseudoCDCL}{\mathop{\textrm{CDCL}}}\) \(\newcommand{\PseudoAsgn}{\mathrel{\leftarrow}}\) \(\newcommand{\PseudoUnsat}{\mathbf{unsat}}\) \(\newcommand{\PseudoSat}{\mathbf{sat}}\) \(\newcommand{\PseudoUP}{\mathop{\textit{unit-propagate}}}\) \(\newcommand{\PseudoAnalyze}{\mathop{\textit{analyze-conflict}}}\) \(\) \(%\newcommand{\Neg}[1]{\overline{#1}}\) \(\newcommand{\Neg}[1]{\neg #1}\) \(\newcommand{\Vars}{X}\) \(\newcommand{\VarsOf}[1]{\mathop{vars}(#1)}\) \(\) \(\newcommand{\TA}{\tau}\) \(\newcommand{\Undef}{\mathit{undef}}\) \(\) \(%\newcommand{\Form}{\phi}\) \(\newcommand{\Models}{\models}\) \(\) \(\newcommand{\Trail}{\pi}\) \(\newcommand{\Anno}[2]{#1^{#2}}\) \(\newcommand{\Lit}{l}\) \(\newcommand{\Reason}{r}\) \(\newcommand{\Dec}{\textsf{dec}}\) \(\) \(\newcommand{\IG}[1]{G_{#1}}\) \(\newcommand{\IGVerts}{V}\) \(\newcommand{\IGEdges}{E}\) \(\newcommand{\IGEdge}[2]{\Pair{#1}{#2}}\) \(\newcommand{\IGConflict}{\bot}\) \(\newcommand{\Cut}{W}\) \(\) \(\newcommand{\ResOp}[1]{\mathrel{\otimes_{#1}}}\) \(\newcommand{\Res}[3]{#1 \ResOp{#3} #2}\)

The resolution proof system

Suppose that you run a SAT solver on your problem instance and the solver answers “the formula is satisfiable” and provides you a satisfying truth assingment. It is now quite easy to check that the verdict is correct: just evaluate the formula under the assignment and check that all the clauses are satisfied.

However, if the solver simply returns “the formula is unsatisfiable”, can you trust the solver? Although the current SAT solvers are very robust, a bug in the complex implementation of a solver is still a possibility. In many applications this possibility can arguably be ignored but in some others, such as using SAT solvers to prove open mathematical problems, one really wants to verify that there are no solutions. Some solvers can in fact also produce proofs of unsatisfiability. Such proofs can be independently and automatically checked by some (relatively simple and possibly formally verified) proof checking tool. In the following, we introduce the classic proof system called resolution. The best tools at the moment use something more complicated but these are not covered in this course.

The resolution proof system is a proof system for CNF formulas that is based on taking “resolvents” of two clauses.

Definition: Resolvent of two clauses

Let \(C_1 = (x \lor l_1 \lor l_2 \lor ... \lor l_k)\) and \(C_2 = (\neg x \lor l'_1 \lor l'_2 \lor ... \lor l'_p)\) be two clauses and \(x\) any variable. The resolvent of \(C_1\) and \(C_2\) with respect to \(x\) is the clause \(\Res{C_1}{C_2}{x} = (l_1 \lor l_2 \lor ... \lor l_k \lor l'_1 \lor l'_2 \lor ... \lor l'_p)\).

Example

• ​ The resolvent of \((x \lor y \lor \neg z)\) and \((\neg y \lor \neg z \lor w)\) is with respect to \(y\) the clause \((x \lor \neg z \lor w)\).

• ​ The resolvent of \((x)\) and \((\neg x)\) is the empty clause \(()\).

• ​ The resolvent of \((x \lor y \lor z)\) and \((\neg y \lor \neg z \lor w)\) with recpect to \(y\) is \((x \lor z \lor \neg z \lor w)\), a tautology.

The key fact is that the resolvent \(\Res{C_1}{C_2}{x}\) is a logical consequence of \(C_1 \land C_2\), where \(C_1 = (x \lor l_1 \lor l_2 \lor ... \lor l_k)\) and \(C_2 = (\neg x \lor l'_1 \lor l'_2 \lor ... \lor l'_p)\). One can reason this as follows. First, \(x\) must be either false or true in any truth assignment that satisfies \(C_1 \land C_2\). If \(x\) is false, one of \(l_1,l_2,...,l_k\) must be true in a truth assignment satisfying \(C_1\). Similarly, if \(x\) is true, then one of \(l'_1,l'_2,...,l'_p\) must be true. Therefore, in any case one of \(l_1,l_2,...,l_k,l'_1,l'_2,...,l'_p\) must be true in a truth assignment satisfying \(C_1 \land C_2\) and thus \(\Res{C_1}{C_2}{x}\) is a logical consequence of \(C_1 \land C_2\).

Definition: Resolution proofs of unsatisfiability

A resolution proof of unsatisfiability of a CNF formula \(\phi\) is a finite sequence \(C_1,C_2,...,C_m\) of clauses such that each clause \(C_i\) in it is a non-tautology and either

1. a clause in the formula \(\phi\), or

2. the resolvent of two earlier clauses \(C_j\) and \(C_k\), \(j,k < i\), in the sequence.

Furthermore, the last clause \(C_m\) must be the empty clause \(()\) that is not satisfied in any truth assignment.

The resolution proof system is both (i) sound, meaning that if a formula has a resolution proof of unsatisfiability, then it actually is unsatisfiable, and (ii) complete, meaning that for each unsatisfiable CNF formula there is a resolution proof of unsatisfiability. Therefore, a formula \(\phi\) is unsatisfiable if and only if there is a resolution proof of unsatisfiability for it.

Example

Consider again the unsatisfiable CNF formula

\[\phi = (a \lor \neg b) \land (\neg a \lor c \lor \neg d) \land (a \lor c \lor \neg d) \land (\neg c \lor \neg e) \land (\neg c \lor e) \land (c \lor d).\]

A resolution proof of its unsatisfiability is the sequence \(C_1,...,C_9\) where

• ​ \(C_1 = (\neg c \lor e)\), a clause in the formula \(\phi\)

• ​ \(C_2 = (\neg c \lor \neg e)\), a clause in the formula \(\phi\)

• ​ \(C_3 = (\neg c)\), the resolvent \(\Res{C_1}{C_2}{e}\)

• ​ \(C_4 = (a \lor c \lor \neg d)\), a clause in the formula \(\phi\)

• ​ \(C_5 = (\neg a \lor c \lor \neg d)\), a clause in the formula \(\phi\)

• ​ \(C_6 = (c \lor \neg d)\), the resolvent \(\Res{C_4}{C_5}{c}\)

• ​ \(C_7 = (c \lor d)\), a clause in the formula \(\phi\)

• ​ \(C_8 = (c)\), the resolvent \(\Res{C_6}{C_7}{d}\)

• ​ \(C_9 =()\), the resolvent \(\Res{C_3}{C_8}{c}\)

Finding resolution proofs of unsatisfiability directly can be difficult for humans especially. However, the search tree of DPLL without unit propagation (recall the section The DPLL backtracking search procedure) can be converted to a resolution proof quite easily:

1. attach each dead-end node with one clause that is falsified in it

2. attach each other node with

   • ​ the clause of one of its children if that clause does not involve the branching variable of the node, or

   • ​ the resolvent of the clauses in its two children otherwise

3. the root will be attached with the empty clause

4. list the clauses attached in the tree in post-order

The correctness can be shown by structural induction on the tree, showing that the clause attached to each node contains only literals that are negations of the ones in its partial truth assignment. The proofs obtained in this way are actually tree-like resolution proofs, where a clause obtained by using the resolution proof is used only once. For some formula families, such proofs can be superpolynomially larger than the ones that can be obtained with unrestricted resolution.

Example

Consider again the CNF formula \((a \lor \neg b) \land (\neg a \lor c \lor \neg d) \land (a \lor c \lor \neg d) \land (\neg c \lor \neg e) \land (\neg c \lor e) \land (c \lor d)\). Annotating the search tree nodes with clauses as described above, we get

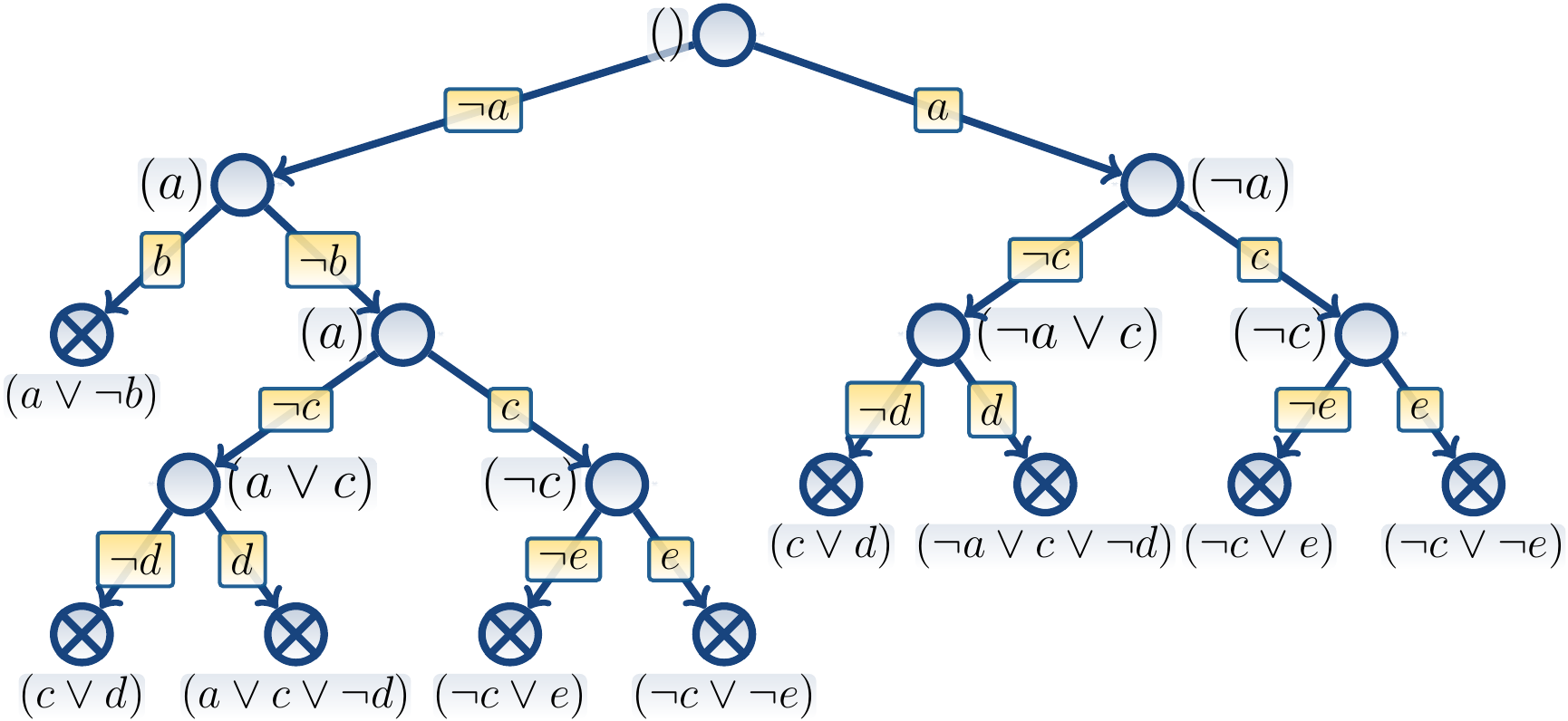
This corresponds to the resolution proof of unsatisfiability \((a \lor \neg b)\), \((c \lor d)\), \((a \lor c \lor \neg d)\), \((a \lor c)\), \((\neg c \lor e)\), \((\neg c \lor \neg e)\), \((\neg c)\), \((a)\), \((a)\), \((c \lor d)\), \((\neg a \lor c \lor \neg d)\), \((\neg a \lor c)\), \((\neg c \lor e)\), \((\neg c \lor \neg e)\), \((\neg c)\), \((\neg a)\), \(()\).

Most modern SAT solvers can, in theory at least, polynomially simulate resolution [PipatsrisawatDarwiche2011]. However, it has been proven that some formulas do not have polynomial-size resolution proofs [Haken1985]. For instance, the “pigeon hole formulas”

\[\PHP{p}{h} = (\bigwedge_{i=1}^p(\bigvee_{k=1}^h \PH{i}{k})) \land \bigwedge_{k=1}^h\bigwedge_{1 \le i < j \le p}(\neg \PH{i}{k} \lor \neg \PH{j}{k})\]

where \(\PH{i}{j}\) is true if the pigeon \(i\) sits in the hole \(j\), model all the configurations in which \(p\) pigeons sit in \(h\) holes and each hole has at most pigeon in it. When \(p > h\), the formulas are unsatisfiable. The formulas \(\PHP{p}{p-1}\) do not have polynomial-size resolution proofs.

There are stronger proof systems for which we do not know any formula families that require super-polynomial sized proofs. If no such formula families exists, then \(\NP = \coNP\). Some SAT solvers go beyond resolution and can solve, for instance, pigeon hole problems efficiently.