\(%\usepackage{color}\)
\(%\usepackage{tcolorbox}\)
\(%\tcbuselibrary{skins}\)
\(\usepackage{pifont}\)
\(\)
\(%\definecolor{aaltoblue}{RGB}{00,101,189} % 0065BD\)
\(%\definecolor{aaltored}{RGB}{237,41,57} % ED2939\)
\(\)
\(\definecolor{MyBoxBackground}{rgb}{0.98,0.98,1.0}\)
\(\definecolor{MyBoxBorder}{rgb}{0.90,0.90,1.0}\)
\(%\definecolor{backgroundred}{rgb}{1.0,0.98,0.98}\)
\(%\definecolor{shadowred}{rgb}{1.0,0.90,0.90}\)
\(\)
\(%\newcommand{\subheading}[1]{\textbf{\large\color{fakeaaltobluel}#1}}\)
\(\newcommand{\subheading}[1]{\large{\usebeamercolor[fg]{frametitle}\sc #1}}\)
\(\)
\(\newcommand{\AAccess}[1]{{\footnotesize[\href{https://libproxy.aalto.fi/login?url=#1}{Aalto lib access}]}}\)
\(%\newtcbox{\mybox}[1][red]{on line,arc=0pt,outer arc=0pt,colback=#1!10!white,colframe=#1!50!black,boxsep=0pt,left=1pt,right=1pt,top=2pt,bottom=2pt,boxrule=0pt,bottomrule=1pt,toprule=1pt}\)
\(%\newtcbox{\mybox}[1][MyBoxBackground]{on line,arc=0pt,outer arc=0pt,colback=#1!10!white,colframe=#1!50!black,boxsep=0pt,left=1pt,right=1pt,top=2pt,bottom=2pt,boxrule=0pt,bottomrule=1pt,toprule=1pt}\)
\(\)
\(\newtcolorbox{MyBoxTitled}[1]{colback=MyBoxBackground!100!black,colframe=MyBoxBorder!100!black,boxsep=2pt,left=0pt,right=0pt,top=2pt,bottom=0pt,%enhanced,%\)
\( coltitle=red!25!black,title=#1,boxrule=1pt}\)
\(\)
\(\newtcolorbox{MyBox}[1][]{colback=MyBoxBackground!100!black,colframe=MyBoxBorder!100!black,boxsep=0pt,left=2pt,right=0pt,top=0pt,bottom=0pt,%enhanced,%\)
\( coltitle=red!25!black,boxrule=1pt,#1}\)
\(\)
\(\newenvironment{EqnBox}[1]{\begin{adjustbox}{valign=t}\begin{minipage}{#1}\begin{MyBox}[colback=italyGreen!10!white,colframe=italyGreen!100!black]}{\end{MyBox}\end{minipage}\end{adjustbox}}\)
\(\)
\(\newenvironment{topbox}[1]{\begin{adjustbox}{valign=t}\begin{minipage}{#1}}{\end{minipage}\end{adjustbox}}\)
\(\)
\(\newcommand{\Blue}[1]{{\color{finnishBlue}#1}}\)
\(\newcommand{\Red}[1]{{\color{italyRed}#1}}\)
\(%\newcommand{\Emph}[1]{\emph{\color{aaltoblue}#1}}\)
\(\newcommand{\Emph}[1]{\emph{\usebeamercolor[fg]{structure} #1}}\)
\(%\newcommand{\Emp}{\usebeamercolor[fg]{structure}}\)
\(\newcommand{\Emp}{\color{italyRed}}\)
\(\newcommand{\TextDef}[1]{{\bf\usebeamercolor[fg]{structure} #1}}\)
\(\)
\(\newcommand{\todo}[1]{\textbf{\Red{\Pointer #1}}}\)
\(\newcommand{\TODO}[1]{\todo{#1}}\)
\(\)
\(\newcommand{\Pointer}{\raisebox{-1ex}{\huge\ding{43}}\ }\)
\(\)
\(%\newcommand{\Follows}{\Pointer}\)
\(\newcommand{\Follows}{\color{finnishBlue}\rightsquigarrow}\)
\(\newcommand{\Property}{{\color{italyGreen}\bf Property}}\)
\(\)
\(\)
\(%\)
\(% Common math definitions\)
\(%\)
\(\newcommand{\Set}[1]{\{#1\}}\)
\(\newcommand{\Setdef}[2]{\{{#1}\mid{#2}\}}\)
\(\newcommand{\PSet}[1]{\mathcal{P}(#1)}\)
\(\newcommand{\Pair}[2]{(#1,#2)}\)
\(\newcommand{\Card}[1]{{\vert{#1}\vert}}\)
\(\newcommand{\Tuple}[1]{(#1)}\)
\(\newcommand{\Seq}[1]{[#1]}\)
\(\newcommand{\bbZ}{\mathbb{Z}}\)
\(\newcommand{\Ints}{\mathbb{Z}}\)
\(\newcommand{\Reals}{\mathbb{R}}\)
\(\newcommand{\bbQ}{\mathbb{Q}}\)
\(\newcommand{\Rats}{\bbQ}\)
\(\)
\(\newcommand{\False}{\textsf{F}}\)
\(\newcommand{\True}{\textsf{T}}\)
\(\)
\(\newcommand{\Implies}{\rightarrow}\)
\(\newcommand{\Iff}{\leftrightarrow}\)
\(%\newcommand{\Implies}{\Rightarrow}\)
\(%\newcommand{\Iff}{\Leftrightarrow}\)
\(\newcommand{\Xor}{\oplus}\)
\(\)
\(\newcommand{\Equiv}{\equiv}\)
\(\)
\(\newcommand{\Oh}[1]{O(#1)}\)
\(%\newcommand{\Theta}[1]{\Theta(#1)}\)
\(\)
\(\newcommand{\PHP}[2]{\mathrm{php}_{#1,#2}}\)
\(\newcommand{\PH}[2]{\mathit{x}_{#1,#2}}\)
\(\)
\(\newcommand{\NP}{\textbf{NP}}\)
\(\newcommand{\coNP}{\textbf{co-NP}}\)
\(\)
\(\newcommand{\bnfdef}{\mathrel{\textup{::=}}}\)
\(\newcommand{\bnfor}{\mathrel{\mid}}\)
\(\)
\(\newcommand{\Vars}{X}\)
\(\newcommand{\VarsOf}[1]{\mathop{vars}(#1)}\)
\(\)
\(\newcommand{\Bool}{\Bbb{B}}\)
\(\)
\(\newcommand{\FF}{\bot} % Formula "False"\)
\(\newcommand{\TF}{\top} % Formula "True"\)
\(%\newcommand{\FF}{\mathbf{F}} % Formula "True"\)
\(%\newcommand{\TF}{\mathbf{T}} % Formula "False"\)
\(\)
\(\newcommand{\LHS}{\alpha}\)
\(\newcommand{\RHS}{\beta}\)
\(\newcommand{\EHS}{\gamma}\)
\(\)
\(\newcommand{\Res}[2]{{#1} \otimes {#2}}\)
\(\)
\(\newcommand{\Gates}{{\mathcal G}}\)
\(\newcommand{\Eqns}{{\mathcal D}}\)
\(\newcommand{\Circuit}{{\mathcal C}}\)
\(\newcommand{\GDef}{\mathrel{\mathrm{:=}}}\)
\(\newcommand{\Gate}{g}\)
\(\newcommand{\GateL}{g'}\)
\(\newcommand{\GateR}{g''}\)
\(\newcommand{\GateVar}[1]{v_{#1}}\)
\(\newcommand{\ORf}{\mathbf{or}}\)
\(\newcommand{\ANDf}{\mathbf{and}}\)
\(\newcommand{\NOTf}{\mathbf{not}}\)
\(\newcommand{\OR}[1]{\mathbf{or}(#1)}\)
\(\newcommand{\AND}[1]{\mathbf{and}(#1)}\)
\(\newcommand{\NOT}[1]{\mathbf{not}(#1)}\)
\(\newcommand{\FG}{\mathbf{f}} % Input gate "False"\)
\(\newcommand{\TG}{\mathbf{t}} % Input gate "True"\)
\(\newcommand{\Tseitin}[1]{\mathop{\textrm{cnf}}(#1)}\)
\(\newcommand{\Trans}{\mathrel{\rightsquigarrow}}\)
\(\)
\(\newcommand{\SUD}[3]{x_{#1,#2,#3}}\)
\(\newcommand{\SUDClues}{H}\)
\(\)
\(\newcommand{\PseudoDPLL}{\mathop{\mathit{dpll}}}\)
\(\newcommand{\PseudoAsgn}{\mathrel{\leftarrow}}\)
\(\newcommand{\PseudoUnsat}{\mathbf{unsat}}\)
\(\newcommand{\PseudoSat}{\mathbf{sat}}\)
\(\newcommand{\TA}{\tau}\)
\(\newcommand{\Undef}{\mathit{undef}}\)
\(%\newcommand{\PseudoPropagate}{\textit{propagate}}\)
\(\newcommand{\Asgn}{\leftarrow}\)
\(\newcommand{\PseudoDPLL}{\mathop{\textrm{DPLL}}}\)
\(\newcommand{\PseudoCDCL}{\mathop{\textrm{CDCL}}}\)
\(\newcommand{\PseudoAsgn}{\mathrel{\leftarrow}}\)
\(\newcommand{\PseudoUnsat}{\mathbf{unsat}}\)
\(\newcommand{\PseudoSat}{\mathbf{sat}}\)
\(\newcommand{\PseudoUP}{\mathop{\textit{unit-propagate}}}\)
\(\newcommand{\PseudoAnalyze}{\mathop{\textit{analyze-conflict}}}\)
\(\)
\(%\newcommand{\Neg}[1]{\overline{#1}}\)
\(\newcommand{\Neg}[1]{\neg #1}\)
\(\newcommand{\Vars}{X}\)
\(\newcommand{\VarsOf}[1]{\mathop{vars}(#1)}\)
\(\)
\(\newcommand{\TA}{\tau}\)
\(\newcommand{\Undef}{\mathit{undef}}\)
\(\)
\(%\newcommand{\Form}{\phi}\)
\(\newcommand{\Models}{\models}\)
\(\)
\(\newcommand{\Trail}{\pi}\)
\(\newcommand{\Anno}[2]{#1^{#2}}\)
\(\newcommand{\Lit}{l}\)
\(\newcommand{\Reason}{r}\)
\(\newcommand{\Dec}{\textsf{dec}}\)
\(\)
\(\newcommand{\IG}[1]{G_{#1}}\)
\(\newcommand{\IGVerts}{V}\)
\(\newcommand{\IGEdges}{E}\)
\(\newcommand{\IGEdge}[2]{\Pair{#1}{#2}}\)
\(\newcommand{\IGConflict}{\bot}\)
\(\newcommand{\Cut}{W}\)
\(\)
\(\newcommand{\ResOp}[1]{\mathrel{\otimes_{#1}}}\)
\(\newcommand{\Res}[3]{#1 \ResOp{#3} #2}\)
The DPLL backtracking search procedure
The acronym DPLL stands for “Davis–Putnam–Logemann–Loveland”
by the names of the inventors of the method [DavisPutnam1960] [DavisEtAl1962].
It can be considered as the basic backtracking search approach for solving propositional satisfiability.
The backtracking DPLL search algorithm simply
starts from an empty partial truth assignment,
and
then, recursively, tries both the false and true branches for
an unassigned variable until either
a truth assignment satisfying all the clauses is found, in which case the search terminates, or
a conflict (a falsified clause) is found, in which case the search backtracks to the previous search node.
In pseudocode, one can express the algorithm as follows:
def \( \PseudoDPLL(\phi) \): // \( \phi \) is a CNF formula
return \( \PseudoDPLL(\phi,\emptyset) \)
def \( \PseudoDPLL(\phi,\TA) \): // \( \TA \) is the current partial truth assignment
// A dead-end node?
if \( \phi \) contains a clause falsified by \( \TA \): return \( \PseudoUnsat \)
// Found a satisfying truth assignment?
if \( \TA(x) \) is defined for all \( x \in \VarsOf{\phi} \): return \( (\PseudoSat,\TA) \)
choose a literal \( l \) such that \( \TA(l) \) is undefined
if \( \PseudoDPLL(\phi,\TA \cup \Set{l}) = (\PseudoSat,\TA') \): return \( (\PseudoSat,\TA') \)
if \( \PseudoDPLL(\phi,\TA \cup \Set{\neg{l}}) = (\PseudoSat,\TA') \): return \( (\PseudoSat,\TA') \)
return \( \PseudoUnsat \)
Example
Consider the unsatisfiable CNF formula
\[(a \lor \neg b) \land (\neg a \lor c \lor \neg d) \land (a \lor c \lor \neg d) \land (\neg c \lor \neg e) \land (\neg c \lor e) \land (c \lor d)\]
One search tree for the formula is shown below.
The nodes denote calls to \(\PseudoDPLL\),
the labels next to them describe their partial truth assignments, and
edge labels denote the branching literal.
To save space in figures, we use \(\bar x\) to denote \(\neg x\).
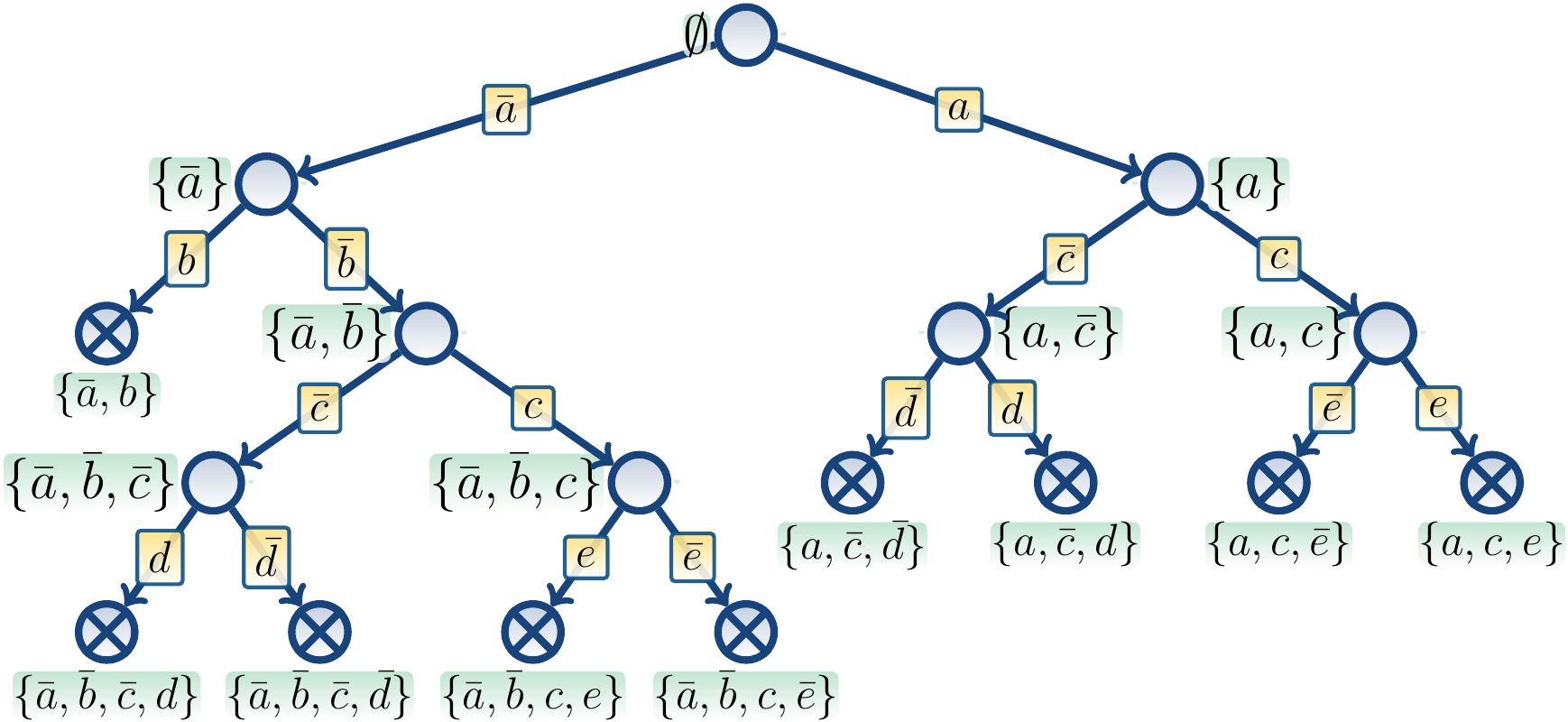
All the search paths end in nodes where at least one clause is falsified,
marked with a cross, and the algorithm returns \(\PseudoUnsat\).
For instance, in the node with the assignment \(\Set{a,\Neg c,\Neg d}\),
the clause \((c \lor d)\) is falsified.
Example
Consider the satisfiable CNF formula
\[(a \lor \neg b) \land (a \lor c \lor \neg d) \land (\neg c \lor \neg e) \land (\neg c \lor e) \land (c \lor d)\]
One search tree for the formula is shown below:
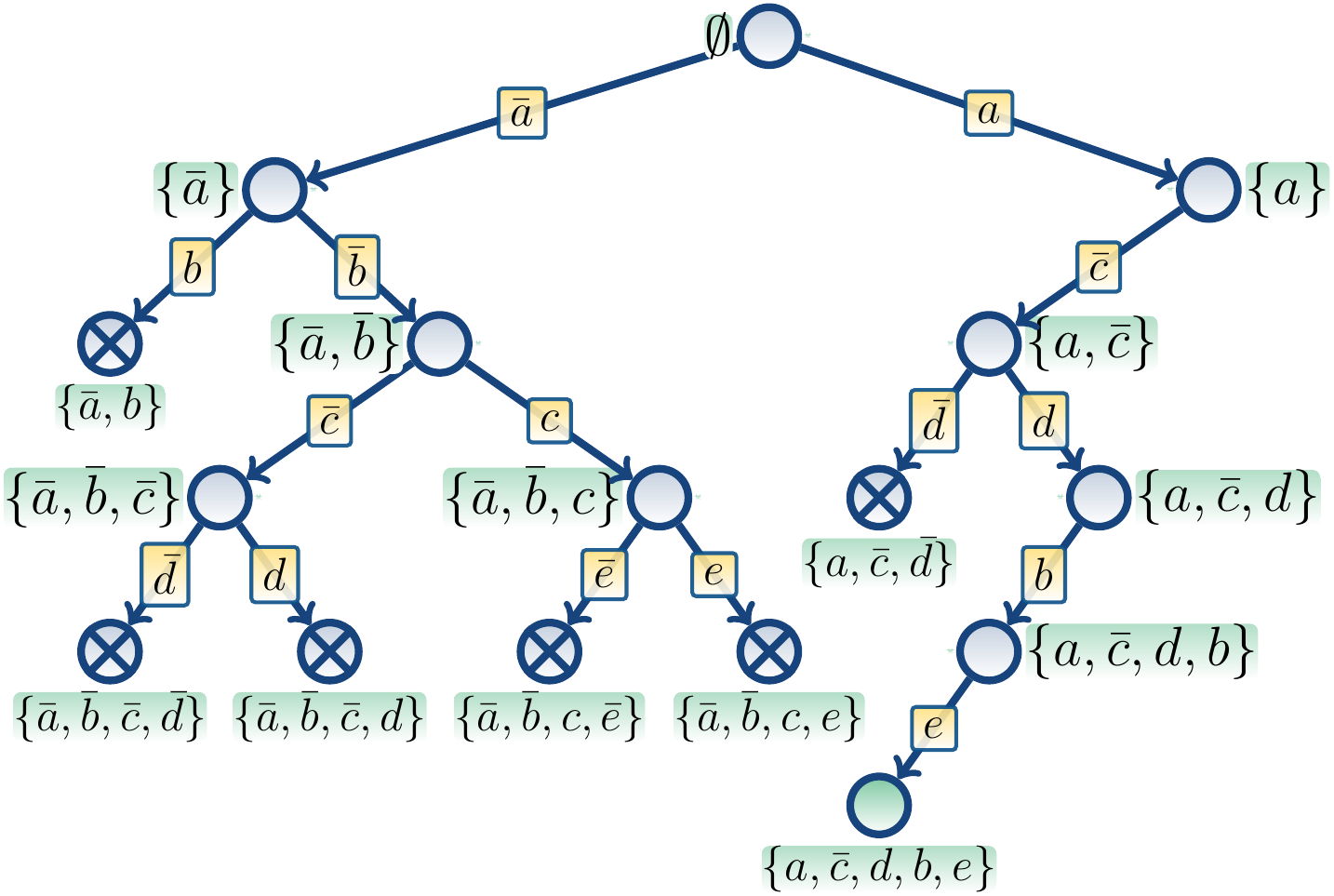
The search is terminated after the node with
the satisfying truth assignment \(\Set{a,b,\Neg c,d,e}\) is reached.
Incorporating unit clause propagation
In practise, one always uses Unit clause propagation to prune the DPLL search space.
One way to incorporate unit propagation in the algorithm is given below
as pseudocode.
def \( \PseudoDPLL(\phi) \): // \( \phi \) is a CNF formula
return \( \PseudoDPLL(\phi,\emptyset) \)
def \( \PseudoDPLL(\phi,\TA) \):
if \( \phi \) contains a clause falsified by \( \TA \): return \( \PseudoUnsat \)
while \( \phi \) contains a unit clause \( C \) in \( \TA \):
\( \TA \PseudoAsgn \TA \cup \Set{l} \), where \( l \) is the literal implied by \( C \)
if \( \phi \) contains a clause falsified by \( \TA \): return \( \PseudoUnsat \)
// Found a satisfying truth assignment?
if \( \TA(x) \) is defined for all \( x \in \VarsOf{\phi} \): return \( (\PseudoSat,\TA) \)
choose a literal \( l \) such that \( \TA(l) \) is undefined
if \( \PseudoDPLL(\phi,\TA \cup \Set{l}) = (\PseudoSat,\TA') \): return \( (\PseudoSat,\TA') \)
if \( \PseudoDPLL(\phi,\TA \cup \Set{\neg l}) = (\PseudoSat,\TA') \): return \( (\PseudoSat,\TA') \)
return \( \PseudoUnsat \)
Example
Consider again unsatisfiable CNF formula
\[(a \lor \neg b) \land (\neg a \lor c \lor \neg d) \land (a \lor c \lor \neg d) \land (\neg c \lor \neg e) \land (\neg c \lor e) \land (c \lor d)\]
If we illustrate the unit clause propagation as out-degree 1 nodes,
then one possible search tree is illustrated below.
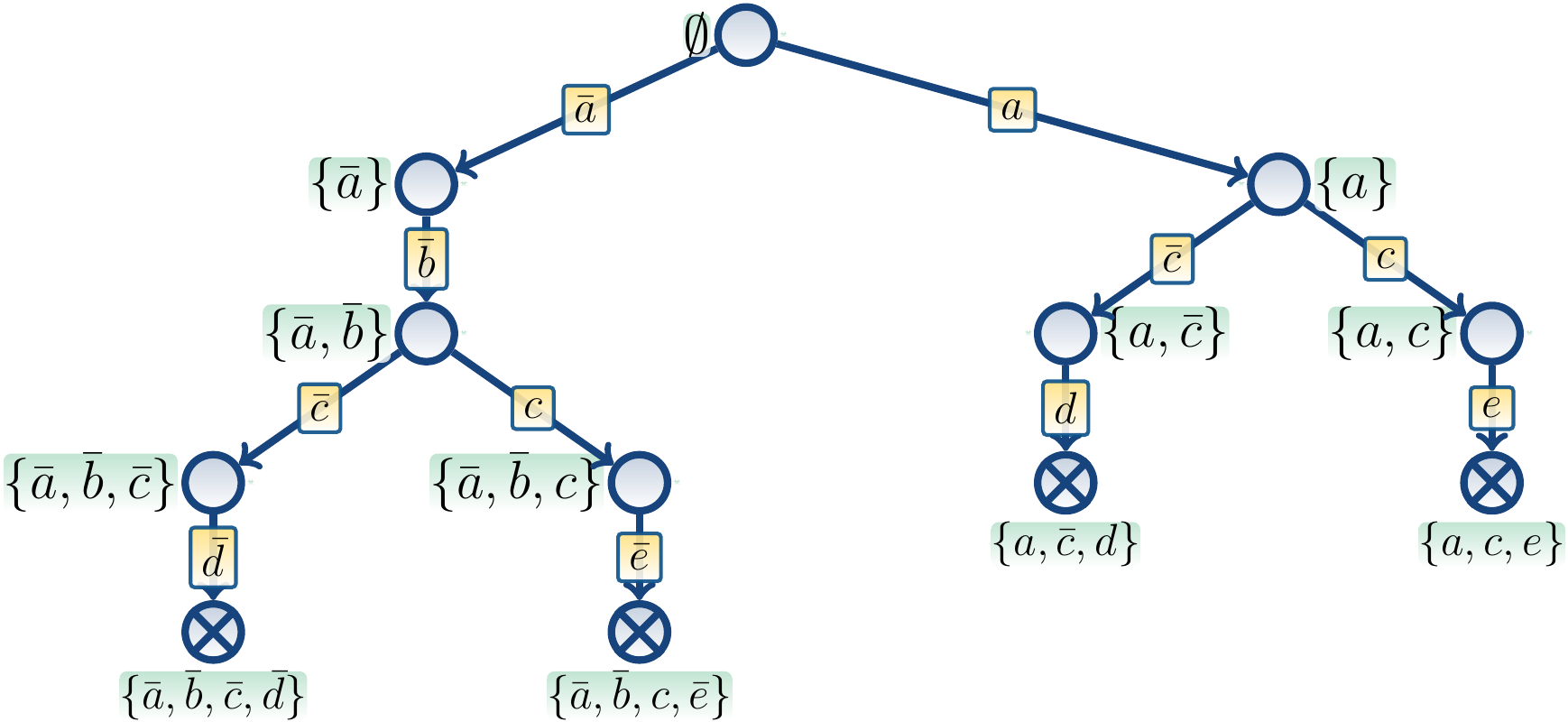
After branching on \(\Neg a\),
unit propagation of the clause \((a \lor \neg b)\) implies \(\Neg b\).
In the resulting node with the truth assignment \(\Set{\Neg a, \Neg b}\),
no further unit clause propagation is possible.
From the node with the truth assignment
\(\Set{\Neg a, \Neg b, \Neg c}\) we obtain \(\Neg d\) by unit
clause propagation on the clause \((a \lor c \lor \Neg d)\).
In the resulting node the clause \((c \lor d)\) is falsified and
the search backtracks.
Unit clause propagation can be “simulated” in the basic version that does not
have it:
the unassigned literal from a unit clause is chosen as the branching literal whenever possible, and thus
the next branch on which the literal is false, will terminate immediately, and
the other next branch will have have the literal set to the correct value.
This simulation will be used in the Section The resolution proof system because we can rather directly derive a proof of unsatisfiability from the basic DPLL search tree.
Example
Consider again unsatisfiable CNF formula
\[(a \lor \neg b) \land (\neg a \lor c \lor \neg d) \land (a \lor c \lor \neg d) \land (\neg c \lor \neg e) \land (\neg c \lor e) \land (c \lor d)\]
The tree below shows the search of the basic version when unit propagation
described in the previous example is simulated with immediately
terminating branches.
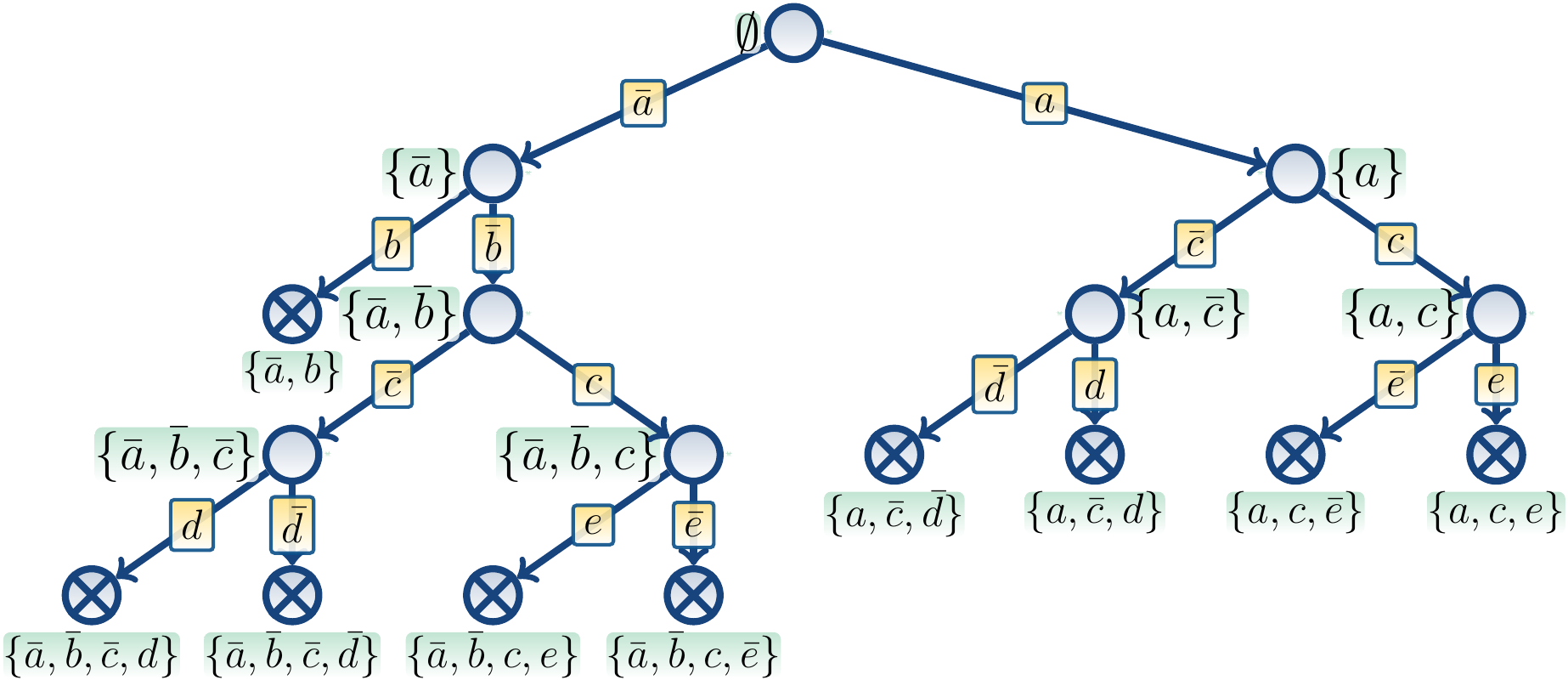
After branching on \(\Neg a\),
unit propagation of the clause \((a \lor \neg b)\)
is shown as the next branch on \(b\) terminating immediately,
effectively forcing \(\Neg b\) to hold.



