Preprocessing¶
Unit clause propagation is relatively efficient in pruning the search space and it can be implemented to work very efficiently by using proper data structures. Thus many SAT solvers use it, and only it, as the constraint propagation technique during the search. However, there are other techniques that could prune the search space in different ways but are considered to be too slow to be used in the inner loop of the search. One alternative for applying such techniques is to use them for preprocessing the formula before the search phase. That is, given a CNF fomula \(\phi\), they are applied to construct another formula \(\phi'\) such that
\(\phi\) is satisfiable if and only if \(\phi'\) is,
from a model of \(\phi'\), it is possible to reconstruct a model for \(\phi\), and
\(\phi'\) is (hopefully) easier to solver that \(\phi\).
Thus they can be seen as transformations that preserves satisfiability and the process of SAT solving with preprocessing is as follows:
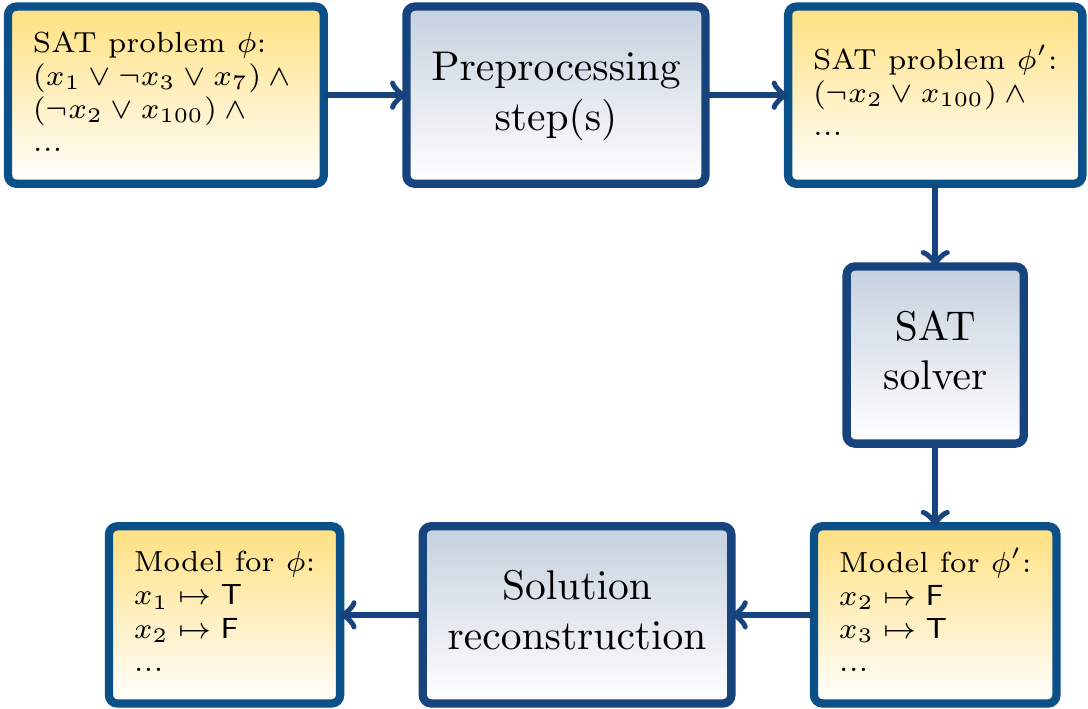
In the CDCL approach, such techniques can also be used interleaved with the search after restarts — in this case, one speaks about “inprocessing”.
In the following, we give examples of some simple preprocessing techniques. Please see, for instance, these slides by Marijn Heule for some other techniques used in modern SAT solvers as well.
Pure literal elimination¶
A literal \(l\) occurring in a CNF formula \(\phi\) is pure if the negated literal \(\Neg{l}\) does not occur in \(\phi\). If \(l\) is pure in \(\phi\), then it is quite easy to see that if \(\TA = \Set{\Neg{l},...}\) satisfies \(\phi\), then so does \(\TA' = (\TA \setminus \Set{\Neg{l}}) \cup \Set{l}\). Therefore, if \(l\) is pure in \(\phi\), one can simplify \(\phi\) by setting \(l\) to true and removing all the clauses in which \(l\) occurs. This is called a pure literal elimination step. The resulting formula is satisfiable if and only \(\phi\) is. Observe that removing clauses can make new pure literals. The pure literal elimination process repeats the pure literal elimination step until the formula no longer has any pure literals.
Example: Pure literal elimination
Consider the formula
The literal \(\Neg{d}\) is pure in \(\phi\). After removing all the clauses with it we get
Now the literal \(c\) is pure and we get the simplified formula
The truth assignment \(\TA_2 = \Set{a, b}\) satisfies the simplied formula \(\phi_2\). Inserting the removed pure literals, we get the truth assignment \(\TA = \Set{a, b, c, \Neg{d}}\) that satisfies the original formula \(\phi\).
Blocked clause elimination¶
Blocked clause elimination [Kullmann1999] is another method for removing “redundant” clauses in a satisfiability-preserving way. We say that a clause \(C\) in a CNF formula \(\phi\) is blocked if \(C\) contains a literal \(l\) such that, for all other clauses \(D\) in \(\phi\), it holds that if \(D\) contains \(\Neg{l}\), then \(D\) also contains another literal \(p\) such that \(C\) contains \(\Neg{p}\). In such a case, we say that \(l\) blocks \(C\) in \(\phi\), and \(l\) is a blocking literal of \(C\) in \(\phi\).
Theorem
If \(C\) is blocked in \(\phi\), then \(\phi\) is satisfiable if and only if \(\phi \setminus \Set{C}\) is satisfiable.
Proof sketch
If a truth assignment \(\TA\) satisfies \(\phi\), then \(\TA\) also satisfies \(\phi \setminus \Set{C}\) because it satisfies all the clauses in \(\phi\) and thus in \(\phi \setminus \Set{C}\).
In the other direction, assume that an assignment \(\TA\) satisfies \(\phi \setminus \Set{C}\) but not \(\phi\). Thus \(\TA\) satisifes all the clauses in \(\phi\) except \(C\). Suppose that the blocking literal of \(C\) is \(l\). Thus \(\TA\) must evaluate \(l\) to false. Let \(\TA'\) be the assignment similar to \(\TA\) except that it evaluates \(l\) to true. Now \(\TA'\) satisfies \(\phi\). We can argue this as follow. Firstly, \(\TA'\) satisfies all the clauses in \(\phi\) that do not involve \(l\) or \(\Neg{l}\) because \(\TA\) does. Secondly, \(\TA'\) obviously satisfies all the clauses in \(\phi\) that contain the literal \(l\). Finally, \(\TA'\) satisfies all the clauses \(D\) in \(\phi\) that contain the literal \(\Neg{l}\) because \(\TA'\) evaluates all the other literals except \(l\) in \(C\) to false and \(D\) must contain the negation of one of these literals by the definition of blocked clauses.
Thus one may remove a blocked clause from \(\phi\) and preserve satisfiability. Observe that if a clause contains a pure literal \(l\), then the clause is blocked because no other clause contains the negated literal \(\Neg{l}\). Thus blocked clause elimination is stronger than pure literal elimination in the sense that it can remove all the clauses that pure literal elimination can and, in many cases, many others as well.
Example
Consider the CNF formula
Observe that the formula has no pure literals and thus pure literal elimination cannot remove any clauses from it. However:
The clause \((a \lor \Neg{b})\) is blocked because for the literal \(a\) in it, only the clause \((\Neg{a} \lor b)\) contains \(\Neg{a}\), and \((\Neg{a} \lor b)\) contains the lietral \(b\) and \((a \lor \Neg{b})\) contains the literal \(\Neg{b}\). We can thus remove the clause \((a \lor \Neg{b})\) and get the formula
\[\phi_1 = (\Neg{a} \lor b) \land (a \lor b \lor c) \land (\Neg{b} \lor \Neg{c})\]Now the clause \((a \lor b \lor c)\) is blocked because for the literal \(b\) in it, the clause \((\Neg{b} \lor \Neg{c})\) with \(\Neg{b}\) contains \(\Neg{c}\) and \((a \lor b \lor c)\) contains its negation \(c\). Removing this blocked clause gives the formula
\[\phi_2 = (\Neg{a} \lor b) \land (\Neg{b} \lor \Neg{c})\]The clause \((\Neg{a} \lor b)\) is now blocked due to the (pure) literal \(\Neg{a}\) and we get the formula
\[\phi_3 = (\Neg{b} \lor \Neg{c})\]Now \((\Neg{b} \lor \Neg{c})\) is blocked because of the (pure) literal \(\Neg{c}\) and, by removing it, we get the trivially satisfiable empty formula.
As the last formula is satisfiable, the original formula is satisfiable as well.
Let’s reconstruct a satisfying truth assignment for the original formula by using the construction described in the proof above. We start from the last formula and select an arbitrary satisfying truth assignment for it; however, we also assign arbitrary values for the variables that appear in the original formula as well. Suppose that we pick the truth assignment \(\TA_1 = \Set{\Neg{a},\Neg{b},\Neg{c}}\) assigning all the variables to false.
The clause \((\Neg{b} \lor \Neg{c})\) was the last one that was removed, due to the blocking literal \(\Neg{c}\). The assignment \(\TA_3\) satisfies the clause \((\Neg{b} \lor \Neg{c})\) and thus the formula \(\phi_3 = (\Neg{b} \lor \Neg{c})\) as well.
The clause \((\Neg{a} \lor b)\) was then the previous one removed, due to the blocking literal \(\Neg{a}\). The assignment \(\TA_2 = \TA_3\) satisties \((\Neg{a} \lor b)\) as well and thus also the formula \(\phi_2 = (\Neg{a} \lor b) \land (\Neg{b} \lor \Neg{c})\).
The clause \((a \lor b \lor c)\) was removed due to the blocking literal \(b\). The assignment \(\TA_2\) does not satisfy the clause and thus we flip the value of the blocking literal \(b\) and obtain the assignment \(\TA_1 = \Set{\Neg{a},b,\Neg{c}}\). Now \(\TA_1\) satisfies not only the clause \((a \lor b \lor c)\) but also the clauses in the formula \(\phi_2\). Therefore, it satisfies the formula \(\phi_1 = (\Neg{a} \lor b) \land (a \lor b \lor c) \land (\Neg{b} \lor \Neg{c})\) as well.
Finally, \(\TA_1 = \Set{\Neg{a},b,\Neg{c}}\) does not satisfy the first removed blocked clause \((a \lor \Neg{b})\). Thus we flip the value of the blocking literal \(a\) and get the assignment \(\TA = \Set{a,b,\Neg{c}}\). This assignment satisfies the clause and all the clauses in \(\phi_1\) and thus the original formula \(\phi\) as well.