A Theory Solver for Equality with Uninterpreted Functions¶

We now present a decision procedure for quantifier-free conjunctions of $ \TEUF $-literals. The explanation is only a high-level sketch; details, optimizations and analysis can be found in the references given later.

Recall that the theory $ \TEUF $ allows arbitrary interpretations for the function symbols as long as they are functions. That is, the function congruence rule $ (v_1 = w_1) \land … \land (v_n = w_n) \Implies f(v_1,…,v_n)=f(w_1,…,w_n) $, where the $ v $’s and $ w $’s are values, must always hold. We can lift this rule to the level of symbolic terms as follows. Assume that we have an equivalence relation $ \UFEq $ over a set of terms. We say that the relation is closed under the function congruence rule if \[(t_1 \UFEq u_1) \land … \land (t_n \UFEq u_n) \Implies f(t_1,…,t_n) \UFEq f(u_1,…,u_n)\] holds whenever $ t_1,…,t_n,u_1,…u_n,f(t_1,…,t_n),f(u_1,…,u_n) $ are terms in the set. If $ (t_1 \UFEq u_1) \land … \land (t_n \UFEq u_n) $ holds but $ f(t_1,…,t_n) \UFNeq f(u_1,…,u_n) $, then we can apply the rule and obtain a new equivalence relation which is the same as $ \UFEq $ except that the classes of $ f(t_1,…,t_n) $ and $ f(u_1,…,u_n) $ are merged.

Example

The equivalence relation $${\UFEq_1} = \Set{\Set{x_1,x_2,x_3},\Set{f(x_1),f(x_3)},\Set{g(x_2,f(x_3))},\Set{g(x_2,f(x_1))}}$$ is not closed under the function congruence rule as $ f(x_1) \UFEq_1 f(x_3) $ but $ g(x_2,f(x_3)) \UFNeq_1 g(x_2,f(x_1)) $. Applying the rule gives the new relation $${\UFEq_2} = \Set{\Set{x_1,x_2,x_3},\Set{f(x_1),f(x_3)},\Set{g(x_2,f(x_3)),g(x_2,f(x_1))}}$$ which is closed under the rule.

The main idea of the algorithm is now quite simple: maintain an equivalence relation over the terms in the formula, and perform the following.

Start with the discrete relation (each term is only equivalent to itself).
When a new equality $ t_1 \Eq t_2 $ are asserted,
1. merge the equivalence classes containing $ t_1 $ and $ t_2 $, and
2. apply the function congruence closure rule until the relation is closed under it.
Remember the asserted disequalities $ t_1 \Neq t_2 $, and check whether they are violated when equivalence classes are merged.

The algorithm and its variants are commonly called the congruence closure algorithm.

Implementing equivalence classes¶

Equivalence classes with merges can be implemented with, e.g., the union-find data structure (recall the Aalto course “CS-A1140 Data Structures and Algorithms”) which maintains the equivalence classes in disjoint trees: two elements are equivalent if they belong to the same tree. To represent the trees, one only needs to associate each element with

a $ \UFRoot $ pointer initialized to point to the element itself, and
a $ \UFRank $, initialized to 0, to keep the constructed tree balanced.

def \( \UFFind{e} \): // Find the root of the tree containing \( e \)
  while \( \UFRootOf{e} \neq e \):
    \( e \Asgn \UFRootOf{e} \)
  return \( e \)

def \( \UFMerge{e_1}{e_2} \): // Merge the classes of \( e_1 \) and \( e_2 \)
  \( r_1 \Asgn \UFFind{e_1} \), \( r_2 \Asgn \UFFind{e_2} \)
  if \( r_1 = r_2 \): return
  if \( \UFRankOf{r_1} < \UFRankOf{r_2} \):
    \( \UFRootOf{r_1} \Asgn r_2 \)
  else if \( \UFRankOf{r_1} > \UFRankOf{r_2} \):
    \( \UFRootOf{r_2} \Asgn r_1 \)
  else:
    \( \UFRootOf{r_1} \Asgn r_2 \)
    \( \UFRankOf{r_2} \Asgn \UFRankOf{r_2}+1 \)
 

Example

Assume the elements $ e_1,…,e_5 $.

Initially, each element is in its own class. Thus $ e_i \UFEqNot e_j $ whenever $ i \neq j $.
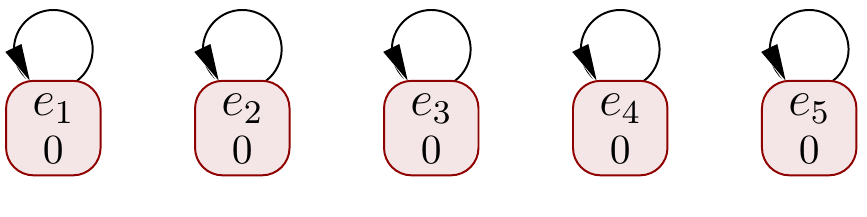
Execute $ \UFMerge{e_1}{e_2} $.
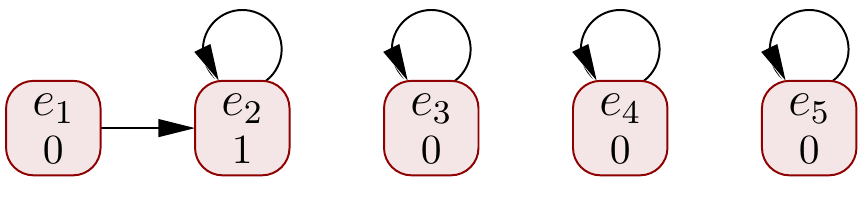
Execute $ \UFMerge{e_5}{e_4} $
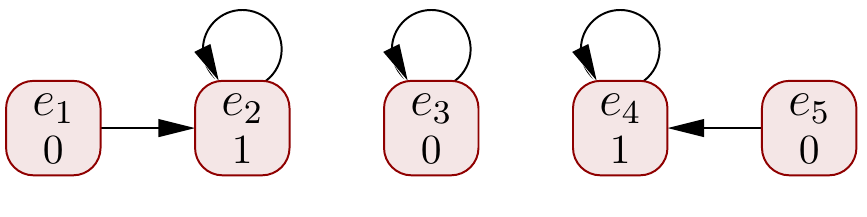
Execute $ \UFMerge{e_1}{e_5} $

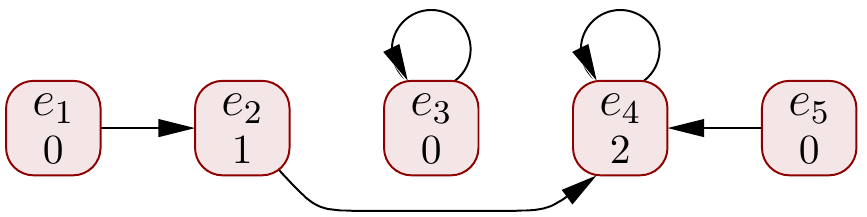
Now $ \UFFind{e_1} = e_4 = \UFFind{e_5} $ and thus $ e_1 \UFEq e_5 $.

Asserting equality and disequality atoms¶

The core part of our $ \TEUF $-solver is to maintain the equivalence classes between the terms, and their sub-terms, when equalities and disequalities are asserted. Initially, each term is in its own equivalence class. When an equality between two terms is asserted, the algorithm

merges the corresponding classes,
applies the congruence rule until the equivalence relation becomes closed under it, and
checks if a recorded disequality is violated.

When a disequality between two terms is asserted, the solver

checks if the terms are equivalent, and
records the disequality.

def \( \SMTAssert{t \Eq u} \):
  \( \CCPending \Asgn \Set{\Pair{t}{u}} \)
  while \( \CCPending \) not empty:
    pop a \( \Pair{v}{w} \) from \( \CCPending \)
    if \( \UFFind{v}=\UFFind{w} \): continue
    \( \UFMerge{v}{w} \)
    for each pair \( v' \), \( w' \) such that
       1. \( v' \Abbrv f(v'_1,...,v'_n) \) and \( w' \Abbrv f(w'_1,...,w'_n) \),
       2. \( \UFFind{v'_1}=\UFFind{w'_1},..., \)
          \( \UFFind{v'_n}=\UFFind{w'_n} \), and
       3. \( \UFFind{v'} \neq \UFFind{w'} \),
      add \( \Pair{v'}{w'} \) in \( \CCPending \)
  for each recorded \( v \Neq w \):
    if \( \UFFind{v}=\UFFind{w} \): return false
  return true

def \( \SMTAssert{\neg(t \Eq u)} \):
  if \( \UFFind{t}=\UFFind{u} \): return false
  record \( t \Neq u \)
  return true
 

Example

Consider the conjunction \[{f(f(f(x))) \Eq x} \land {f(f(f(f(f(x))))) \Eq x} \land {f(x) \Neq x}\] and, for clarity, use the abbreviations $ t_1 \Abbrv f(x) $, $ t_2 \Abbrv f(f(x)) \Abbrv f(t_1) $, $ t_3 \Abbrv f(t_2) $, $ t_4 \Abbrv f(t_3) $, $ t_5 \Abbrv f(t_4) $ for the component terms. The parse tree of the formula can be drawn as

Initially, the equivalence classes are $ \Set{x},\Set{t_1},\Set{t_2},\Set{t_3},\Set{t_4},\Set{t_5} $ and the union-find data structure looks like
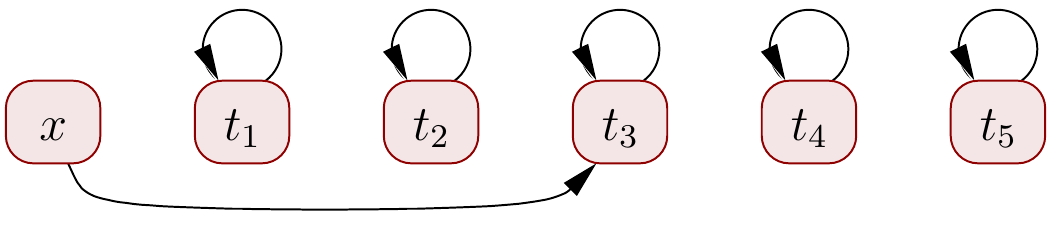
Asserting $ f(f(f(x))) \Eq x $ merges $ t_3 $ and $ x $: $ \Set{x,t_3},\Set{t_1},\Set{t_2},\Set{t_4},\Set{t_5} $
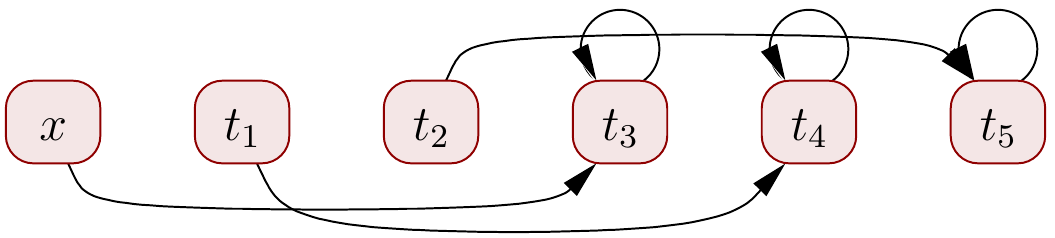
$ x \UFEq t_3 $ implies $ {t_1 \Abbrv f(x)} \UFEq {t_4 \Abbrv f(t_3)} $: $ \Set{x,t_3},\Set{t_1,t_4},\Set{t_2},\Set{t_5} $
$ t_1 \UFEq t_4 $ implies $ {t_2 \Abbrv f(t_1)} \UFEq {t_5 \Abbrv f(t_4)} $: $ \Set{x,t_3},\Set{t_1,t_4},\Set{t_2,t_5} $
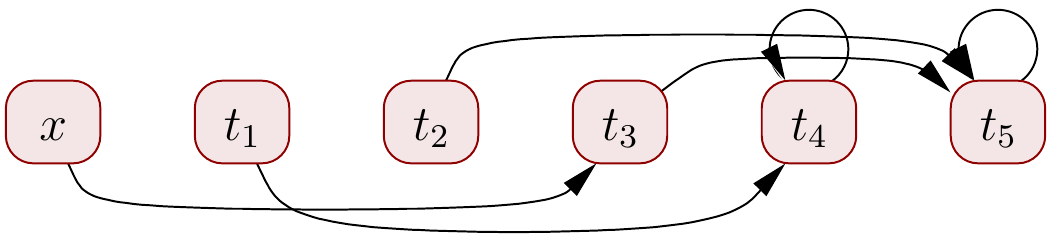
Asserting $ f(f(f(f(f(x))))) \Eq x $ merges $ t_5 $ and $ x $: $ \Set{x,t_3,t_2,t_5},\Set{t_1,t_4} $
$ x \UFEq t_2 $ implies $ t_1 = f(x) \UFEq t_3=f(t_2) $: $ \Set{x,t_3,t_2,t_5,t_1,t_4} $
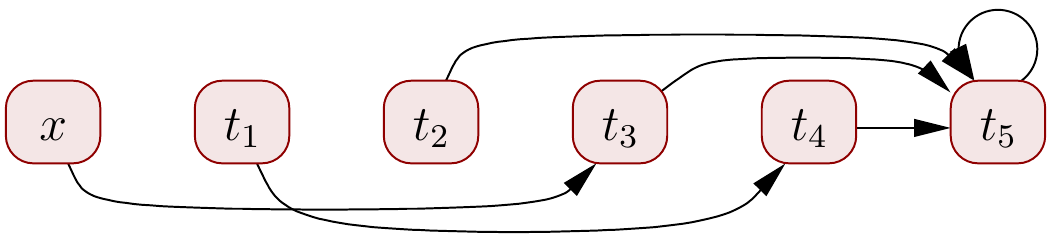
Now we see that $ {t_1 \Abbrv f(x)} \UFEq x $ and thus $ f(x) \Eq x $ should hold. However, $ f(x) \Neq x $ is a conjunct in the original conjunction and therefore the conjunction is unsatisfiable.

When actually implementing the above methods, (i) the equivalence classes can be implemented with the union-find data structure, (ii) finding congruent terms can be implemented with a hash table, and (iii) backtracking equals to undoing the merges (and recomputing hash values).

When a conjunction is satisfiable, constructing a model for it is easy: just assign the elements in each equivalence class into a distinct value.

Theory-Implied Literals¶

Propagation of positive atoms $ t_1 \Eq t_2 $ is fast:

at each merge, check if $ t_1 $ and $ t_2 $ are merged to the same class
if yes, report $ t_1 \Eq t_2 $ as an implied literal.

Propagating negative literals requires more work:

When asserting $ \neg(t_1 \Eq t_2) $ and $ t_1 \UFEqNot t_2 $ holds, report, for each atom $ t’_1 \Eq t’_2 $ with $ t’_1 \UFEq t_1 $ and $ t’_2 \UFEq t_2 $, the implied literal $ \neg(t’_1 \Eq t’_2) $
When merging two classes, find atoms of form $ t’_1 \Eq t’_2 $ for which (i) $ t’_1 $ or $ t’_2 $ are in the merged class, and (ii) $ t’_1 \UFEq t_1 $ and $ t’_2 \UFEq t_2 $ hold for some recorded disequality $ t_1 \Neq t_2 $, and report the implied literal $ \neg(t’_1 \Eq t’_2) $.

Example

Consider the formula \[\neg({x \Eq y} \land {y \Eq z}) \land ({y \Eq f(z)} \Implies {g(x) \Eq g(f(z))} \land {z \Eq f(z)})\] Initially all its terms are in their own equivalence classes and $ {\UFEq_0} = \Set{\Set{x},\Set{g(x)},\Set{y},\Set{z},\Set{f(z)},\Set{g(f(z))}} $. Consider the following sequence of literal assertions

The CDCL SAT solver asserts $ x \Eq y $ into the theory solver, which updates the equivalence relation to $ {\UFEq_1} = \Set{\Set{x,y},\Set{g(x)},\Set{z},\Set{f(z)},\Set{g(f(z))}} $.
The CDCL SAT solver asserts $ \neg(y \Eq z) $ into to theory solver, which does not update the equivalence relation but records the disequality. Note that $ \neg(x \Eq z) $ would be implied at this point if it were an atom in the formula.
The CDCL SAT solver asserts $ y \Eq f(z) $ into the theory solver, which updates the equivalence relation to $ {\UFEq_2} = \Set{\Set{x,y,f(z)},\Set{g(x),g(f(z))},\Set{z}} $. Note that as $ x $ and $ f(z) $ are in the same class, the classes of $ g(x) $ and $ g(f(z)) $ are merged as well.
The theory solver reports the implied literals
1. $ g(x) \Eq g(f(z)) $, and
2. $ \neg(z \Eq f(z)) $ as $ f(z) \UFEq_2 y $ and $ \neg(y \Eq z) $ is recorded.

To produce explanations, one can remember in a “reason graph”

each equality and disequality assertion, and
for each implied literal, the immediate reason for the implication.

The reasons can then be recursively expanded to get the explanation consisting only of assertions.

Example: Continues the previous one

For the previous example, the reason graph could be

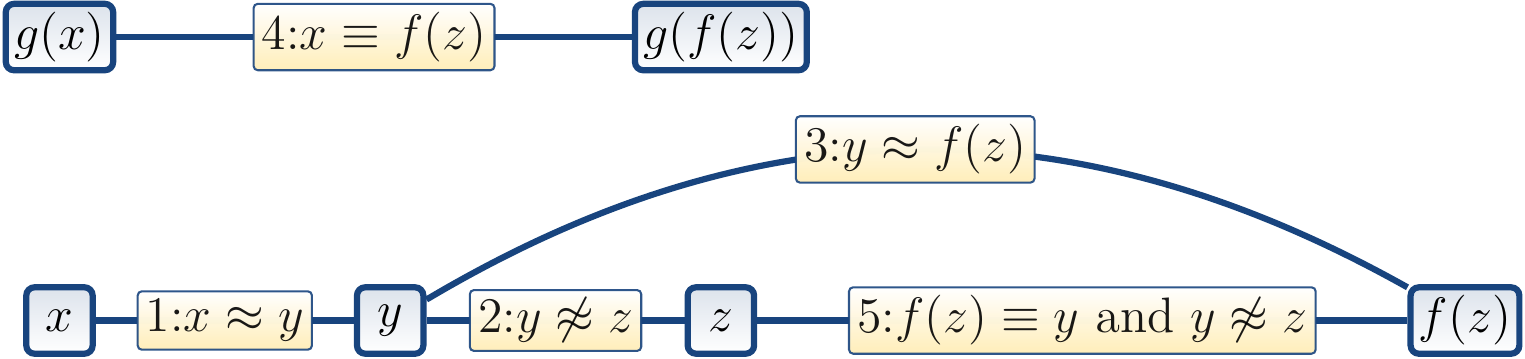
The explanation for $ g(x) \Eq g(f(z)) $ is obtained by explaining the immediate reason $ x \UFEq f(z) $. This is done by explaining the path between $ x $ and $ f(z) $. The result is $ (x \Eq y) \land (y \Eq f(z)) $.

The explanation for $ \neg(z \Eq f(z)) $ is $ y \Neq z $ conjuncted with the explanation for $ f(z) \UFEq y $, i.e., the assertion $ y \Eq f(z) $.

Some further reading¶

Classic papers on congruence closure:

R. Shostak: An Algorithm for Reasoning About Equality, Commun. ACM 21(7):583–585, 1978
P. Downey, R. Sethi, R. Tarjan: Variations on the Common Subexpression Problem, J. ACM 27(4):758–771, 1980
G. Nelson, D. Oppen: Fast Decision Procedures Based on Congruence Closure, J. ACM 27(2):356–364, 1980

A contemporary approach giving fast algorithms for congruence closure as well as an extension to integer offsets, allowing atoms of form $ x = y + k $ for integer constants $ k $:

R. Nieuwenhuis and A. Oliveras: Fast congruence closure and extensions, Inform. and Comput. 205(4), pp. 557–580, 2007

Congruence closure in a theorem proving setting:

L. Bachmair, A. Tiwari, L. Vigneron: Abstract Congruence Closure, J. Automated Reasoning 31(2):129–168, 2003