\(%\usepackage{color}\)
\(%\usepackage{tcolorbox}\)
\(%\tcbuselibrary{skins}\)
\(\usepackage{pifont}\)
\(\)
\(\definecolor{fakeaaltobluel}{RGB}{00,141,229} % 0065BD\)
\(\definecolor{aaltoblue}{RGB}{00,101,189} % 0065BD\)
\(\definecolor{aaltored}{RGB}{237,41,57} % ED2939\)
\(\)
\(\definecolor{MyBoxBackground}{rgb}{0.98,0.98,1.0}\)
\(\definecolor{MyBoxBorder}{rgb}{0.90,0.90,1.0}\)
\(\definecolor{backgroundred}{rgb}{1.0,0.98,0.98}\)
\(\definecolor{shadowred}{rgb}{1.0,0.90,0.90}\)
\(\)
\(%\newcommand{\subheading}[1]{\textbf{\large\color{fakeaaltobluel}#1}}\)
\(\newcommand{\subheading}[1]{\large{\usebeamercolor[fg]{frametitle} #1}}\)
\(\)
\(\)
\(%\newtcbox{\mybox}[1][red]{on line,arc=0pt,outer arc=0pt,colback=#1!10!white,colframe=#1!50!black,boxsep=0pt,left=1pt,right=1pt,top=2pt,bottom=2pt,boxrule=0pt,bottomrule=1pt,toprule=1pt}\)
\(%\newtcbox{\mybox}[1][MyBoxBackground]{on line,arc=0pt,outer arc=0pt,colback=#1!10!white,colframe=#1!50!black,boxsep=0pt,left=1pt,right=1pt,top=2pt,bottom=2pt,boxrule=0pt,bottomrule=1pt,toprule=1pt}\)
\(\)
\(\newtcolorbox{MyBoxTitled}[1]{colback=MyBoxBackground!100!black,colframe=MyBoxBorder!100!black,boxsep=2pt,left=0pt,right=0pt,top=2pt,bottom=0pt,%enhanced,%\)
\( coltitle=red!25!black,title=#1,boxrule=1pt}\)
\(\)
\(\newtcolorbox{MyBox}[1][]{colback=MyBoxBackground!100!black,colframe=MyBoxBorder!100!black,boxsep=0pt,left=2pt,right=0pt,top=0pt,bottom=0pt,%enhanced,%\)
\( coltitle=red!25!black,boxrule=1pt,#1}\)
\(\)
\(\newenvironment{EqnBox}[1]{\begin{adjustbox}{valign=t}\begin{minipage}{#1}\begin{MyBox}[colback=backgroundred!100!black,colframe=shadowred!100!black]}{\end{MyBox}\end{minipage}\end{adjustbox}}\)
\(\)
\(\newenvironment{topbox}[1]{\begin{adjustbox}{valign=t}\begin{minipage}{#1}}{\end{minipage}\end{adjustbox}}\)
\(\)
\(\newcommand{\Blue}[1]{{\color{aaltoblue}#1}}\)
\(\newcommand{\Red}[1]{{\color{aaltored}#1}}\)
\(%\newcommand{\Emph}[1]{\emph{\color{aaltoblue}#1}}\)
\(\newcommand{\Emph}[1]{\emph{\usebeamercolor[fg]{structure} #1}}\)
\(\newcommand{\TextDef}[1]{{\bf\usebeamercolor[fg]{structure} #1}}\)
\(\)
\(\newcommand{\todo}[1]{\textbf{\Red{\Pointer #1}}}\)
\(\newcommand{\TODO}[1]{\todo{#1}}\)
\(\)
\(\newcommand{\Pointer}{\raisebox{-1ex}{\huge\ding{43}}\ }\)
\(\)
\(\)
\(%\)
\(% Common math definitions\)
\(%\)
\(\newcommand{\Set}[1]{\{#1\}}\)
\(\newcommand{\Setdef}[2]{\{{#1}\mid{#2}\}}\)
\(\newcommand{\PSet}[1]{\mathcal{P}(#1)}\)
\(\newcommand{\Pair}[2]{(#1,#2)}\)
\(\newcommand{\Card}[1]{{\vert{#1}\vert}}\)
\(\newcommand{\Tuple}[1]{(#1)}\)
\(\newcommand{\Seq}[1]{[#1]}\)
\(\newcommand{\bbZ}{\mathbb{Z}}\)
\(\newcommand{\Ints}{\mathbb{Z}}\)
\(\newcommand{\Reals}{\mathbb{R}}\)
\(\newcommand{\bbQ}{\mathbb{Q}}\)
\(\newcommand{\Rats}{\bbQ}\)
\(\newcommand{\bbN}{\mathbb{N}}\)
\(\newcommand{\Nats}{\bbN}\)
\(\)
\(\newcommand{\Floor}[1]{\lfloor #1 \rfloor}\)
\(\newcommand{\Ceil}[1]{\lceil #1 \rceil}\)
\(\)
\(\newcommand{\False}{\textsf{F}}\)
\(\newcommand{\True}{\textsf{T}}\)
\(\)
\(\newcommand{\Implies}{\rightarrow}\)
\(\newcommand{\Iff}{\leftrightarrow}\)
\(%\newcommand{\Implies}{\Rightarrow}\)
\(%\newcommand{\Iff}{\Leftrightarrow}\)
\(\newcommand{\Xor}{\oplus}\)
\(\)
\(\newcommand{\Equiv}{\equiv}\)
\(\)
\(\newcommand{\Oh}[1]{O(#1)}\)
\(%\newcommand{\Theta}[1]{\Theta(#1)}\)
\(\)
\(\newcommand{\PHP}[2]{\mathrm{php}_{#1,#2}}\)
\(\newcommand{\PH}[2]{\mathit{x}_{#1,#2}}\)
\(\)
\(\newcommand{\NP}{\textbf{NP}}\)
\(\newcommand{\coNP}{\textbf{co-NP}}\)
\(\)
\(\newcommand{\bnfdef}{\mathrel{\textup{::=}}}\)
\(\newcommand{\bnfor}{\mathrel{\mid}}\)
\(\)
\(\newcommand{\Def}{\mathrel{:=}}\)
\(\)
\(\newcommand{\LSF}{\alpha}\)
\(\newcommand{\RSF}{\beta}\)
\(\newcommand{\SF}{\phi}\)
\(\newcommand{\MF}{\gamma}\)
\(%\newcommand{\Abbrv}{\equiv}\)
\(\newcommand{\Abbrv}{\Def}\)
\(\newcommand{\AbbrvEq}{\equiv}\)
\(\newcommand{\Exists}[2]{\exists{#1}.\,#2}\)
\(%\newcommand{\E}[3]{\exists{#1{:}#2}.\,#3}\)
\(\newcommand{\E}[3]{\exists{#1{:}\,#3}}\)
\(\newcommand{\Forall}[2]{\forall{#1}.\,#2}\)
\(%\newcommand{\Furall}[3]{\forall{#1{:}#2}.\,#3}\)
\(%\newcommand{\A}[3]{\forall{#1{:}#2}.\,#3}\)
\(\newcommand{\A}[3]{\forall{#1{:}\,#3}}\)
\(\newcommand{\Models}{\models}\)
\(\newcommand{\NotModels}{\not\models}\)
\(\)
\(\newcommand{\Substf}[3]{#1[#2 \mapsto #3]}\)
\(\newcommand{\Functions}[2]{[#1 \to #2]}\)
\(\)
\(\)
\(\newcommand{\Eq}{\approx}\)
\(\newcommand{\EqS}[1]{\approx_{#1}}\)
\(\newcommand{\Neq}{\not\approx}\)
\(\)
\(%\newcommand{\Th}{\mathcal{T}}\)
\(\newcommand{\Th}{T}\)
\(\newcommand{\ThI}[1]{\Th_{#1}}\)
\(\)
\(\newcommand{\Sig}{\Sigma}\)
\(\newcommand{\SigI}[1]{\Sigma_{#1}}\)
\(\newcommand{\Interp}{I}\)
\(%\newcommand{\Interp}{{\mathcal{I}}}\)
\(\newcommand{\InterpOf}[1]{#1^\Interp}\)
\(\newcommand{\InterpIOf}[2]{#2^{#1}}\)
\(\newcommand{\InterpRestr}[1]{\Interp^{#1}}\)
\(\newcommand{\InterpI}[1]{I_{#1}}\)
\(%\newcommand{\InterpI}[1]{{\mathcal{I}_{#1}}}\)
\(%\newcommand{\InterpIOf}[2]{#2^{\InterpI{#1}}}\)
\(\newcommand{\InterpDom}{D_{\Interp}}\)
\(\newcommand{\InterpSubst}[2]{\Interp[{#1}\mapsto{#2}]}\)
\(\newcommand{\ThModels}{\mathrel{\models_{\Th}}}\)
\(\newcommand{\ThIModels}[1]{\mathrel{\models_{\ThI{#1}}}}\)
\(\)
\(% Example interpretations\)
\(\newcommand{\IInts}{\InterpI{\textrm{ints}}}\)
\(\newcommand{\IIntsOf}[1]{\InterpIOf{\IInts}{#1}}\)
\(\newcommand{\IMods}{\InterpI{\textrm{mod7}}}\)
\(\newcommand{\IModsOf}[1]{\InterpIOf{\IMods}{#1}}\)
\(\newcommand{\ISilly}{\InterpI{\textrm{silly}}}\)
\(\newcommand{\ISillyOf}[1]{\InterpIOf{\ISilly}{#1}}\)
\(\)
\(\)
\(%\newcommand{\El}[1]{\textup{e}_{#1}}\)
\(\)
\(\newcommand{\ElemI}{\textup{\ding{40}}}\)
\(\newcommand{\ElemII}{\textup{\ding{41}}}\)
\(\newcommand{\ElemIII}{\textup{\ding{46}}}\)
\(\)
\(\newcommand{\ElemA}{\circ}\)
\(\newcommand{\ElemB}{\bullet}\)
\(\)
\(\newcommand{\AxiomMarg}[1]{\makebox{}\hfill(\Blue{#1})}\)
\(\newcommand{\Comment}[1]{\makebox{}\hfill\Blue{#1}}\)
\(\)
\(\newcommand{\DLZ}{\mathit{DL}(\bbZ)}\)
\(\newcommand{\DLQ}{\mathit{DL}(\bbQ)}\)
\(\newcommand{\EUF}{\mathit{EUF}}\)
\(\newcommand{\TEUF}{\ThI{\mathit{EUF}}}\)
\(\newcommand{\LIA}{\mathit{LIA}}\)
\(\newcommand{\TLIA}{\ThI{\mathit{LIA}}}\)
\(\newcommand{\TNRA}{\ThI{\mathit{NRA}}}\)
\(\newcommand{\TNIA}{\ThI{\mathit{NIA}}}\)
\(\newcommand{\LRA}{\mathit{LRA}}\)
\(\newcommand{\TLRA}{\ThI{\mathit{LRA}}}\)
\(\newcommand{\IDL}{\mathit{IDL}}\)
\(\newcommand{\RDL}{\mathit{RDL}}\)
\(\newcommand{\EUFModels}{\mathrel{\models_{\TEUF}}}\)
\(\newcommand{\EUFModelsNot}{\mathrel{{\not\models}_{\TEUF}}}\)
\(\newcommand{\LIAModels}{\mathrel{\models_{\LIA}}}\)
\(\newcommand{\LIANotModels}{\mathrel{\not\models_{\LIA}}}\)
\(\newcommand{\LIAEntails}{\mathrel{\models_{\LIA}}}\)
\(\newcommand{\IDLEntails}{\mathrel{\models_{\IDL}}}\)
\(\newcommand{\NIAModels}{\mathrel{\models_{\TNIA}}}\)
\(\newcommand{\Div}[2]{{{#1}\mid{#2}}}\)
\(\)
\(\newcommand{\Sort}{s}\)
\(\newcommand{\SortI}[1]{s_{#1}}\)
\(\newcommand{\Sorts}{S}\)
\(\newcommand{\Func}{f}\)
\(\newcommand{\Funcs}{F}\)
\(\newcommand{\Pred}{p}\)
\(\newcommand{\Preds}{P}\)
\(\newcommand{\SortName}[1]{\textsf{#1}}\)
\(\)
\(\newcommand{\Var}{x}\)
\(\newcommand{\Vars}{X}\)
\(\newcommand{\BVar}{a}\)
\(\newcommand{\BVars}{\mathcal{B}}\)
\(\newcommand{\Val}{v}\)
\(\)
\(\newcommand{\DomOf}[1]{D_{#1}}\)
\(\)
\(\newcommand{\Term}{t}\)
\(\newcommand{\TermI}[1]{t_{#1}}\)
\(\newcommand{\TermP}[1]{t'}\)
\(\newcommand{\Atom}{A}\)
\(\)
\(\)
\(%\)
\(% EUF\)
\(%\)
\(\newcommand{\UFEq}{\equiv}\)
\(\newcommand{\UFEqP}{\mathrel{\equiv'}}\)
\(\newcommand{\UFEqNot}{\not\equiv}\)
\(\newcommand{\UFNeq}{\not\equiv}\)
\(\)
\(\)
\(\)
\(%\)
\(% Arithmetics\)
\(%\)
\(\newcommand{\IntsSort}{\textrm{Int}}\)
\(\newcommand{\IntsSig}{\SigI{\textrm{Int}}}\)
\(\newcommand{\RealsSort}{\textrm{Real}}\)
\(\newcommand{\Mul}{\mathbin{*}}\)
\(\)
\(%\)
\(% Arrays\)
\(%\)
\(\newcommand{\IndexSort}{\SortName{idx}}\)
\(%\newcommand{\IndexSort}{\SortName{index}}\)
\(\newcommand{\ElemSort}{\SortName{elem}}\)
\(%\newcommand{\ArraySort}{\SortName{array}}\)
\(\newcommand{\ArraySort}{\SortName{arr}}\)
\(\newcommand{\ArrSig}{\Sigma_{\mathit{arrays}}}\)
\(\newcommand{\ArrE}[1]{\textrm{a}_{#1}}\)
\(\)
\(\)
\(\newcommand{\TArrays}{\ThI{\mathit{arrays}}}\)
\(\newcommand{\TArraysExt}{\ThI{\mathit{arrays}}^{=}}\)
\(\newcommand{\ArrModels}{\mathrel{{\models_\mathit{arrays}}}}\)
\(\)
\(\)
\(%\)
\(% Theories of Lisp-like lists\)
\(%\)
\(\newcommand{\ThCons}{\ThI{\textrm{cons}}}\)
\(\newcommand{\ThConsAcyclic}{\ThI{\textrm{cons+}}}\)
\(\newcommand{\SigCons}{\SigI{\textrm{cons}}}\)
\(\newcommand{\Cons}{\FuncName{cons}}\)
\(\newcommand{\Car}{\FuncName{car}}\)
\(\newcommand{\Cdr}{\FuncName{cdr}}\)
\(\newcommand{\LAtom}{\PredName{atom}}\)
\(% Sorted version additions\)
\(\newcommand{\ListSort}{\SortName{list}}\)
\(\newcommand{\Nil}{\FuncName{nil}}\)
\(\newcommand{\Length}{\FuncName{length}}\)
\(\)
\(\)
\(\newcommand{\BVT}{\ThI{\mathsf{BV}}}\)
\(\newcommand{\BVSig}{\SigI{\mathsf{BV}}}\)
\(\newcommand{\BVS}[1]{\SortName{[}#1\SortName{]}}\)
\(%\newcommand{\BVS}[1]{[{#1}]}\)
\(\newcommand{\BVAdd}[1]{\mathbin{{+}_{\BVS{#1}}}}\)
\(\newcommand{\BVLE}[1]{\mathbin{{\le}_{\BVS{#1}}}}\)
\(\newcommand{\BVGE}[1]{\mathbin{{\ge}_{\BVS{#1}}}}\)
\(\newcommand{\BVSL}[1]{\mathbin{{\ll}_{\BVS{#1}}}}\)
\(\newcommand{\BVTermB}[1]{\hat{t}_{(#1)}}\)
\(%\newcommand{\BVTermBI}[2]{\hat{t}_{#1}^{(#2)}}\)
\(\newcommand{\BVAtom}{\hat{A}}\)
\(\newcommand{\BVXB}[1]{\hat{x}_{(#1)}}\)
\(\newcommand{\BVYB}[1]{\hat{y}_{(#1)}}\)
\(\newcommand{\BVVar}[1]{\hat{x}_{(#1)}}\)
\(\)
\(\)
\(% SMTLIB logics\)
\(\newcommand{\SMTLIBLogic}[1]{\textrm{#1}}\)
\(\newcommand{\QFUF}{\SMTLIBLogic{QF\_UF}}\)
\(\newcommand{\QFLIA}{\SMTLIBLogic{QF\_LIA}}\)
\(\newcommand{\QFUFLRA}{\SMTLIBLogic{QF\_UFLRA}}\)
\(\newcommand{\SMTLIBLIA}{\SMTLIBLogic{LIA}}\)
\(\)
\(\newcommand{\CG}[1]{G_{#1}}\)
\(\newcommand{\DiffEdge}[1]{\overset{#1}{\longrightarrow}}\)
\(\)
\(\newcommand{\FuncName}[1]{\textsf{#1}}\)
\(\newcommand{\PredName}[1]{\textsf{#1}}\)
\(\newcommand{\ReadF}{\FuncName{read}}\)
\(\newcommand{\Read}[2]{\ReadF(#1,#2)}\)
\(\newcommand{\WriteF}{\FuncName{write}}\)
\(\newcommand{\Write}[3]{\WriteF(#1,#2,#3)}\)
\(\)
\(\newcommand{\Abs}[1]{\alpha_{#1}}\)
\(\)
\(\newcommand{\Expl}[1]{\textit{explain}(#1)}\)
\(\)
\(\newcommand{\SMTAssertF}{\textsf{assert}}\)
\(\newcommand{\SMTAssert}[1]{\SMTAssertF(#1)}\)
\(\)
\(\newcommand{\UFRoot}{\textit{parent}}\)
\(\newcommand{\UFRootOf}[1]{{#1}.\UFRoot}\)
\(\newcommand{\UFRank}{\textit{rank}}\)
\(\newcommand{\UFRankOf}[1]{{#1}.\UFRank}\)
\(\newcommand{\UFFind}[1]{\textsf{find}(#1)}\)
\(\newcommand{\UFMerge}[2]{\textsf{merge}(#1,#2)}\)
\(\)
\(\newcommand{\CCPending}{\textit{pending}}\)
\(\)
\(\)
\(%\)
\(% Theory solver interface\)
\(%\)
\(\newcommand{\TSinit}[1]{\mathop{init}(#1)}\)
\(\newcommand{\TSassert}[1]{\mathop{assert}(#1)}\)
\(\newcommand{\TSretract}{\mathop{retract}()}\)
\(\newcommand{\TSisSat}{\mathop{isSat}()}\)
\(\newcommand{\TSgetModel}{\mathop{getModel}()}\)
\(\newcommand{\TSgetImplied}{\mathop{getImplied}()}\)
\(\newcommand{\TSexplain}[1]{\mathop{explain}(#1)}\)
\(\)
\(\)
\(\newcommand{\VarsOf}[1]{\mathop{vars}(#1)}\)
\(\)
\(\newcommand{\Dist}[1]{\mathit{dist}(#1)}\)
\(%\newcommand{\Dist}[1]{\mathit{dist}(#1)}\)
\(\)
\(%\)
\(% Nelson-Oppen\)
\(%\)
\(\newcommand{\TComb}{\cup}\)
\(\newcommand{\NOShared}[1]{\mathop{\textrm{shared}}(#1)}\)
\(\newcommand{\NOPart}{P}\)
\(\newcommand{\NOPartI}[1]{P_{#1}}\)
\(%\newcommand{\NOEq}{\mathrel{\approx}}\)
\(%\newcommand{\NOEqNot}{\mathrel{\not\approx}}\)
\(\newcommand{\NOEq}{\mathrel{{\equiv_{P}}}}\)
\(%\newcommand{\NOEq}{\stackrel{\NOPart}{\equiv}}\)
\(\newcommand{\NOEqNot}{\mathrel{\not\equiv_{\NOPart}}}\)
\(%\newcommand{\NOEqNot}{\stackrel{\NOPart}{\not\equiv}}\)
\(\newcommand{\NOArr}{\mathop{arr}(P)}\)
\(\newcommand{\NOArrI}[1]{\mathop{arr}(P_{#1})}\)
\(\)
\(%\)
\(% Example formulas in Nelson-Oppen part\)
\(%\)
\(\newcommand{\NOF}{\phi}\)
\(%\newcommand{\NOFA}{\phi_1}\)
\(%\newcommand{\NOFB}{\phi_2}\)
\(%\newcommand{\NOTA}{\ThI{1}}\)
\(%\newcommand{\NOTB}{\ThI{2}}\)
\(\newcommand{\NOFEUF}{\phi_\mathit{EUF}}\)
\(\newcommand{\NOFLIA}{\phi_\mathit{LIA}}\)
\(\newcommand{\NOFLRA}{\phi_\mathit{LRA}}\)
\(\newcommand{\NOFCons}{\phi_\textup{cons}}\)
\(\)
\(%\newcommand{\Asgn}{\mathrel{:=}}\)
\(\newcommand{\Asgn}{\mathrel{\leftarrow}}\)
\(\)
\(%\newcommand{\Engl}[1]{(engl.\ #1)}\)
\(\)
\(\newcommand{\Ack}[1]{\mathop{ack}(#1)}\)
\(\newcommand{\VVar}[1]{v_{#1}}\)
\(\newcommand{\FVar}[2]{{#1}_{#2}}\)
\(\newcommand{\PVar}[2]{{#1}_{#2}}\)
\(\newcommand{\Flat}{{\phi_\textrm{flat}}}\)
\(\newcommand{\Cong}{{\phi_\textrm{cong}}}\)
\(\)
\(\newcommand{\In}{\mathit{in}}\)
\(\newcommand{\Out}{\mathit{out}}\)
\(\)
\(\newcommand{\SubType}{\FuncName{subtype}}\)
\(\)
\(%\)
\(% Fourier-Motzkin elimination\)
\(%\)
\(\newcommand{\FM}{\phi}\)
\(\newcommand{\FMup}{\phi^\textrm{up}}\)
\(\newcommand{\FMlo}{\phi^\textrm{low}}\)
\(%\newcommand{\FMup}{\phi^{\le}}\)
\(%\newcommand{\FMlo}{\phi^{\ge}}\)
\(\newcommand{\FMindep}{\phi^{\ast}}\)
\(\newcommand{\Nup}{n^\textrm{up}}\)
\(\newcommand{\Nlo}{n^\textrm{low}}\)
\(%\newcommand{\Nup}{n^{\le}}\)
\(%\newcommand{\Nlo}{n^{\ge}}\)
\(\newcommand{\Rup}[1]{A^\textrm{up}_{#1}}\)
\(\newcommand{\Rlo}[1]{A^\textrm{low}_{#1}}\)
\(%\newcommand{\Rup}[1]{A^{\le}_{#1}}\)
\(%\newcommand{\Rlo}[1]{A^{\ge}_{#1}}\)
\(%\newcommand{\FMless}{\mathrel{\triangleleft}}\)
\(%\newcommand{\FMmore}{\mathrel{\triangleright}}\)
\(\)
\(\)
\(\)
\(\newcommand{\ProblemName}[1]{\textup{#1}}\)
\(\newcommand{\ATM}{A_\textup{TM}}\)
\(\newcommand{\PCP}{\ProblemName{PCP}}\)
\(\newcommand{\MPCP}{\ProblemName{MPCP}}\)
\(\newcommand{\PCPAst}{\star}\)
\(\)
\(\newcommand{\Eps}{\varepsilon}\)
\(\)
\(\newcommand{\List}[1]{[#1]}\)
\(\newcommand{\Strings}[1]{\{#1\}^\star}\)
\(\newcommand{\StringsOver}[1]{{#1}^\star}\)
\(\newcommand{\SigmaStrings}{\Sigma^\star}\)
\(\newcommand{\GammaStrings}{\Gamma^\star}\)
\(\newcommand{\Complement}[1]{\overline{#1}}\)
\(\)
\(\)
\(%\)
\(% SSA example\)
\(%\)
\(\newcommand{\In}{\mathit{in}}\)
\(\newcommand{\Out}{\mathit{out}}\)
\(\)
\(%\)
\(%\)
\(%\)
\(\newcommand{\DA}{♠}\)
\(\newcommand{\DB}{♥}\)
\(\newcommand{\DC}{♦}\)
\(\newcommand{\DD}{♣}\)
The Eager Approach
For some theories \( \Th \), it is possible to reduce
the problem of \( \Th \)-satisfiability of a quantifier-free formula \( \phi \)
into the problem of satisfiability of a propositional formula \( \psi \).
The workflow thus looks as follows:
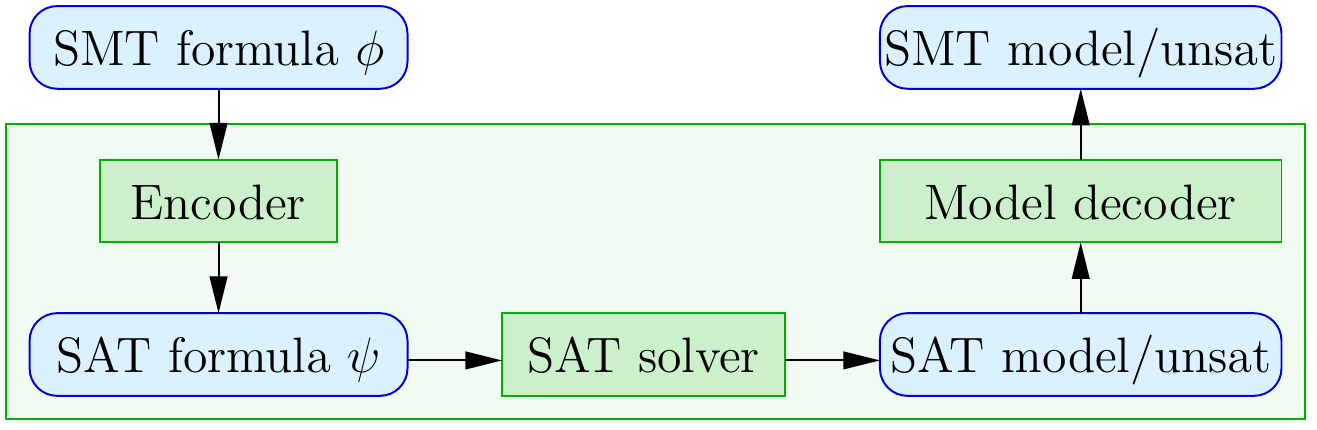
Therefore,
if the resulting SAT formula is of reasonable size,
one can leverage the highly efficient propositional SAT solvers
to solve \( \Th \)-satisfiability.
In the following, we sketch the idea for bit-vectors (without arrays/memories).
Recall that the theory of bit-vectors includes
the sort \( \BVS{n} \) for bit-vectors of width \( n \), and
the predicate and function symbols such as
constants for bit-vector values,
\( \BVLE{n} : \BVS{n} \times \BVS{n} \) for less-or-equal comparison,
\( \BVAdd{n} : \BVS{n} \times \BVS{n} \to \BVS{n} \) for addition (modulo \( 2^n \)), and
\( \BVSL{n} : \BVS{n} \times \BVS{n} \to \BVS{n} \) for shifting left (pad with zeros).
The domain of \( \BVS{n} \) is the set \( \Set{0,1}^n \) of all bit-vectors of length \( n \).
The predicate and function symbols interpreted as expected, e.g.,
\begin{eqnarray*}
1100 \BVLE4 1001 &=& \False\\\\
1100 \BVAdd4 1001 &=& 0101\\\\
00110001 \BVSL8 00000010 &=& 11000100
\end{eqnarray*}
Example
The formula
\( (x \BVGE{8} y) \land (x \BVAdd{8} 00000010 \BVLE{8} y) \)
is \( \BVT \)-satisfiable due to possibility of overflows
(e.g., \( x \mapsto 11111110 \) and \( y \mapsto 11110000 \)).
The eager approach for bit-vectors is called bit-blasting as
the bit-vectors are “blasted” into individual bits.
The procedure can be described as follows by using Boolean circuits:
For each bit-vector variable \( \Var \) of sort \( \BVS{n} \),
introduce \( n \) fresh input gates \( \BVVar{n-1},…,\BVVar{0} \).
In a bottom-up fashion,
encode each bit-vector predicate and function application
with a corresponding Boolean circuit so that
the circuit for a bit-vector term \( \Term \) of sort \( \BVS{n} \)
has the output gates \( \BVTermB{n-1},…,\BVTermB{0} \), and
the circuit for a bit-vector atom \( \Atom \)
has one output gate \( \BVAtom \).
The Boolean part of the formula is seen as a circuit as before.
The circuit can then be translated into CNF as usual.
Example
The circuit below shows an encoding for the atom \( (x \BVLE{3} y) \).
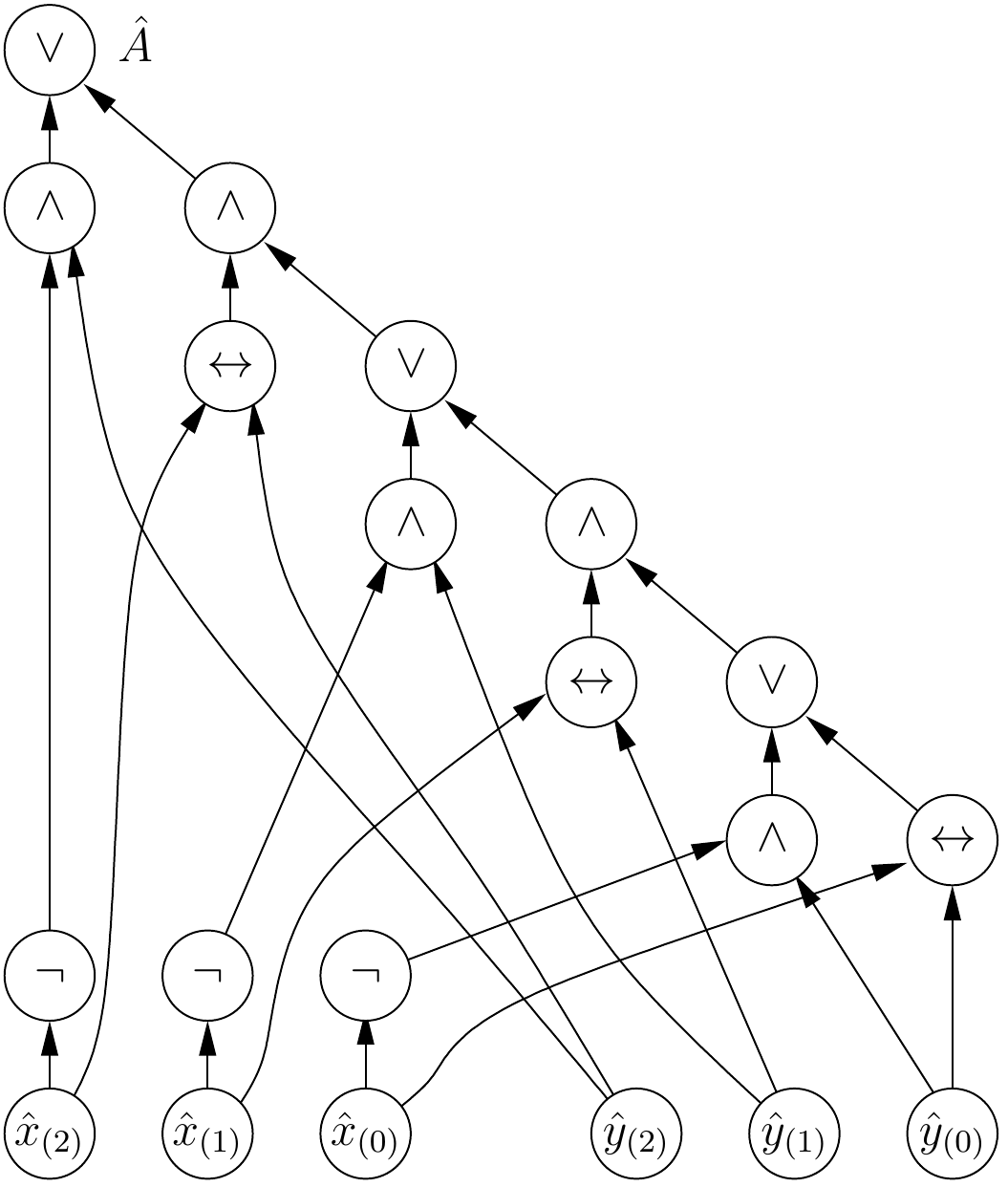
For encoding operations on bit-vectors one can use
any appropriate construction found in the hardware-design literature.
As an example, for addition one can use
a ripple-carry adder or some more complex carry lookahead adder,
see e.g. this wikipedia link.
Bit-blasting is conceptually simple and the basic version is also easy to implement in practise.
However, for some constructions such as multiplication and division,
the resulting cicuits and CNF formulas tend to get very large and difficult to solve.
Moreover, the higher level structure is lost and thus cannot be exploited by the SAT solver.
Therefore, state-of-the-art implementations do not use the basic approach as described above but
apply preprocessing (simplification) at the bit-vector level,
use incremental bit-blasting,
may use abstraction and refinement,
instantiate array axioms “on demand”,
and so on.
Some references:
R. Brummayer, A. Biere, and F. Lonsing:
BTOR: Bit-Precise Modelling of Word-Level Problems for Model Checking,
in Proc. BPR 2008, pp 33–38
D. Kroening and O. Strichman:
Decision Procedures — An Algorithmic Point of View, Chapter 6, Springer, 2008
S. Jha, R. Limaye, and S. Seshia:
Beaver: Engineering an Efficient SMT Solver for Bit-Vector Arithmetic,
in Proc. CAV 2009, pp 668–674
R. Bryant, D. Kroening, J. Ouaknine, S. Seshia, O. Strichman, and B. Brady:
An abstraction-based decision procedure for bit-vector arithmetic,
Int. J. Softw. Tools Technol. Transf. 11(2):95–104, 2009
Combining with arrays:
Complexity:

