Note
Go to the end to download the full example code.
Compute RSA between RDMs#
This example showcases the most basic version of RSA: computing the similarity between two RDMs. Then we continue with computing RSA between many RDMs efficiently.
# sphinx_gallery_thumbnail_number=2
import mne
import mne_rsa
# Import required packages
import pandas as pd
from matplotlib import pyplot as plt
MNE-Python contains a build-in data loader for the kiloword dataset, which is used
here as an example dataset. Since we only need the words shown during the experiment,
which are in the metadata, we can pass preload=False to prevent MNE-Python from
loading the EEG data, which is a nice speed gain.
data_path = mne.datasets.kiloword.data_path(verbose=True)
epochs = mne.read_epochs(data_path / "kword_metadata-epo.fif")
# Show the metadata of 10 random epochs
epochs.metadata.sample(10)
Compute RDMs based on word length and visual complexity.
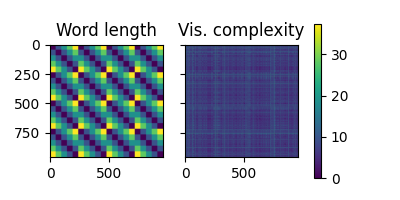
<Figure size 400x200 with 3 Axes>
Perform RSA between the two RDMs using Spearman correlation
rsa_result = mne_rsa.rsa(rdm1, rdm2, metric="spearman")
print("RSA score:", rsa_result)
RSA score: 0.026439883289118758
We can compute RSA between multiple RDMs by passing lists to the mne_rsa.rsa()
function.
# Create RDMs for each stimulus property
columns = metadata.columns[1:] # Skip the first column: WORD
rdms = [mne_rsa.compute_rdm(metadata[col], metric="euclidean") for col in columns]
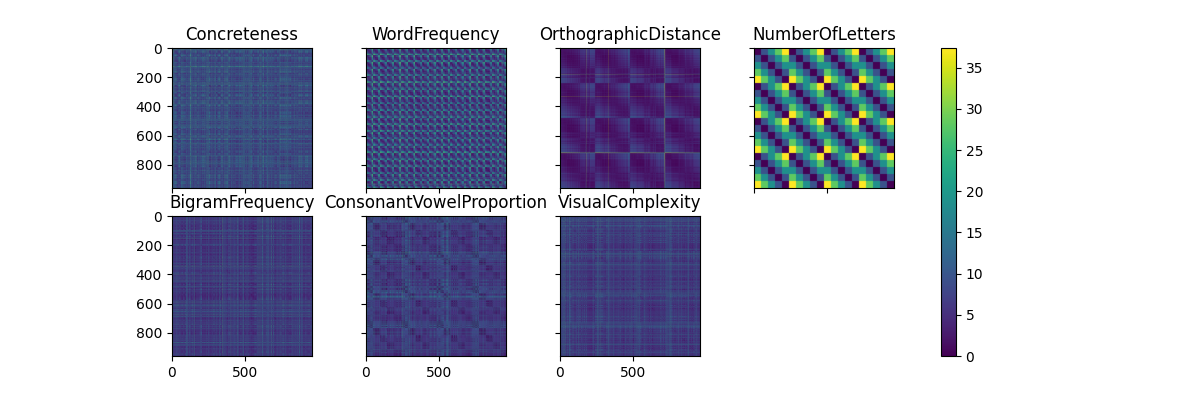
# Plot the RDMs
fig = mne_rsa.plot_rdms(rdms, names=columns, n_rows=2)
fig.set_size_inches(12, 4)
# Compute RSA between the first two RDMs (Concreteness and WordFrequency) and the
# others.
rsa_results = mne_rsa.rsa(rdms[:2], rdms[2:], metric="spearman")
# Pack the result into a Pandas DataFrame for easy viewing
print(pd.DataFrame(rsa_results, index=columns[:2], columns=columns[2:]))
OrthographicDistance NumberOfLetters BigramFrequency ConsonantVowelProportion VisualComplexity
Concreteness 0.031064 0.026832 -0.004681 0.005647 0.004263
WordFrequency 0.058385 0.013607 0.001970 -0.003850 -0.009620
What if we have many RDMs? The mne_rsa.rsa() function is optimized for the case
where the first parameter (the “data” RDMs) is a large list of RDMs and the second
parameter (the “model” RDMs) is a smaller list. To save memory, you can also pass
generators instead of lists.
Let’s create a generator that creates RDMs for each time-point in the EEG data and
compute the RSA between those RDMs and all the “model” RDMs we computed above. This is
a basic example of using a “searchlight” and in other examples, you can learn how to
use the searchlight generator to build more advanced searchlights. However,
since this is such a simple case, it is educational to construct the generator
manually.
The RSA computation will take some time. Therefore, we pass a few extra parameters to
mne_rsa.rsa() to enable some improvements. First, the verbose=True enables a
progress bar. However, since we are using a generator, the progress bar cannot
automatically infer how many RDMs there will be. Hence, we provide this information
explicitly using the n_data_rdms parameter. Finally, depending on how many CPUs
you have on your system, consider increasing the n_jobs parameter to parallelize
the computation over multiple CPUs.
epochs.resample(100) # Downsample to speed things up for this example
eeg_data = epochs.get_data()
n_trials, n_sensors, n_times = eeg_data.shape
def generate_eeg_rdms():
"""Generate RDMs for each time sample."""
for i in range(n_times):
yield mne_rsa.compute_rdm(eeg_data[:, :, i], metric="correlation")
rsa_results = mne_rsa.rsa(
generate_eeg_rdms(),
rdms,
metric="spearman",
verbose=True,
n_data_rdms=n_times,
n_jobs=1,
)
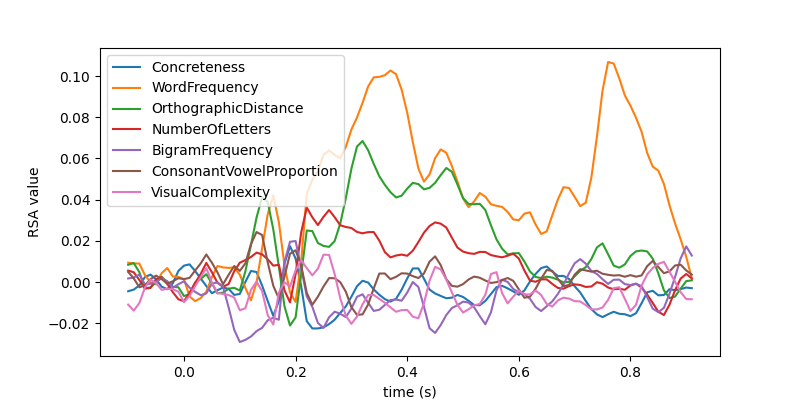
# Plot the RSA values over time using standard matplotlib commands
plt.figure(figsize=(8, 4))
plt.plot(epochs.times, rsa_results)
plt.xlabel("time (s)")
plt.ylabel("RSA value")
plt.legend(columns)
0%| | 0/102 [00:00<?, ?RDM/s]
1%|█▋ | 1/102 [00:00<01:16, 1.32RDM/s]
2%|███▎ | 2/102 [00:00<00:40, 2.44RDM/s]
3%|█████ | 3/102 [00:01<00:30, 3.23RDM/s]
4%|██████▋ | 4/102 [00:01<00:29, 3.35RDM/s]
5%|████████▍ | 5/102 [00:01<00:24, 3.97RDM/s]
6%|██████████ | 6/102 [00:01<00:21, 4.48RDM/s]
7%|███████████▋ | 7/102 [00:01<00:19, 4.86RDM/s]
8%|█████████████▍ | 8/102 [00:02<00:19, 4.92RDM/s]
9%|███████████████ | 9/102 [00:02<00:18, 5.13RDM/s]
10%|████████████████▋ | 10/102 [00:02<00:17, 5.35RDM/s]
11%|██████████████████▎ | 11/102 [00:02<00:16, 5.42RDM/s]
12%|████████████████████ | 12/102 [00:02<00:16, 5.40RDM/s]
13%|█████████████████████▋ | 13/102 [00:02<00:16, 5.48RDM/s]
14%|███████████████████████▎ | 14/102 [00:03<00:16, 5.47RDM/s]
15%|█████████████████████████ | 15/102 [00:03<00:16, 5.41RDM/s]
16%|██████████████████████████▋ | 16/102 [00:03<00:15, 5.42RDM/s]
17%|████████████████████████████▎ | 17/102 [00:03<00:15, 5.38RDM/s]
18%|██████████████████████████████ | 18/102 [00:03<00:15, 5.37RDM/s]
19%|███████████████████████████████▋ | 19/102 [00:04<00:14, 5.59RDM/s]
20%|█████████████████████████████████▎ | 20/102 [00:04<00:13, 6.10RDM/s]
21%|███████████████████████████████████ | 21/102 [00:04<00:11, 6.84RDM/s]
23%|██████████████████████████████████████▎ | 23/102 [00:04<00:09, 8.15RDM/s]
24%|████████████████████████████████████████ | 24/102 [00:04<00:09, 8.36RDM/s]
25%|█████████████████████████████████████████▋ | 25/102 [00:04<00:08, 8.71RDM/s]
26%|█████████████████████████████████████████████ | 27/102 [00:04<00:08, 9.31RDM/s]
28%|████████████████████████████████████████████████▎ | 29/102 [00:05<00:07, 9.88RDM/s]
30%|███████████████████████████████████████████████████▋ | 31/102 [00:05<00:06, 10.27RDM/s]
32%|███████████████████████████████████████████████████████ | 33/102 [00:05<00:06, 10.48RDM/s]
34%|██████████████████████████████████████████████████████████▎ | 35/102 [00:05<00:06, 10.65RDM/s]
36%|█████████████████████████████████████████████████████████████▋ | 37/102 [00:05<00:06, 10.51RDM/s]
38%|█████████████████████████████████████████████████████████████████ | 39/102 [00:06<00:06, 10.46RDM/s]
40%|████████████████████████████████████████████████████████████████████▎ | 41/102 [00:06<00:05, 10.36RDM/s]
42%|███████████████████████████████████████████████████████████████████████▋ | 43/102 [00:06<00:05, 10.24RDM/s]
44%|███████████████████████████████████████████████████████████████████████████ | 45/102 [00:06<00:05, 10.31RDM/s]
46%|██████████████████████████████████████████████████████████████████████████████▎ | 47/102 [00:06<00:05, 10.37RDM/s]
48%|█████████████████████████████████████████████████████████████████████████████████▋ | 49/102 [00:06<00:05, 10.43RDM/s]
50%|█████████████████████████████████████████████████████████████████████████████████████ | 51/102 [00:07<00:04, 10.44RDM/s]
52%|████████████████████████████████████████████████████████████████████████████████████████▎ | 53/102 [00:07<00:05, 9.77RDM/s]
54%|███████████████████████████████████████████████████████████████████████████████████████████▋ | 55/102 [00:07<00:04, 9.99RDM/s]
56%|███████████████████████████████████████████████████████████████████████████████████████████████ | 57/102 [00:07<00:04, 10.15RDM/s]
58%|██████████████████████████████████████████████████████████████████████████████████████████████████▎ | 59/102 [00:07<00:04, 10.39RDM/s]
60%|█████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 61/102 [00:08<00:03, 10.55RDM/s]
62%|█████████████████████████████████████████████████████████████████████████████████████████████████████████ | 63/102 [00:08<00:03, 10.63RDM/s]
64%|████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 65/102 [00:08<00:03, 10.73RDM/s]
66%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 67/102 [00:08<00:03, 10.70RDM/s]
68%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 69/102 [00:08<00:03, 10.82RDM/s]
70%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 71/102 [00:09<00:02, 10.72RDM/s]
72%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 73/102 [00:09<00:02, 10.61RDM/s]
74%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 75/102 [00:09<00:02, 10.68RDM/s]
75%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 77/102 [00:09<00:02, 10.04RDM/s]
77%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 79/102 [00:09<00:02, 9.91RDM/s]
79%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 81/102 [00:10<00:02, 10.13RDM/s]
81%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 83/102 [00:10<00:01, 10.26RDM/s]
83%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 85/102 [00:10<00:01, 10.39RDM/s]
85%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 87/102 [00:10<00:01, 10.46RDM/s]
87%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 89/102 [00:10<00:01, 10.49RDM/s]
89%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 91/102 [00:11<00:01, 10.54RDM/s]
91%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 93/102 [00:11<00:00, 10.56RDM/s]
93%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 95/102 [00:11<00:00, 10.52RDM/s]
95%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 97/102 [00:11<00:00, 10.41RDM/s]
97%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 99/102 [00:11<00:00, 10.42RDM/s]
99%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 101/102 [00:12<00:00, 9.95RDM/s]
100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 102/102 [00:12<00:00, 8.42RDM/s]
<matplotlib.legend.Legend object at 0x00000233824A04A0>
Total running time of the script: (0 minutes 19.371 seconds)