Graphs, isomorphism, and canonical labeling¶
Below we briefly describe what bliss does. For the algorithms and data structures of bliss, please refer to the papers mentioned at the main page.
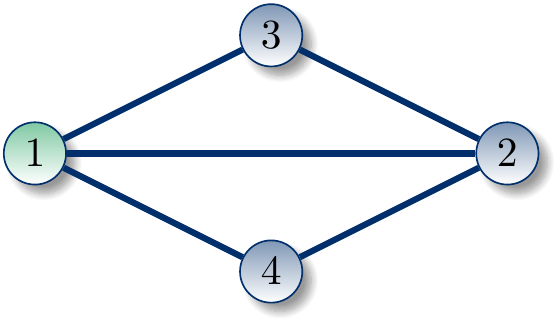
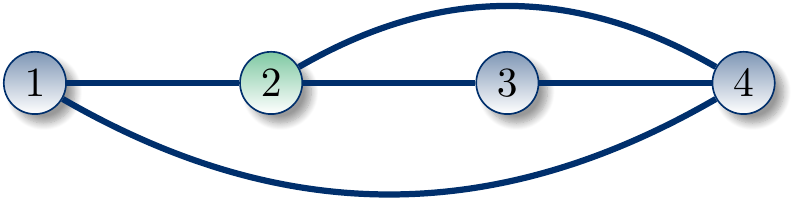
Mathematically, a colored graph is a triple \(G=(V,E,c)\), where \(V=\{1,2,...,n\}\) is a finite set of vertices, \(E\) is a set of 2-element subsets of \(V\) called edges, and \(c: V \to \mathbb{N}\) is a function that associates to each vertex an integer “color”. For example, identifying blue with 0 and green with 1, the graphs in the figure below are formally
and
\(G_1\)¶ |
\(G_2\)¶ |
Let \(\gamma: V \to V\) be a permutation of \(V\). Denote by \(v^\gamma\) the image of \(v \in V\) under \(\gamma\). For a colored graph \(G=(V,E,c)\), define the colored graph
where \(c^\gamma: V \to \mathbb{N}\) is defined by \(c^\gamma(v^\gamma) = c(v)\) for all \(v \in V\).
Two colored graphs, \(G\) and \(H\), are isomorphic if there exists a permutation \(\gamma: V \to V\) such that \(G^\gamma = H\). Such a permutation \(\gamma\) is called an isomorphism of \(G\) onto \(H\). For example, there are two possible isomorphisms of \(G_1\) onto \(G_2\) shown in the figure above, namely \(\{1 \to 2,2 \to 4,3 \to 1,4 \to 3\}\) and \(\{1 \to 2,2 \to 4,3 \to 3,4 \to 1\}\). We write \(G \cong H\) to denote that the graphs \(G\) and \(H\) are isomorphic.
An automorphism of a colored graph is an isomorphism of the colored graph onto itself. The set of all automorphisms of a colored graph \(G\) forms a permutation group, where the group operation is the functional composition of permutations. This permutation group is called the automorphism group of \(G\), and is denoted by \(\mathrm{Aut}(G)\). A set of generators for \(\mathrm{Aut}(G)\) is a set \(S \subseteq \mathrm{Aut}(G)\) such that every non-identity permutation in \(\mathrm{Aut}(G)\) can be obtained by composing some elements of \(S\). For example, \(\{1 \to 1,2 \to 2,3 \to 4,4\to 3\}\) is a set of generators for the automorphism group
of the graph \(G_1\) shown in the figure above.
A function \(\rho\) from colored graphs to colored graphs is a canonical labeling map if the following two conditions hold:
The canonical form \(\rho(G)\) of a graph \(G\) is isomorphic to the graph: for all colored graphs \(G\) it holds that \(ρ(G) \cong G\).
The canonical forms of two graphs are the same if, and only if, the graphs are isomorphic: for all colored graphs \(G\) and \(H\) it holds that \(G \cong H\) if and only if \(ρ(G)=ρ(H)\).
A canonical labeling of \(G\) (under \(\rho\)) is an isomorphism of \(G\) onto its canonical form \(ρ(G)\). Given a colored graph \(G\) as input, the software tool bliss computes the canonical form \(ρ(G)\) and an associated canonical labeling. Also computed is a set of generators for \(\mathrm{Aut}(G)\).
A note on canonical forms¶
In general, the computed canonical form depends on the version and applied options of bliss. Therefore, if you are building and storing a library of graphs in canonical form — for example, to classify some combinatorial structures up to isomorphism — be sure to use the same version of bliss with the same options all the time. In principle, the canonical forms should not depend on the computer platform in which bliss is compiled and run, but this has not been extensively tested in practice.
Directed Graphs¶
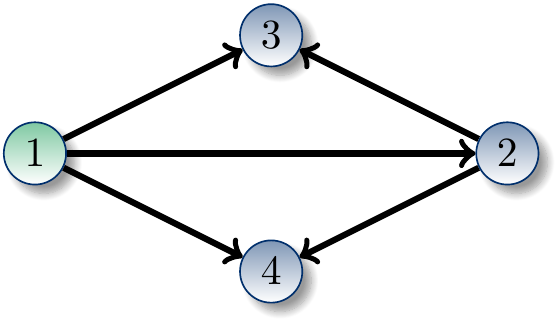
The software tool bliss can also handle directed graphs (also called “digraphs”). Formally, a directed colored graph is a triple \(G=(V,E,c)\), where \(V\) and \(c\) are the vertex set and the color function as in the undirected case above, but \(E \subseteq V \times V\) is now a set directed edges. As an example, identifying blue with 0 and green with 1, the directed graph
is
Given a permutation \(\gamma: V \to V\) and a directed colored graph \(G=(V,E,c)\), define the directed colored graph
The definitions of automorhism, isomorphism, generating sets, and canonical labelings for directed colored graphs are the same as for undirected colored graphs.