Automatic post-hoc optimization of linear models¶

This example will demonstrate how to define custom modifications to a linear model that introduce new hyperparameters. We will then use post-hoc’s optimizer to find the optimal values for these hyperparameters.

We will start with ordinary linear regression as a base model. Then, we will modify the covariance matrix by applying shrinkage, modify the pattern with a Gaussian kernel and modify the normalizer to be “unit noise gain”, meaning the weights all sum to 1.

Author: Marijn van Vliet <w.m.vanvliet@gmail.com>

# Required imports
from matplotlib import pyplot as plt
from posthoc import Workbench, WorkbenchOptimizer, cov_estimators, normalizers
from scipy.stats import norm, pearsonr
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_predict
from sklearn.preprocessing import normalize
from functools import partial
import mne
import numpy as np

We will use some data from the original publication 1. A participant was silently reading word-pairs. In these pairs, the two words had a varying forward association strength between them. For example: locomotiv -> train has a high association strength, and dog -> submarine has not. In the case of word-pairs with high association strength, the brain will process second word is faster, since it has been semantically primed by the first word.

We are going to deduce the memory priming effect from epochs of EEG data and use that to predict what the forward association strength was for a given word-pair.

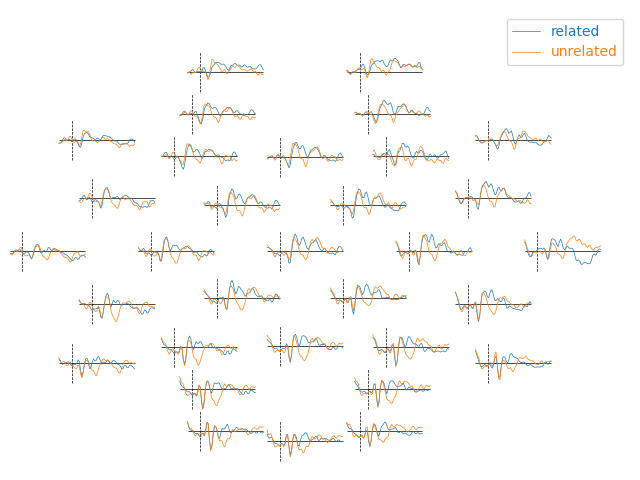
Let’s first load the data and plot a contrast between word-pairs with a high versus low association strength, so we can observe how the memory priming effect manifests in the EEG data.

epochs = mne.read_epochs('subject04-epo.fif')
related = epochs['FAS > 0.2'].average()
related.comment = 'related'
unrelated = epochs['FAS < 0.2'].average()
unrelated.comment = 'unrelated'
mne.viz.plot_evoked_topo([related, unrelated])

Out:

<Figure size 640x480 with 1 Axes>

Around 400ms after the presentation of the second word, there is a negative peak named the N400 potential. We can clearly observe the semantic priming effect as the N400 is more prominent in cases where the words have a low forward associative strength.

A naive approach to deduce the forward association strength from a word pair is to take the average signal around 400ms at some sensors that show the N400 well:

ROI = epochs.copy()
ROI.pick_channels(['P3', 'Pz', 'P4'])
ROI.crop(0.3, 0.47)
FAS_pred = ROI.get_data().mean(axis=(1, 2))

perf_naive, _ = pearsonr(epochs.metadata['FAS'], FAS_pred)
print(f'Performance: {perf_naive:.2f}')

Out:

Performance: 0.30

Let’s try ordinary linear regression next, using 10-fold cross-validation.

X = normalize(epochs.get_data().reshape(200, 32 * 60))
y = epochs.metadata['FAS'].values
ols = LinearRegression()
FAS_pred = cross_val_predict(ols, X, y, cv=10)
perf_ols, _ = pearsonr(epochs.metadata['FAS'], FAS_pred)
print(f'Performance: {perf_ols:.2f} (to beat: {perf_naive:.2f})')

Out:

Performance: 0.21 (to beat: 0.30)

Feeding all data into a linear regression model performs worse than taking the average signal in a well chosen sensors. That is because the model is overfitting. We could restrict the data going into the model to the same sensors and time window as we did when averaging the signal, but we can do so much better.

Let’s use the post-hoc framework to modify the linear regression model and incorporate some information about the nature of the data and the N400 potential.

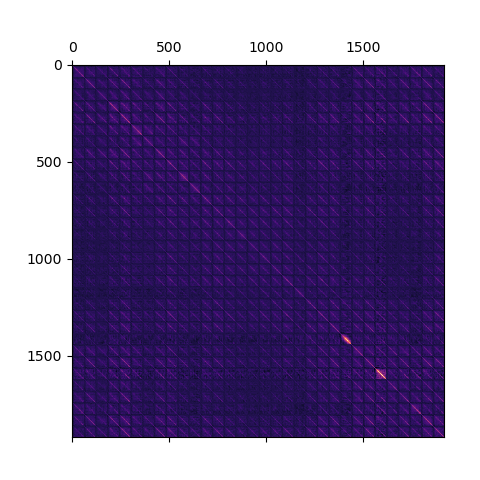
First, let’s try to reduce overfitting by applying some shrinkage to the covariance matrix. The data consists of 32 EEG electrodes, each recording 60 samples of data. This causes a clear pattern to appear in the covariance matrix:

plt.figure()
plt.matshow(np.cov(X.T), cmap='magma')

Out:

<matplotlib.image.AxesImage object at 0x000002BC96F5DA00>

The covariance matrix is build up from 32x32 squares, each square being 60x60. The KroneckerShrinkage class can make use of this information and apply different amounts of shrinkage to the diagonal of each square and the covariance matrix overall.

cov = cov_estimators.KroneckerKernel(outer_size=32, inner_size=60)

To use the Kronecker shrinkage determine the optimal amount of shrinkage to apply, we can wrap our linear regression model in the WorkbenchOptimizer class. By default, this uses heavily optimized leave-one-out cross-validation with a gradient descent algorithm to find the best values.

# We're optimizing for correlation between model prediction and true FAS
def scorer(model, X, y):
    return pearsonr(model.predict(X), y)[0]

# Construct the post-hoc workbench, tell it to modify the model by applying
# Kronecker shrinkage.
model = WorkbenchOptimizer(ols, cov=cov, scoring=scorer).fit(X, y)

shrinkage_params = model.cov_params_
print('Optimal shrinkage parameters:', shrinkage_params)

Out:

Computing patterns for each leave-one-out iteration...
Fit intercept: yes
Normalize: no
Choosing optimized code-path for LinearRegression() model.
Using kernel path.
cov_params=(0.5, 0.5), pattern_modifier_params=(), normalizer_modifier_params=() score=0.128617
cov_params=(0.5, 0.5), pattern_modifier_params=(), normalizer_modifier_params=() score=0.128617
cov_params=(0.501, 0.5), pattern_modifier_params=(), normalizer_modifier_params=() score=0.128665
cov_params=(0.5, 0.501), pattern_modifier_params=(), normalizer_modifier_params=() score=0.128489
cov_params=(0.5475143042386605, 0.37168759154748676), pattern_modifier_params=(), normalizer_modifier_params=() score=0.151458
cov_params=(0.5485143042386605, 0.37168759154748676), pattern_modifier_params=(), normalizer_modifier_params=() score=0.151526
cov_params=(0.5475143042386605, 0.37268759154748676), pattern_modifier_params=(), normalizer_modifier_params=() score=0.151266
cov_params=(0.6152884717698088, 0.1794167207357365), pattern_modifier_params=(), normalizer_modifier_params=() score=0.213952
cov_params=(0.6162884717698088, 0.1794167207357365), pattern_modifier_params=(), normalizer_modifier_params=() score=0.214079
cov_params=(0.6152884717698088, 0.1804167207357365), pattern_modifier_params=(), normalizer_modifier_params=() score=0.213513
cov_params=(0.6785316392745661, 0.0), pattern_modifier_params=(), normalizer_modifier_params=() score=0.303706
cov_params=(0.6795316392745661, 0.0), pattern_modifier_params=(), normalizer_modifier_params=() score=0.303890
cov_params=(0.6785316392745661, 0.001), pattern_modifier_params=(), normalizer_modifier_params=() score=0.312336
cov_params=(0.61866807939433, 0.1698289954321378), pattern_modifier_params=(), normalizer_modifier_params=() score=0.218710
cov_params=(0.61966807939433, 0.1698289954321378), pattern_modifier_params=(), normalizer_modifier_params=() score=0.218841
cov_params=(0.61866807939433, 0.1708289954321378), pattern_modifier_params=(), normalizer_modifier_params=() score=0.218249
cov_params=(0.6601594401656801, 0.05212072460748246), pattern_modifier_params=(), normalizer_modifier_params=() score=0.300725
cov_params=(0.6611594401656801, 0.05212072460748246), pattern_modifier_params=(), normalizer_modifier_params=() score=0.300878
cov_params=(0.6601594401656801, 0.05312072460748246), pattern_modifier_params=(), normalizer_modifier_params=() score=0.299882
cov_params=(0.6721658286859352, 0.018059387372573676), pattern_modifier_params=(), normalizer_modifier_params=() score=0.329133
cov_params=(0.6731658286859352, 0.018059387372573676), pattern_modifier_params=(), normalizer_modifier_params=() score=0.329258
cov_params=(0.6721658286859352, 0.019059387372573677), pattern_modifier_params=(), normalizer_modifier_params=() score=0.328614
cov_params=(0.7971864936933489, 0.0), pattern_modifier_params=(), normalizer_modifier_params=() score=0.327041
cov_params=(0.7981864936933489, 0.0), pattern_modifier_params=(), normalizer_modifier_params=() score=0.327251
cov_params=(0.7971864936933489, 0.001), pattern_modifier_params=(), normalizer_modifier_params=() score=0.331873
cov_params=(0.7362515282264148, 0.008802129998560695), pattern_modifier_params=(), normalizer_modifier_params=() score=0.337934
cov_params=(0.7372515282264148, 0.008802129998560695), pattern_modifier_params=(), normalizer_modifier_params=() score=0.338059
cov_params=(0.7362515282264148, 0.009802129998560696), pattern_modifier_params=(), normalizer_modifier_params=() score=0.338368
cov_params=(0.8249149452241371, 0.0045867872725880885), pattern_modifier_params=(), normalizer_modifier_params=() score=0.345517
cov_params=(0.8259149452241371, 0.0045867872725880885), pattern_modifier_params=(), normalizer_modifier_params=() score=0.345663
cov_params=(0.8249149452241371, 0.0055867872725880886), pattern_modifier_params=(), normalizer_modifier_params=() score=0.346892
cov_params=(1.0, 0.0), pattern_modifier_params=(), normalizer_modifier_params=() score=0.297086
cov_params=(0.999, 0.0), pattern_modifier_params=(), normalizer_modifier_params=() score=0.312730
cov_params=(1.0, 0.001), pattern_modifier_params=(), normalizer_modifier_params=() score=0.297086
cov_params=(0.8945405407430417, 0.002762772105894922), pattern_modifier_params=(), normalizer_modifier_params=() score=0.353331
cov_params=(0.8955405407430417, 0.002762772105894922), pattern_modifier_params=(), normalizer_modifier_params=() score=0.353489
cov_params=(0.8945405407430417, 0.003762772105894922), pattern_modifier_params=(), normalizer_modifier_params=() score=0.354723
cov_params=(0.962123177308625, 0.0009922773161266168), pattern_modifier_params=(), normalizer_modifier_params=() score=0.359635
cov_params=(0.963123177308625, 0.0009922773161266168), pattern_modifier_params=(), normalizer_modifier_params=() score=0.359641
cov_params=(0.962123177308625, 0.001992277316126617), pattern_modifier_params=(), normalizer_modifier_params=() score=0.360245
cov_params=(0.9423239917892359, 0.002780662328775404), pattern_modifier_params=(), normalizer_modifier_params=() score=0.359813
cov_params=(0.9433239917892359, 0.002780662328775404), pattern_modifier_params=(), normalizer_modifier_params=() score=0.359902
cov_params=(0.9423239917892359, 0.003780662328775404), pattern_modifier_params=(), normalizer_modifier_params=() score=0.360618
cov_params=(0.9352708588718786, 0.007470138094729195), pattern_modifier_params=(), normalizer_modifier_params=() score=0.362489
cov_params=(0.9362708588718786, 0.007470138094729195), pattern_modifier_params=(), normalizer_modifier_params=() score=0.362556
cov_params=(0.9352708588718786, 0.008470138094729195), pattern_modifier_params=(), normalizer_modifier_params=() score=0.362981
cov_params=(0.9348100949822981, 0.013358888211589011), pattern_modifier_params=(), normalizer_modifier_params=() score=0.364529
cov_params=(0.9358100949822981, 0.013358888211589011), pattern_modifier_params=(), normalizer_modifier_params=() score=0.364588
cov_params=(0.9348100949822981, 0.01435888821158901), pattern_modifier_params=(), normalizer_modifier_params=() score=0.364712
cov_params=(0.9516666877061215, 0.016280071434003486), pattern_modifier_params=(), normalizer_modifier_params=() score=0.365456
cov_params=(0.9526666877061215, 0.016280071434003486), pattern_modifier_params=(), normalizer_modifier_params=() score=0.365438
cov_params=(0.9516666877061215, 0.017280071434003487), pattern_modifier_params=(), normalizer_modifier_params=() score=0.365567
cov_params=(0.9489996860582463, 0.0193851650562842), pattern_modifier_params=(), normalizer_modifier_params=() score=0.365721
cov_params=(0.9499996860582463, 0.0193851650562842), pattern_modifier_params=(), normalizer_modifier_params=() score=0.365726
cov_params=(0.9489996860582463, 0.0203851650562842), pattern_modifier_params=(), normalizer_modifier_params=() score=0.365753
Optimal shrinkage parameters: [0.9489996860582463, 0.0193851650562842]

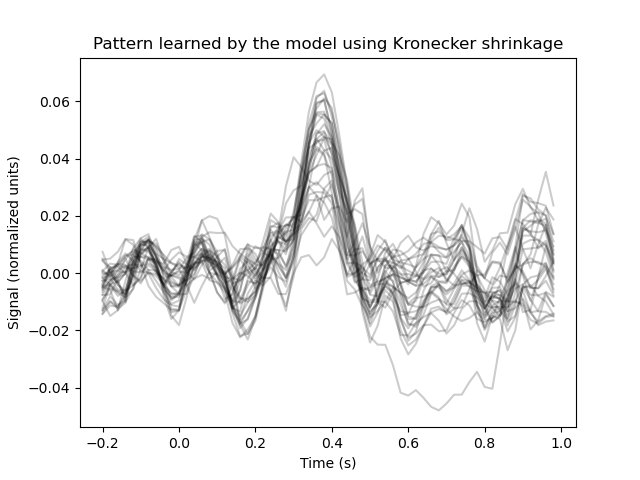
Let’s inspect the pattern that the model has learned:

plt.figure()
plt.plot(epochs.times, model.pattern_.reshape(32, 60).T, color='black', alpha=0.2)
plt.xlabel('Time (s)')
plt.ylabel('Signal (normalized units)')
plt.title('Pattern learned by the model using Kronecker shrinkage')

Pattern learned by the model using Kronecker shrinkage

Out:

Text(0.5, 1.0, 'Pattern learned by the model using Kronecker shrinkage')

We can clearly see that the model is picking up on the N400. Let’s fine-tune the pattern a bit by multiplying it with a Guassian kernel, centered around 400 ms.

def pattern_modifier(pattern, X, y, mean, std):
    """Multiply the pattern with a Gaussian kernel."""
    n_channels, n_samples = 32, 60
    kernel = norm(mean, std).pdf(np.arange(n_samples))
    kernel /= kernel.max()
    mod_pattern = pattern.reshape(n_channels, n_samples)
    mod_pattern = mod_pattern * kernel[np.newaxis, :]
    return mod_pattern.reshape(pattern.shape)

Now the optimizer has four hyperparameters to tune: two shrinkage values and two values dictating the shape of the Gaussian kernel.

model_opt = WorkbenchOptimizer(
    ols,
    cov=cov,
    pattern_modifier=pattern_modifier,
    pattern_param_x0=[30, 5],  # Initial guess for decent kernel shape
    pattern_param_bounds=[(0, 60), (2, None)],  # Boundaries for what values to try
    normalizer_modifier=normalizers.unit_gain,
    scoring=scorer,
).fit(X, y)

Out:

Computing patterns for each leave-one-out iteration...
Fit intercept: yes
Normalize: no
Choosing optimized code-path for LinearRegression() model.
Using kernel path.
cov_params=(0.5, 0.5), pattern_modifier_params=(30.0, 5.0), normalizer_modifier_params=() score=0.238878
cov_params=(0.5, 0.5), pattern_modifier_params=(30.0, 5.0), normalizer_modifier_params=() score=0.238878
cov_params=(0.501, 0.5), pattern_modifier_params=(30.0, 5.0), normalizer_modifier_params=() score=0.238909
cov_params=(0.5, 0.501), pattern_modifier_params=(30.0, 5.0), normalizer_modifier_params=() score=0.238779
cov_params=(0.5, 0.5), pattern_modifier_params=(30.001, 5.0), normalizer_modifier_params=() score=0.238870
cov_params=(0.5, 0.5), pattern_modifier_params=(30.0, 5.001), normalizer_modifier_params=() score=0.238855
cov_params=(0.5310971479546562, 0.4016941829457773), pattern_modifier_params=(29.99198616260383, 4.977396261185516), normalizer_modifier_params=() score=0.251690
cov_params=(0.5320971479546562, 0.4016941829457773), pattern_modifier_params=(29.99198616260383, 4.977396261185516), normalizer_modifier_params=() score=0.251735
cov_params=(0.5310971479546562, 0.4026941829457773), pattern_modifier_params=(29.99198616260383, 4.977396261185516), normalizer_modifier_params=() score=0.251561
cov_params=(0.5310971479546562, 0.4016941829457773), pattern_modifier_params=(29.99298616260383, 4.977396261185516), normalizer_modifier_params=() score=0.251682
cov_params=(0.5310971479546562, 0.4016941829457773), pattern_modifier_params=(29.99198616260383, 4.978396261185516), normalizer_modifier_params=() score=0.251667
cov_params=(0.5765024048484941, 0.27285167506202446), pattern_modifier_params=(29.98404622431943, 4.955346354637884), normalizer_modifier_params=() score=0.275617
cov_params=(0.5775024048484941, 0.27285167506202446), pattern_modifier_params=(29.98404622431943, 4.955346354637884), normalizer_modifier_params=() score=0.275692
cov_params=(0.5765024048484941, 0.27385167506202446), pattern_modifier_params=(29.98404622431943, 4.955346354637884), normalizer_modifier_params=() score=0.275416
cov_params=(0.5765024048484941, 0.27285167506202446), pattern_modifier_params=(29.985046224319433, 4.955346354637884), normalizer_modifier_params=() score=0.275609
cov_params=(0.5765024048484941, 0.27285167506202446), pattern_modifier_params=(29.98404622431943, 4.956346354637884), normalizer_modifier_params=() score=0.275596
cov_params=(0.6726577855810936, 0.0), pattern_modifier_params=(29.9672317001661, 4.908650943043517), normalizer_modifier_params=() score=0.343913
cov_params=(0.6736577855810936, 0.0), pattern_modifier_params=(29.9672317001661, 4.908650943043517), normalizer_modifier_params=() score=0.344053
cov_params=(0.6726577855810936, 0.001), pattern_modifier_params=(29.9672317001661, 4.908650943043517), normalizer_modifier_params=() score=0.348688
cov_params=(0.6726577855810936, 0.0), pattern_modifier_params=(29.9682317001661, 4.908650943043517), normalizer_modifier_params=() score=0.343906
cov_params=(0.6726577855810936, 0.0), pattern_modifier_params=(29.9672317001661, 4.909650943043517), normalizer_modifier_params=() score=0.343914
cov_params=(0.5809782829125139, 0.26015086915978014), pattern_modifier_params=(29.983263535308776, 4.953172758455817), normalizer_modifier_params=() score=0.278623
cov_params=(0.5819782829125139, 0.26015086915978014), pattern_modifier_params=(29.983263535308776, 4.953172758455817), normalizer_modifier_params=() score=0.278701
cov_params=(0.5809782829125139, 0.26115086915978014), pattern_modifier_params=(29.983263535308776, 4.953172758455817), normalizer_modifier_params=() score=0.278412
cov_params=(0.5809782829125139, 0.26015086915978014), pattern_modifier_params=(29.984263535308777, 4.953172758455817), normalizer_modifier_params=() score=0.278616
cov_params=(0.5809782829125139, 0.26015086915978014), pattern_modifier_params=(29.983263535308776, 4.954172758455817), normalizer_modifier_params=() score=0.278603
cov_params=(0.6443532335067832, 0.08031734039754651), pattern_modifier_params=(29.97218126794771, 4.922396327847094), normalizer_modifier_params=() score=0.343618
cov_params=(0.6453532335067832, 0.08031734039754651), pattern_modifier_params=(29.97218126794771, 4.922396327847094), normalizer_modifier_params=() score=0.343742
cov_params=(0.6443532335067832, 0.08131734039754651), pattern_modifier_params=(29.97218126794771, 4.922396327847094), normalizer_modifier_params=() score=0.343154
cov_params=(0.6443532335067832, 0.08031734039754651), pattern_modifier_params=(29.973181267947712, 4.922396327847094), normalizer_modifier_params=() score=0.343614
cov_params=(0.6443532335067832, 0.08031734039754651), pattern_modifier_params=(29.97218126794771, 4.923396327847095), normalizer_modifier_params=() score=0.343605
cov_params=(0.6627163536499598, 0.028209927871517604), pattern_modifier_params=(29.968970141073424, 4.913478746254578), normalizer_modifier_params=() score=0.368872
cov_params=(0.6637163536499598, 0.028209927871517604), pattern_modifier_params=(29.968970141073424, 4.913478746254578), normalizer_modifier_params=() score=0.368976
cov_params=(0.6627163536499598, 0.029209927871517605), pattern_modifier_params=(29.968970141073424, 4.913478746254578), normalizer_modifier_params=() score=0.368606
cov_params=(0.6627163536499598, 0.028209927871517604), pattern_modifier_params=(29.969970141073425, 4.913478746254578), normalizer_modifier_params=() score=0.368869
cov_params=(0.6627163536499598, 0.028209927871517604), pattern_modifier_params=(29.968970141073424, 4.914478746254578), normalizer_modifier_params=() score=0.368864
cov_params=(0.7670465209893657, 0.0), pattern_modifier_params=(29.96589839861781, 4.9058939152727365), normalizer_modifier_params=() score=0.357881
cov_params=(0.7680465209893657, 0.0), pattern_modifier_params=(29.96589839861781, 4.9058939152727365), normalizer_modifier_params=() score=0.358038
cov_params=(0.7670465209893657, 0.001), pattern_modifier_params=(29.96589839861781, 4.9058939152727365), normalizer_modifier_params=() score=0.361368
cov_params=(0.7670465209893657, 0.0), pattern_modifier_params=(29.96689839861781, 4.9058939152727365), normalizer_modifier_params=() score=0.357875
cov_params=(0.7670465209893657, 0.0), pattern_modifier_params=(29.96589839861781, 4.906893915272737), normalizer_modifier_params=() score=0.357883
cov_params=(0.7048322843401036, 0.016822163456784937), pattern_modifier_params=(29.967730142177057, 4.910416906864553), normalizer_modifier_params=() score=0.373740
cov_params=(0.7058322843401036, 0.016822163456784937), pattern_modifier_params=(29.967730142177057, 4.910416906864553), normalizer_modifier_params=() score=0.373836
cov_params=(0.7048322843401036, 0.017822163456784938), pattern_modifier_params=(29.967730142177057, 4.910416906864553), normalizer_modifier_params=() score=0.373924
cov_params=(0.7048322843401036, 0.016822163456784937), pattern_modifier_params=(29.96873014217706, 4.910416906864553), normalizer_modifier_params=() score=0.373737
cov_params=(0.7048322843401036, 0.016822163456784937), pattern_modifier_params=(29.967730142177057, 4.911416906864553), normalizer_modifier_params=() score=0.373736
cov_params=(0.7540905730693692, 0.013499243030878894), pattern_modifier_params=(29.96626904920268, 4.906920126090405), normalizer_modifier_params=() score=0.377343
cov_params=(0.7550905730693692, 0.013499243030878894), pattern_modifier_params=(29.96626904920268, 4.906920126090405), normalizer_modifier_params=() score=0.377439
cov_params=(0.7540905730693692, 0.014499243030878895), pattern_modifier_params=(29.96626904920268, 4.906920126090405), normalizer_modifier_params=() score=0.377763
cov_params=(0.7540905730693692, 0.013499243030878894), pattern_modifier_params=(29.96726904920268, 4.906920126090405), normalizer_modifier_params=() score=0.377340
cov_params=(0.7540905730693692, 0.013499243030878894), pattern_modifier_params=(29.96626904920268, 4.9079201260904055), normalizer_modifier_params=() score=0.377340
cov_params=(1.0, 0.0), pattern_modifier_params=(29.950171128477027, 4.8686416206840235), normalizer_modifier_params=() score=0.332510
cov_params=(0.999, 0.0), pattern_modifier_params=(29.950171128477027, 4.8686416206840235), normalizer_modifier_params=() score=0.348507
cov_params=(1.0, 0.001), pattern_modifier_params=(29.950171128477027, 4.8686416206840235), normalizer_modifier_params=() score=0.332510
cov_params=(1.0, 0.0), pattern_modifier_params=(29.95117112847703, 4.8686416206840235), normalizer_modifier_params=() score=0.332511
cov_params=(1.0, 0.0), pattern_modifier_params=(29.950171128477027, 4.869641620684024), normalizer_modifier_params=() score=0.332506
cov_params=(0.8526990211647191, 0.008086114212062043), pattern_modifier_params=(29.959813863648666, 4.8915706372129515), normalizer_modifier_params=() score=0.383847
cov_params=(0.8536990211647191, 0.008086114212062043), pattern_modifier_params=(29.959813863648666, 4.8915706372129515), normalizer_modifier_params=() score=0.383957
cov_params=(0.8526990211647191, 0.009086114212062044), pattern_modifier_params=(29.959813863648666, 4.8915706372129515), normalizer_modifier_params=() score=0.384617
cov_params=(0.8526990211647191, 0.008086114212062043), pattern_modifier_params=(29.960813863648667, 4.8915706372129515), normalizer_modifier_params=() score=0.383844
cov_params=(0.8526990211647191, 0.008086114212062043), pattern_modifier_params=(29.959813863648666, 4.892570637212952), normalizer_modifier_params=() score=0.383847
cov_params=(0.9499176671960045, 0.0027492788321010937), pattern_modifier_params=(29.953449658435385, 4.876437486303859), normalizer_modifier_params=() score=0.391218
cov_params=(0.9509176671960045, 0.0027492788321010937), pattern_modifier_params=(29.953449658435385, 4.876437486303859), normalizer_modifier_params=() score=0.391328
cov_params=(0.9499176671960045, 0.0037492788321010937), pattern_modifier_params=(29.953449658435385, 4.876437486303859), normalizer_modifier_params=() score=0.391733
cov_params=(0.9499176671960045, 0.0027492788321010937), pattern_modifier_params=(29.954449658435387, 4.876437486303859), normalizer_modifier_params=() score=0.391214
cov_params=(0.9499176671960045, 0.0027492788321010937), pattern_modifier_params=(29.953449658435385, 4.877437486303859), normalizer_modifier_params=() score=0.391218
cov_params=(0.9803858688101427, 0.0010767213240918862), pattern_modifier_params=(29.951455124511412, 4.871694775807695), normalizer_modifier_params=() score=0.391335
cov_params=(0.9813858688101427, 0.0010767213240918862), pattern_modifier_params=(29.951455124511412, 4.871694775807695), normalizer_modifier_params=() score=0.391090
cov_params=(0.9803858688101427, 0.0020767213240918863), pattern_modifier_params=(29.951455124511412, 4.871694775807695), normalizer_modifier_params=() score=0.391431
cov_params=(0.9803858688101427, 0.0010767213240918862), pattern_modifier_params=(29.952455124511413, 4.871694775807695), normalizer_modifier_params=() score=0.391333
cov_params=(0.9803858688101427, 0.0010767213240918862), pattern_modifier_params=(29.951455124511412, 4.8726947758076955), normalizer_modifier_params=() score=0.391333
cov_params=(0.9574185809282916, 0.002337514798937927), pattern_modifier_params=(29.95295862758659, 4.8752698866293045), normalizer_modifier_params=() score=0.391789
cov_params=(0.9584185809282916, 0.002337514798937927), pattern_modifier_params=(29.95295862758659, 4.8752698866293045), normalizer_modifier_params=() score=0.391879
cov_params=(0.9574185809282916, 0.003337514798937927), pattern_modifier_params=(29.95295862758659, 4.8752698866293045), normalizer_modifier_params=() score=0.392216
cov_params=(0.9574185809282916, 0.002337514798937927), pattern_modifier_params=(29.95395862758659, 4.8752698866293045), normalizer_modifier_params=() score=0.391785
cov_params=(0.9574185809282916, 0.002337514798937927), pattern_modifier_params=(29.95295862758659, 4.876269886629305), normalizer_modifier_params=() score=0.391788
cov_params=(0.9699932528467375, 0.0016472258808617798), pattern_modifier_params=(29.952135454297867, 4.873312500720917), normalizer_modifier_params=() score=0.392297
cov_params=(0.9709932528467375, 0.0016472258808617798), pattern_modifier_params=(29.952135454297867, 4.873312500720917), normalizer_modifier_params=() score=0.392300
cov_params=(0.9699932528467375, 0.00264722588086178), pattern_modifier_params=(29.952135454297867, 4.873312500720917), normalizer_modifier_params=() score=0.392549
cov_params=(0.9699932528467375, 0.0016472258808617798), pattern_modifier_params=(29.95313545429787, 4.873312500720917), normalizer_modifier_params=() score=0.392293
cov_params=(0.9699932528467375, 0.0016472258808617798), pattern_modifier_params=(29.952135454297867, 4.874312500720917), normalizer_modifier_params=() score=0.392295
cov_params=(0.9225231238046329, 0.015211881150587817), pattern_modifier_params=(29.960910155832725, 4.896086572506774), normalizer_modifier_params=() score=0.393809
cov_params=(0.9235231238046329, 0.015211881150587817), pattern_modifier_params=(29.960910155832725, 4.896086572506774), normalizer_modifier_params=() score=0.393880
cov_params=(0.9225231238046329, 0.016211881150587817), pattern_modifier_params=(29.960910155832725, 4.896086572506774), normalizer_modifier_params=() score=0.394013
cov_params=(0.9225231238046329, 0.015211881150587817), pattern_modifier_params=(29.961910155832726, 4.896086572506774), normalizer_modifier_params=() score=0.393807
cov_params=(0.9225231238046329, 0.015211881150587817), pattern_modifier_params=(29.960910155832725, 4.897086572506774), normalizer_modifier_params=() score=0.393808
cov_params=(0.9492204678121738, 0.039092974004306724), pattern_modifier_params=(29.971528400079535, 4.92782219525526), normalizer_modifier_params=() score=0.394942
cov_params=(0.9502204678121738, 0.039092974004306724), pattern_modifier_params=(29.971528400079535, 4.92782219525526), normalizer_modifier_params=() score=0.394960
cov_params=(0.9492204678121738, 0.040092974004306725), pattern_modifier_params=(29.971528400079535, 4.92782219525526), normalizer_modifier_params=() score=0.394828
cov_params=(0.9492204678121738, 0.039092974004306724), pattern_modifier_params=(29.972528400079536, 4.92782219525526), normalizer_modifier_params=() score=0.394941
cov_params=(0.9492204678121738, 0.039092974004306724), pattern_modifier_params=(29.971528400079535, 4.92882219525526), normalizer_modifier_params=() score=0.394939
cov_params=(0.9700451920044341, 0.02829741724845628), pattern_modifier_params=(29.965043913355956, 4.910663919854389), normalizer_modifier_params=() score=0.394539
cov_params=(0.9710451920044341, 0.02829741724845628), pattern_modifier_params=(29.965043913355956, 4.910663919854389), normalizer_modifier_params=() score=0.394370
cov_params=(0.9700451920044341, 0.029297417248456283), pattern_modifier_params=(29.965043913355956, 4.910663919854389), normalizer_modifier_params=() score=0.394510
cov_params=(0.9700451920044341, 0.02829741724845628), pattern_modifier_params=(29.966043913355957, 4.910663919854389), normalizer_modifier_params=() score=0.394538
cov_params=(0.9700451920044341, 0.02829741724845628), pattern_modifier_params=(29.965043913355956, 4.911663919854389), normalizer_modifier_params=() score=0.394537
cov_params=(0.9581116939510036, 0.034483753948152875), pattern_modifier_params=(29.968759814175524, 4.920496378820285), normalizer_modifier_params=() score=0.395324
cov_params=(0.9591116939510036, 0.034483753948152875), pattern_modifier_params=(29.968759814175524, 4.920496378820285), normalizer_modifier_params=() score=0.395284
cov_params=(0.9581116939510036, 0.035483753948152875), pattern_modifier_params=(29.968759814175524, 4.920496378820285), normalizer_modifier_params=() score=0.395252
cov_params=(0.9581116939510036, 0.034483753948152875), pattern_modifier_params=(29.969759814175525, 4.920496378820285), normalizer_modifier_params=() score=0.395323
cov_params=(0.9581116939510036, 0.034483753948152875), pattern_modifier_params=(29.968759814175524, 4.921496378820286), normalizer_modifier_params=() score=0.395321
cov_params=(0.9480406724865438, 0.02056353932381044), pattern_modifier_params=(29.961869988891713, 4.900891609949009), normalizer_modifier_params=() score=0.395698
cov_params=(0.9490406724865438, 0.02056353932381044), pattern_modifier_params=(29.961869988891713, 4.900891609949009), normalizer_modifier_params=() score=0.395708
cov_params=(0.9480406724865438, 0.02156353932381044), pattern_modifier_params=(29.961869988891713, 4.900891609949009), normalizer_modifier_params=() score=0.395756
cov_params=(0.9480406724865438, 0.02056353932381044), pattern_modifier_params=(29.962869988891715, 4.900891609949009), normalizer_modifier_params=() score=0.395696
cov_params=(0.9480406724865438, 0.02056353932381044), pattern_modifier_params=(29.961869988891713, 4.9018916099490095), normalizer_modifier_params=() score=0.395696
cov_params=(0.9503945927129629, 0.026202708718212262), pattern_modifier_params=(29.964469693063545, 4.908585304151802), normalizer_modifier_params=() score=0.395840
cov_params=(0.9513945927129629, 0.026202708718212262), pattern_modifier_params=(29.964469693063545, 4.908585304151802), normalizer_modifier_params=() score=0.395838
cov_params=(0.9503945927129629, 0.027202708718212263), pattern_modifier_params=(29.964469693063545, 4.908585304151802), normalizer_modifier_params=() score=0.395828
cov_params=(0.9503945927129629, 0.026202708718212262), pattern_modifier_params=(29.965469693063547, 4.908585304151802), normalizer_modifier_params=() score=0.395839
cov_params=(0.9503945927129629, 0.026202708718212262), pattern_modifier_params=(29.964469693063545, 4.909585304151802), normalizer_modifier_params=() score=0.395838

Let’s take a look at the optimal parameters:

shrinkage_params = model_opt.cov_params_
pattern_params = model_opt.pattern_modifier_params_
print('Optimal shrinkage parameters:', shrinkage_params)
print('Optimal pattern parameters:', pattern_params)

Out:

Optimal shrinkage parameters: [0.9503945927129629, 0.026202708718212262]
Optimal pattern parameters: [29.964469693063545, 4.908585304151802]

To evaluate the performance of the new model, you can pass the WorkbenchOptimizer object into cross_val_predict(). This would cause the optimization procedure to be run during every iteration of the cross-validation loop. To save time in this example, we are going to do freeze the parameters before entering the model into the cross-validation loop. So take this result with a grain of salt, as the hyperparameters have been tuned using all data, not just the training set!

model = Workbench(
    ols,
    cov=cov_estimators.ShrinkageKernel(alpha=shrinkage_params[0]),
    pattern_modifier=partial(pattern_modifier, mean=pattern_params[0], std=pattern_params[1]),
    normalizer_modifier=normalizers.unit_gain,
)
FAS_pred = cross_val_predict(model, X, y, cv=10)
perf_opt, _ = pearsonr(epochs.metadata['FAS'], FAS_pred)
print(f'Performance: {perf_opt:.2f} (to beat: {perf_naive:.2f})')

Out:

Performance: 0.37 (to beat: 0.30)

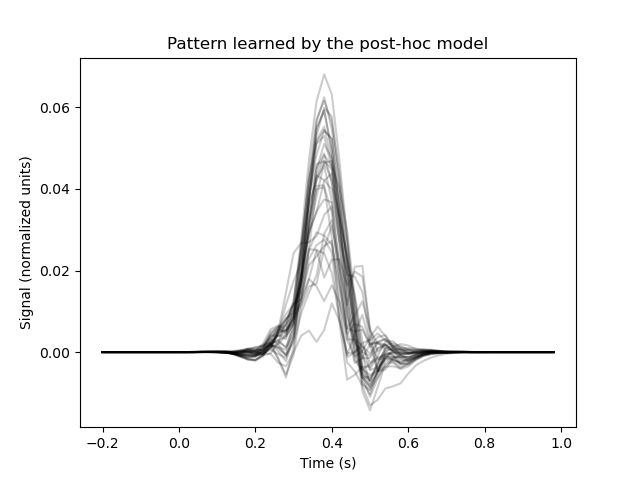
Here is the final pattern:

model.fit(X, y)
plt.figure()
plt.plot(epochs.times, model.pattern_.reshape(32, 60).T, color='black', alpha=0.2)
plt.xlabel('Time (s)')
plt.ylabel('Signal (normalized units)')
plt.title('Pattern learned by the post-hoc model')

Out:

Text(0.5, 1.0, 'Pattern learned by the post-hoc model')

References¶

1: Marijn van Vliet and Riitta Salmelin (2020). Post-hoc modification of linear models: combining machine learning with domain information to make solid inferences from noisy data. Neuroimage, 204, 116221. https://doi.org/10.1016/j.neuroimage.2019.116221

sphinx_gallery_thumbnail_number = 5

Total running time of the script: ( 5 minutes 0.946 seconds)

Gallery generated by Sphinx-Gallery