Note
Go to the end to download the full example code.
Source-level RSA using a searchlight on surface data#
This example demonstrates how to perform representational similarity analysis (RSA) on source localized MEG data, using a searchlight approach.
In the searchlight approach, representational similarity is computed between the model and searchlight “patches”. A patch is defined by a seed vertex on the cortex and all vertices within a given radius. By default, patches are created using each vertex as a seed point, so you can think of it as a “searchlight” that scans along the cortex.
The radius of a searchlight can be defined in space, in time, or both. In this example, our searchlight will have a spatial radius of 2 cm. and a temporal radius of 20 ms.
The dataset will be the MNE-sample dataset: a collection of 288 epochs in which the participant was presented with an auditory beep or visual stimulus to either the left or right ear or visual field.
# sphinx_gallery_thumbnail_number=2
import mne
import mne_rsa
# Import required packages
from matplotlib import pyplot as plt
mne.set_log_level(False) # Be less verbose
mne.viz.set_3d_backend("pyvista")
'pyvistaqt'
We’ll be using the data from the MNE-sample set. To speed up computations in this example, we’re going to use one of the sparse source spaces from the testing set.
sample_root = mne.datasets.sample.data_path(verbose=True)
testing_root = mne.datasets.testing.data_path(verbose=True)
sample_path = sample_root / "MEG" / "sample"
testing_path = testing_root / "MEG" / "sample"
subjects_dir = sample_root / "subjects"
Creating epochs from the continuous (raw) data. We downsample to 100 Hz to speed up the RSA computations later on.
raw = mne.io.read_raw_fif(sample_path / "sample_audvis_filt-0-40_raw.fif")
events = mne.read_events(sample_path / "sample_audvis_filt-0-40_raw-eve.fif")
event_id = {"audio/left": 1, "audio/right": 2, "visual/left": 3, "visual/right": 4}
epochs = mne.Epochs(raw, events, event_id, preload=True)
epochs.resample(100)
It’s important that the model RDM and the epochs are in the same order, so that each row in the model RDM will correspond to an epoch. The model RDM will be easier to interpret visually if the data is ordered such that all epochs belonging to the same experimental condition are right next to each-other, so patterns jump out. This can be achieved by first splitting the epochs by experimental condition and then concatenating them together again.
epoch_splits = [
epochs[cl] for cl in ["audio/left", "audio/right", "visual/left", "visual/right"]
]
epochs = mne.concatenate_epochs(epoch_splits)
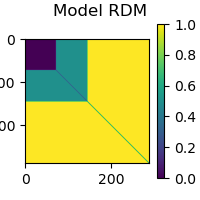
Now that the epochs are in the proper order, we can create a RDM based on the experimental conditions. This type of RDM is referred to as a “sensitivity RDM”. Let’s create a sensitivity RDM that will pick up the left auditory response when RSA-ed against the MEG data. Since we want to capture areas where left beeps generate a large signal, we specify that left beeps should be similar to other left beeps. Since we do not want areas where visual stimuli generate a large signal, we specify that beeps must be different from visual stimuli. Furthermore, since in areas where visual stimuli generate only a small signal, random noise will dominate, we also specify that visual stimuli are different from other visual stimuli. Finally left and right auditory beeps will be somewhat similar.
def sensitivity_metric(event_id_1, event_id_2):
"""Determine similarity between two epochs, given their event ids."""
if event_id_1 == 1 and event_id_2 == 1:
return 0 # Completely similar
if event_id_1 == 2 and event_id_2 == 2:
return 0.5 # Somewhat similar
elif event_id_1 == 1 and event_id_2 == 2:
return 0.5 # Somewhat similar
elif event_id_1 == 2 and event_id_1 == 1:
return 0.5 # Somewhat similar
else:
return 1 # Not similar at all
model_rdm = mne_rsa.compute_rdm(epochs.events[:, 2], metric=sensitivity_metric)
mne_rsa.plot_rdms(model_rdm, title="Model RDM")
<Figure size 200x200 with 2 Axes>
This example is going to be on source-level, so let’s load the inverse operator and apply it to obtain a cortical surface source estimate for each epoch. To speed up the computation, we going to load an inverse operator from the testing dataset that was created using a sparse source space with not too many vertices.
inv = mne.minimum_norm.read_inverse_operator(
testing_path / "sample_audvis_trunc-meg-eeg-oct-4-meg-inv.fif"
)
epochs_stc = mne.minimum_norm.apply_inverse_epochs(epochs, inv, lambda2=0.1111)
Performing the RSA. This will take some time. Consider increasing n_jobs to
parallelize the computation across multiple CPUs.
rsa_vals = mne_rsa.rsa_stcs(
epochs_stc, # The source localized epochs
model_rdm, # The model RDM we constructed above
src=inv["src"], # The inverse operator has our source space
stc_rdm_metric="correlation", # Metric to compute the MEG RDMs
rsa_metric="kendall-tau-a", # Metric to compare model and EEG RDMs
spatial_radius=0.02, # Spatial radius of the searchlight patch
temporal_radius=0.02, # Temporal radius of the searchlight path
tmin=0,
tmax=0.3, # To save time, only analyze this time interval
n_jobs=1, # Only use one CPU core. Increase this for more speed.
verbose=True,
) # Set to True to display a progress bar
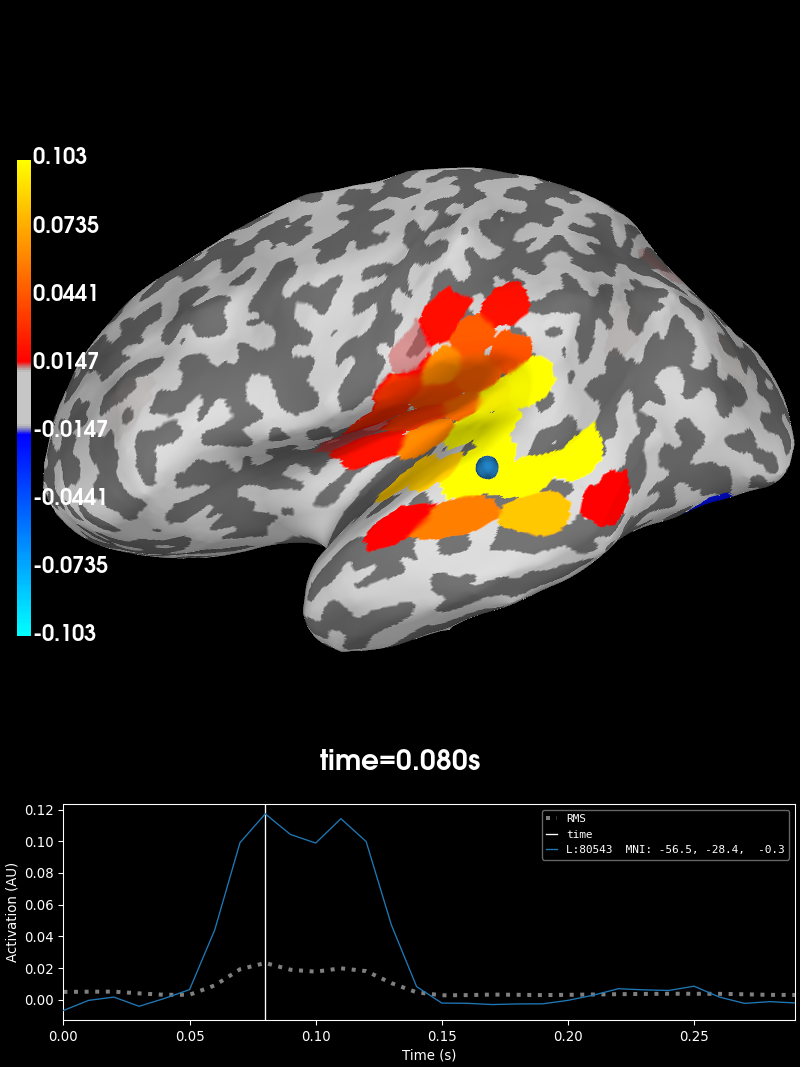
# Find the searchlight patch with highest RSA score
peak_vertex, peak_time = rsa_vals.get_peak(vert_as_index=True)
# Plot the result at the timepoint where the maximum RSA value occurs.
rsa_vals.plot("sample", subjects_dir=subjects_dir, initial_time=peak_time)
Calculating source space distances (limit=20.0 mm)...
Not adding patch information, dist_limit too small
Performing RSA between SourceEstimates and 1 model RDM(s)
Spatial radius: 0.02 meters
Using 498 vertices
Temporal radius: 2 samples
Time interval: 0-0.3 seconds
Number of searchlight patches: 14940
0%| | 0/14940 [00:00<?, ?patch/s]Creating spatio-temporal searchlight patches
0%| | 8/14940 [00:00<03:14, 76.90patch/s]
0%|▏ | 16/14940 [00:00<03:13, 77.00patch/s]
0%|▎ | 25/14940 [00:00<03:09, 78.69patch/s]
0%|▍ | 34/14940 [00:00<03:07, 79.53patch/s]
0%|▍ | 43/14940 [00:00<03:03, 81.35patch/s]
0%|▌ | 52/14940 [00:00<03:06, 79.87patch/s]
0%|▋ | 61/14940 [00:00<03:04, 80.85patch/s]
0%|▊ | 70/14940 [00:00<03:03, 81.17patch/s]
1%|▉ | 79/14940 [00:00<03:05, 80.09patch/s]
1%|▉ | 88/14940 [00:01<03:06, 79.47patch/s]
1%|█ | 96/14940 [00:01<03:09, 78.31patch/s]
1%|█▏ | 104/14940 [00:01<03:08, 78.70patch/s]
1%|█▏ | 113/14940 [00:01<03:07, 79.22patch/s]
1%|█▎ | 122/14940 [00:01<03:03, 80.69patch/s]
1%|█▍ | 131/14940 [00:01<03:05, 79.66patch/s]
1%|█▌ | 139/14940 [00:01<03:07, 78.90patch/s]
1%|█▌ | 147/14940 [00:01<03:09, 77.87patch/s]
1%|█▋ | 155/14940 [00:01<03:11, 77.12patch/s]
1%|█▊ | 164/14940 [00:02<03:08, 78.23patch/s]
1%|█▉ | 172/14940 [00:02<03:08, 78.36patch/s]
1%|█▉ | 181/14940 [00:02<03:05, 79.52patch/s]
1%|██ | 190/14940 [00:02<03:02, 80.66patch/s]
1%|██▏ | 199/14940 [00:02<03:01, 81.05patch/s]
1%|██▎ | 208/14940 [00:02<03:02, 80.70patch/s]
1%|██▍ | 217/14940 [00:02<03:03, 80.41patch/s]
2%|██▍ | 226/14940 [00:02<03:06, 78.89patch/s]
2%|██▌ | 234/14940 [00:02<03:23, 72.36patch/s]
2%|██▋ | 243/14940 [00:03<03:17, 74.53patch/s]
2%|██▊ | 251/14940 [00:03<03:18, 73.99patch/s]
2%|██▊ | 259/14940 [00:03<03:19, 73.46patch/s]
2%|██▉ | 267/14940 [00:03<03:20, 73.36patch/s]
2%|███ | 275/14940 [00:03<03:20, 73.23patch/s]
2%|███▏ | 283/14940 [00:03<03:23, 72.08patch/s]
2%|███▏ | 291/14940 [00:03<03:20, 73.13patch/s]
2%|███▎ | 299/14940 [00:03<03:20, 73.16patch/s]
2%|███▍ | 308/14940 [00:03<03:12, 76.00patch/s]
2%|███▌ | 317/14940 [00:04<03:06, 78.20patch/s]
2%|███▌ | 326/14940 [00:04<03:05, 78.62patch/s]
2%|███▋ | 334/14940 [00:04<03:13, 75.38patch/s]
2%|███▊ | 342/14940 [00:04<03:28, 70.10patch/s]
2%|███▊ | 350/14940 [00:04<03:26, 70.69patch/s]
2%|███▉ | 358/14940 [00:04<03:20, 72.81patch/s]
2%|████ | 366/14940 [00:04<03:26, 70.69patch/s]
3%|████▏ | 374/14940 [00:04<03:31, 68.84patch/s]
3%|████▏ | 381/14940 [00:05<03:33, 68.22patch/s]
3%|████▎ | 388/14940 [00:05<03:34, 67.75patch/s]
3%|████▎ | 395/14940 [00:05<03:34, 67.90patch/s]
3%|████▍ | 403/14940 [00:05<03:26, 70.37patch/s]
3%|████▌ | 412/14940 [00:05<03:16, 73.77patch/s]
3%|████▋ | 420/14940 [00:05<03:17, 73.53patch/s]
3%|████▋ | 429/14940 [00:05<03:10, 76.02patch/s]
3%|████▊ | 438/14940 [00:05<03:05, 78.15patch/s]
3%|████▉ | 447/14940 [00:05<03:00, 80.15patch/s]
3%|█████ | 456/14940 [00:05<02:57, 81.82patch/s]
3%|█████▏ | 465/14940 [00:06<02:54, 82.80patch/s]
3%|█████▏ | 474/14940 [00:06<03:19, 72.53patch/s]
3%|█████▎ | 482/14940 [00:06<03:16, 73.53patch/s]
3%|█████▍ | 491/14940 [00:06<03:09, 76.44patch/s]
3%|█████▌ | 500/14940 [00:06<03:03, 78.56patch/s]
3%|█████▌ | 509/14940 [00:06<03:00, 80.07patch/s]
3%|█████▋ | 518/14940 [00:06<02:58, 80.91patch/s]
4%|█████▊ | 527/14940 [00:06<02:56, 81.51patch/s]
4%|█████▉ | 536/14940 [00:06<02:56, 81.61patch/s]
4%|██████ | 545/14940 [00:07<02:56, 81.58patch/s]
4%|██████ | 554/14940 [00:07<02:55, 82.07patch/s]
4%|██████▏ | 563/14940 [00:07<02:55, 82.11patch/s]
4%|██████▎ | 572/14940 [00:07<02:53, 82.72patch/s]
4%|██████▍ | 581/14940 [00:07<02:52, 83.40patch/s]
4%|██████▌ | 590/14940 [00:07<02:50, 83.93patch/s]
4%|██████▌ | 599/14940 [00:07<02:50, 84.04patch/s]
4%|██████▋ | 608/14940 [00:07<02:49, 84.33patch/s]
4%|██████▊ | 617/14940 [00:07<02:50, 84.22patch/s]
4%|██████▉ | 626/14940 [00:08<02:49, 84.24patch/s]
4%|███████ | 635/14940 [00:08<02:49, 84.50patch/s]
4%|███████ | 644/14940 [00:08<02:49, 84.18patch/s]
4%|███████▏ | 653/14940 [00:08<02:51, 83.33patch/s]
4%|███████▎ | 662/14940 [00:08<02:52, 82.98patch/s]
4%|███████▍ | 671/14940 [00:08<02:51, 82.97patch/s]
5%|███████▌ | 680/14940 [00:08<02:52, 82.81patch/s]
5%|███████▌ | 689/14940 [00:08<02:52, 82.83patch/s]
5%|███████▋ | 698/14940 [00:08<02:51, 82.88patch/s]
5%|███████▊ | 707/14940 [00:09<02:51, 83.00patch/s]
5%|███████▉ | 716/14940 [00:09<02:50, 83.24patch/s]
5%|████████ | 725/14940 [00:09<02:51, 82.73patch/s]
5%|████████ | 734/14940 [00:09<02:50, 83.38patch/s]
5%|████████▏ | 743/14940 [00:09<02:48, 84.10patch/s]
5%|████████▎ | 752/14940 [00:09<02:48, 84.37patch/s]
5%|████████▍ | 761/14940 [00:09<02:48, 84.10patch/s]
5%|████████▌ | 770/14940 [00:09<02:48, 84.17patch/s]
5%|████████▌ | 779/14940 [00:09<02:49, 83.74patch/s]
5%|████████▋ | 788/14940 [00:10<02:50, 83.21patch/s]
5%|████████▊ | 797/14940 [00:10<02:49, 83.67patch/s]
5%|████████▉ | 806/14940 [00:10<02:52, 82.12patch/s]
5%|█████████ | 815/14940 [00:10<02:53, 81.44patch/s]
6%|█████████ | 824/14940 [00:10<02:52, 81.94patch/s]
6%|█████████▏ | 833/14940 [00:10<02:50, 82.97patch/s]
6%|█████████▎ | 842/14940 [00:10<02:50, 82.87patch/s]
6%|█████████▍ | 851/14940 [00:10<02:51, 82.01patch/s]
6%|█████████▍ | 860/14940 [00:10<02:56, 79.77patch/s]
6%|█████████▌ | 868/14940 [00:10<02:57, 79.16patch/s]
6%|█████████▋ | 876/14940 [00:11<02:57, 79.18patch/s]
6%|█████████▊ | 884/14940 [00:11<03:01, 77.28patch/s]
6%|█████████▊ | 893/14940 [00:11<02:58, 78.55patch/s]
6%|█████████▉ | 902/14940 [00:11<02:55, 79.79patch/s]
6%|██████████ | 910/14940 [00:11<02:57, 79.08patch/s]
6%|██████████▏ | 918/14940 [00:11<03:00, 77.76patch/s]
6%|██████████▏ | 926/14940 [00:11<03:06, 75.32patch/s]
6%|██████████▎ | 934/14940 [00:11<03:08, 74.29patch/s]
6%|██████████▍ | 942/14940 [00:11<03:09, 74.01patch/s]
6%|██████████▍ | 950/14940 [00:12<03:08, 74.32patch/s]
6%|██████████▌ | 958/14940 [00:12<03:06, 75.08patch/s]
6%|██████████▋ | 967/14940 [00:12<03:00, 77.35patch/s]
7%|██████████▊ | 975/14940 [00:12<02:59, 77.76patch/s]
7%|██████████▊ | 984/14940 [00:12<02:57, 78.77patch/s]
7%|██████████▉ | 993/14940 [00:12<02:53, 80.39patch/s]
7%|██████████▉ | 1002/14940 [00:12<02:52, 80.94patch/s]
7%|███████████ | 1011/14940 [00:12<02:46, 83.45patch/s]
7%|███████████▏ | 1020/14940 [00:12<02:47, 82.99patch/s]
7%|███████████▎ | 1029/14940 [00:13<02:48, 82.48patch/s]
7%|███████████▍ | 1038/14940 [00:13<02:48, 82.46patch/s]
7%|███████████▍ | 1047/14940 [00:13<03:12, 72.22patch/s]
7%|███████████▌ | 1055/14940 [00:13<03:39, 63.21patch/s]
7%|███████████▋ | 1062/14940 [00:13<03:50, 60.26patch/s]
7%|███████████▋ | 1070/14940 [00:13<03:34, 64.77patch/s]
7%|███████████▊ | 1078/14940 [00:13<03:22, 68.36patch/s]
7%|███████████▉ | 1086/14940 [00:13<03:15, 70.87patch/s]
7%|████████████ | 1094/14940 [00:14<03:10, 72.80patch/s]
7%|████████████ | 1102/14940 [00:14<03:05, 74.64patch/s]
7%|████████████▏ | 1110/14940 [00:14<03:01, 76.01patch/s]
7%|████████████▎ | 1119/14940 [00:14<02:56, 78.29patch/s]
8%|████████████▎ | 1127/14940 [00:14<03:00, 76.67patch/s]
8%|████████████▍ | 1136/14940 [00:14<02:56, 78.03patch/s]
8%|████████████▌ | 1145/14940 [00:14<02:54, 79.25patch/s]
8%|████████████▋ | 1153/14940 [00:14<02:53, 79.34patch/s]
8%|████████████▋ | 1161/14940 [00:14<02:53, 79.23patch/s]
8%|████████████▊ | 1169/14940 [00:14<02:56, 77.81patch/s]
8%|████████████▉ | 1177/14940 [00:15<02:57, 77.54patch/s]
8%|█████████████ | 1185/14940 [00:15<03:26, 66.63patch/s]
8%|█████████████ | 1194/14940 [00:15<03:12, 71.32patch/s]
8%|█████████████▏ | 1202/14940 [00:15<03:07, 73.43patch/s]
8%|█████████████▎ | 1211/14940 [00:15<02:59, 76.50patch/s]
8%|█████████████▍ | 1220/14940 [00:15<02:58, 76.97patch/s]
8%|█████████████▍ | 1228/14940 [00:15<02:56, 77.65patch/s]
8%|█████████████▌ | 1236/14940 [00:15<02:56, 77.44patch/s]
8%|█████████████▋ | 1245/14940 [00:15<02:54, 78.70patch/s]
8%|█████████████▊ | 1254/14940 [00:16<02:50, 80.14patch/s]
8%|█████████████▊ | 1263/14940 [00:16<02:51, 79.81patch/s]
9%|█████████████▉ | 1272/14940 [00:16<02:50, 80.29patch/s]
9%|██████████████ | 1281/14940 [00:16<02:49, 80.64patch/s]
9%|██████████████▏ | 1290/14940 [00:16<02:48, 81.15patch/s]
9%|██████████████▎ | 1299/14940 [00:16<02:47, 81.42patch/s]
9%|██████████████▎ | 1308/14940 [00:16<03:10, 71.72patch/s]
9%|██████████████▍ | 1316/14940 [00:16<03:11, 71.26patch/s]
9%|██████████████▌ | 1325/14940 [00:17<03:03, 74.34patch/s]
9%|██████████████▋ | 1334/14940 [00:17<02:56, 76.96patch/s]
9%|██████████████▋ | 1343/14940 [00:17<02:52, 79.04patch/s]
9%|██████████████▊ | 1352/14940 [00:17<02:49, 80.14patch/s]
9%|██████████████▉ | 1361/14940 [00:17<02:54, 78.03patch/s]
9%|███████████████ | 1369/14940 [00:17<03:04, 73.66patch/s]
9%|███████████████ | 1377/14940 [00:17<03:12, 70.44patch/s]
9%|███████████████▏ | 1385/14940 [00:17<03:21, 67.15patch/s]
9%|███████████████▎ | 1393/14940 [00:17<03:12, 70.34patch/s]
9%|███████████████▍ | 1401/14940 [00:18<03:10, 71.09patch/s]
9%|███████████████▍ | 1409/14940 [00:18<03:04, 73.21patch/s]
9%|███████████████▌ | 1417/14940 [00:18<03:00, 74.79patch/s]
10%|███████████████▋ | 1425/14940 [00:18<03:00, 75.07patch/s]
10%|███████████████▋ | 1433/14940 [00:18<02:58, 75.67patch/s]
10%|███████████████▊ | 1441/14940 [00:18<03:03, 73.64patch/s]
10%|███████████████▉ | 1450/14940 [00:18<03:02, 74.07patch/s]
10%|████████████████ | 1458/14940 [00:18<02:59, 75.04patch/s]
10%|████████████████ | 1466/14940 [00:18<02:57, 76.09patch/s]
10%|████████████████▏ | 1475/14940 [00:19<02:52, 78.11patch/s]
10%|████████████████▎ | 1484/14940 [00:19<02:45, 81.26patch/s]
10%|████████████████▍ | 1493/14940 [00:19<02:42, 82.64patch/s]
10%|████████████████▍ | 1502/14940 [00:19<02:41, 83.34patch/s]
10%|████████████████▌ | 1511/14940 [00:19<02:40, 83.84patch/s]
10%|████████████████▋ | 1520/14940 [00:19<02:40, 83.37patch/s]
10%|████████████████▊ | 1529/14940 [00:19<02:43, 81.78patch/s]
10%|████████████████▉ | 1538/14940 [00:19<02:46, 80.71patch/s]
10%|████████████████▉ | 1547/14940 [00:19<02:46, 80.57patch/s]
10%|█████████████████ | 1556/14940 [00:20<02:46, 80.55patch/s]
10%|█████████████████▏ | 1565/14940 [00:20<02:56, 75.64patch/s]
11%|█████████████████▎ | 1573/14940 [00:20<02:55, 76.18patch/s]
11%|█████████████████▎ | 1581/14940 [00:20<02:53, 77.06patch/s]
11%|█████████████████▍ | 1589/14940 [00:20<02:54, 76.31patch/s]
11%|█████████████████▌ | 1597/14940 [00:20<02:54, 76.64patch/s]
11%|█████████████████▌ | 1605/14940 [00:20<02:54, 76.57patch/s]
11%|█████████████████▋ | 1613/14940 [00:20<03:04, 72.22patch/s]
11%|█████████████████▊ | 1621/14940 [00:20<03:03, 72.60patch/s]
11%|█████████████████▉ | 1629/14940 [00:20<03:00, 73.65patch/s]
11%|█████████████████▉ | 1637/14940 [00:21<03:00, 73.78patch/s]
11%|██████████████████ | 1645/14940 [00:21<03:01, 73.17patch/s]
11%|██████████████████▏ | 1653/14940 [00:21<03:06, 71.09patch/s]
11%|██████████████████▏ | 1661/14940 [00:21<03:06, 71.13patch/s]
11%|██████████████████▎ | 1669/14940 [00:21<03:02, 72.58patch/s]
11%|██████████████████▍ | 1678/14940 [00:21<02:56, 75.23patch/s]
11%|██████████████████▌ | 1686/14940 [00:21<03:01, 73.20patch/s]
11%|██████████████████▌ | 1694/14940 [00:21<03:01, 73.15patch/s]
11%|██████████████████▋ | 1702/14940 [00:21<02:58, 74.03patch/s]
11%|██████████████████▊ | 1711/14940 [00:22<02:53, 76.03patch/s]
12%|██████████████████▉ | 1720/14940 [00:22<02:50, 77.75patch/s]
12%|██████████████████▉ | 1728/14940 [00:22<03:02, 72.38patch/s]
12%|███████████████████ | 1736/14940 [00:22<02:57, 74.21patch/s]
12%|███████████████████▏ | 1745/14940 [00:22<02:50, 77.30patch/s]
12%|███████████████████▎ | 1754/14940 [00:22<02:46, 79.06patch/s]
12%|███████████████████▎ | 1763/14940 [00:22<02:44, 79.93patch/s]
12%|███████████████████▍ | 1772/14940 [00:22<02:44, 79.84patch/s]
12%|███████████████████▌ | 1781/14940 [00:23<02:48, 78.29patch/s]
12%|███████████████████▋ | 1789/14940 [00:23<02:47, 78.50patch/s]
12%|███████████████████▋ | 1797/14940 [00:23<02:46, 78.72patch/s]
12%|███████████████████▊ | 1805/14940 [00:23<02:46, 79.07patch/s]
12%|███████████████████▉ | 1814/14940 [00:23<02:44, 79.62patch/s]
12%|████████████████████ | 1822/14940 [00:23<02:45, 79.50patch/s]
12%|████████████████████ | 1831/14940 [00:23<02:43, 79.96patch/s]
12%|████████████████████▏ | 1840/14940 [00:23<02:41, 81.01patch/s]
12%|████████████████████▎ | 1849/14940 [00:23<02:50, 77.00patch/s]
12%|████████████████████▍ | 1858/14940 [00:23<02:46, 78.57patch/s]
12%|████████████████████▍ | 1867/14940 [00:24<02:43, 79.96patch/s]
13%|████████████████████▌ | 1876/14940 [00:24<02:41, 80.97patch/s]
13%|████████████████████▋ | 1885/14940 [00:24<02:40, 81.31patch/s]
13%|████████████████████▊ | 1894/14940 [00:24<02:50, 76.71patch/s]
13%|████████████████████▉ | 1902/14940 [00:24<02:57, 73.29patch/s]
13%|████████████████████▉ | 1910/14940 [00:24<03:01, 71.86patch/s]
13%|█████████████████████ | 1918/14940 [00:24<03:24, 63.55patch/s]
13%|█████████████████████▏ | 1925/14940 [00:24<03:23, 63.94patch/s]
13%|█████████████████████▏ | 1933/14940 [00:25<03:16, 66.19patch/s]
13%|█████████████████████▎ | 1941/14940 [00:25<03:08, 68.93patch/s]
13%|█████████████████████▍ | 1949/14940 [00:25<03:01, 71.57patch/s]
13%|█████████████████████▍ | 1957/14940 [00:25<02:57, 73.31patch/s]
13%|█████████████████████▌ | 1966/14940 [00:25<02:51, 75.52patch/s]
13%|█████████████████████▋ | 1974/14940 [00:25<02:50, 76.21patch/s]
13%|█████████████████████▊ | 1983/14940 [00:25<02:43, 79.15patch/s]
13%|█████████████████████▊ | 1992/14940 [00:25<02:42, 79.48patch/s]
13%|█████████████████████▉ | 2000/14940 [00:25<02:56, 73.43patch/s]
13%|██████████████████████ | 2008/14940 [00:26<03:04, 70.25patch/s]
13%|██████████████████████▏ | 2016/14940 [00:26<02:58, 72.34patch/s]
14%|██████████████████████▏ | 2025/14940 [00:26<02:51, 75.16patch/s]
14%|██████████████████████▎ | 2033/14940 [00:26<02:49, 76.11patch/s]
14%|██████████████████████▍ | 2042/14940 [00:26<02:45, 77.88patch/s]
14%|██████████████████████▌ | 2051/14940 [00:26<02:45, 77.94patch/s]
14%|██████████████████████▌ | 2059/14940 [00:26<02:47, 76.88patch/s]
14%|██████████████████████▋ | 2068/14940 [00:26<02:44, 78.43patch/s]
14%|██████████████████████▊ | 2077/14940 [00:26<02:41, 79.77patch/s]
14%|██████████████████████▉ | 2086/14940 [00:27<02:39, 80.63patch/s]
14%|██████████████████████▉ | 2095/14940 [00:27<02:43, 78.51patch/s]
14%|███████████████████████ | 2104/14940 [00:27<02:41, 79.57patch/s]
14%|███████████████████████▏ | 2113/14940 [00:27<02:39, 80.46patch/s]
14%|███████████████████████▎ | 2122/14940 [00:27<02:35, 82.26patch/s]
14%|███████████████████████▍ | 2131/14940 [00:27<02:33, 83.30patch/s]
14%|███████████████████████▍ | 2140/14940 [00:27<02:33, 83.60patch/s]
14%|███████████████████████▌ | 2149/14940 [00:27<02:32, 83.65patch/s]
14%|███████████████████████▋ | 2158/14940 [00:27<02:39, 80.21patch/s]
15%|███████████████████████▊ | 2167/14940 [00:28<02:41, 79.26patch/s]
15%|███████████████████████▉ | 2175/14940 [00:28<02:41, 79.19patch/s]
15%|███████████████████████▉ | 2183/14940 [00:28<02:41, 79.19patch/s]
15%|████████████████████████ | 2192/14940 [00:28<02:40, 79.52patch/s]
15%|████████████████████████▏ | 2201/14940 [00:28<02:37, 80.71patch/s]
15%|████████████████████████▎ | 2210/14940 [00:28<02:34, 82.30patch/s]
15%|████████████████████████▎ | 2219/14940 [00:28<02:34, 82.58patch/s]
15%|████████████████████████▍ | 2228/14940 [00:28<02:33, 82.61patch/s]
15%|████████████████████████▌ | 2237/14940 [00:28<02:34, 82.13patch/s]
15%|████████████████████████▋ | 2246/14940 [00:28<02:34, 82.23patch/s]
15%|████████████████████████▊ | 2255/14940 [00:29<02:33, 82.37patch/s]
15%|████████████████████████▊ | 2264/14940 [00:29<02:34, 82.23patch/s]
15%|████████████████████████▉ | 2273/14940 [00:29<02:33, 82.61patch/s]
15%|█████████████████████████ | 2282/14940 [00:29<02:33, 82.31patch/s]
15%|█████████████████████████▏ | 2291/14940 [00:29<02:34, 81.69patch/s]
15%|█████████████████████████▏ | 2300/14940 [00:29<02:36, 80.72patch/s]
15%|█████████████████████████▎ | 2309/14940 [00:29<02:36, 80.75patch/s]
16%|█████████████████████████▍ | 2318/14940 [00:29<02:37, 80.33patch/s]
16%|█████████████████████████▌ | 2327/14940 [00:29<02:37, 80.20patch/s]
16%|█████████████████████████▋ | 2336/14940 [00:30<02:37, 79.82patch/s]
16%|█████████████████████████▋ | 2344/14940 [00:30<02:41, 78.19patch/s]
16%|█████████████████████████▊ | 2353/14940 [00:30<02:38, 79.57patch/s]
16%|█████████████████████████▉ | 2362/14940 [00:30<02:35, 80.73patch/s]
16%|██████████████████████████ | 2371/14940 [00:30<02:34, 81.49patch/s]
16%|██████████████████████████▏ | 2380/14940 [00:30<02:33, 81.66patch/s]
16%|██████████████████████████▏ | 2389/14940 [00:30<02:43, 76.83patch/s]
16%|██████████████████████████▎ | 2397/14940 [00:30<02:43, 76.84patch/s]
16%|██████████████████████████▍ | 2405/14940 [00:30<02:43, 76.68patch/s]
16%|██████████████████████████▍ | 2413/14940 [00:31<02:43, 76.77patch/s]
16%|██████████████████████████▌ | 2421/14940 [00:31<02:42, 77.22patch/s]
16%|██████████████████████████▋ | 2429/14940 [00:31<02:41, 77.63patch/s]
16%|██████████████████████████▊ | 2437/14940 [00:31<02:43, 76.66patch/s]
16%|██████████████████████████▊ | 2445/14940 [00:31<02:44, 76.10patch/s]
16%|██████████████████████████▉ | 2454/14940 [00:31<02:38, 78.74patch/s]
16%|███████████████████████████ | 2463/14940 [00:31<02:36, 79.65patch/s]
17%|███████████████████████████▏ | 2472/14940 [00:31<02:34, 80.73patch/s]
17%|███████████████████████████▏ | 2481/14940 [00:31<02:36, 79.70patch/s]
17%|███████████████████████████▎ | 2489/14940 [00:32<02:37, 78.85patch/s]
17%|███████████████████████████▍ | 2497/14940 [00:32<02:41, 77.06patch/s]
17%|███████████████████████████▍ | 2505/14940 [00:32<02:43, 76.05patch/s]
17%|███████████████████████████▌ | 2513/14940 [00:32<02:48, 73.77patch/s]
17%|███████████████████████████▋ | 2521/14940 [00:32<02:50, 72.95patch/s]
17%|███████████████████████████▊ | 2529/14940 [00:32<02:45, 74.86patch/s]
17%|███████████████████████████▊ | 2537/14940 [00:32<02:46, 74.63patch/s]
17%|███████████████████████████▉ | 2545/14940 [00:32<02:47, 73.94patch/s]
17%|████████████████████████████ | 2553/14940 [00:32<02:47, 73.91patch/s]
17%|████████████████████████████ | 2561/14940 [00:33<02:52, 71.74patch/s]
17%|████████████████████████████▏ | 2569/14940 [00:33<02:49, 72.91patch/s]
17%|████████████████████████████▎ | 2577/14940 [00:33<02:45, 74.48patch/s]
17%|████████████████████████████▍ | 2586/14940 [00:33<02:41, 76.51patch/s]
17%|████████████████████████████▍ | 2595/14940 [00:33<02:38, 77.96patch/s]
17%|████████████████████████████▌ | 2604/14940 [00:33<02:36, 78.58patch/s]
17%|████████████████████████████▋ | 2613/14940 [00:33<02:36, 78.93patch/s]
18%|████████████████████████████▊ | 2622/14940 [00:33<02:33, 79.99patch/s]
18%|████████████████████████████▉ | 2631/14940 [00:33<02:34, 79.50patch/s]
18%|████████████████████████████▉ | 2639/14940 [00:34<02:40, 76.55patch/s]
18%|█████████████████████████████ | 2648/14940 [00:34<02:39, 77.17patch/s]
18%|█████████████████████████████▏ | 2657/14940 [00:34<02:36, 78.51patch/s]
18%|█████████████████████████████▎ | 2666/14940 [00:34<02:35, 79.11patch/s]
18%|█████████████████████████████▎ | 2675/14940 [00:34<02:33, 79.78patch/s]
18%|█████████████████████████████▍ | 2684/14940 [00:34<02:32, 80.17patch/s]
18%|█████████████████████████████▌ | 2693/14940 [00:34<02:32, 80.08patch/s]
18%|█████████████████████████████▋ | 2702/14940 [00:34<02:32, 80.33patch/s]
18%|█████████████████████████████▊ | 2711/14940 [00:34<02:32, 80.31patch/s]
18%|█████████████████████████████▊ | 2720/14940 [00:35<02:30, 81.24patch/s]
18%|█████████████████████████████▉ | 2729/14940 [00:35<02:44, 74.01patch/s]
18%|██████████████████████████████ | 2738/14940 [00:35<02:41, 75.64patch/s]
18%|██████████████████████████████▏ | 2746/14940 [00:35<02:39, 76.42patch/s]
18%|██████████████████████████████▏ | 2755/14940 [00:35<02:37, 77.56patch/s]
19%|██████████████████████████████▎ | 2764/14940 [00:35<02:35, 78.46patch/s]
19%|██████████████████████████████▍ | 2773/14940 [00:35<02:33, 79.11patch/s]
19%|██████████████████████████████▌ | 2782/14940 [00:35<02:31, 80.12patch/s]
19%|██████████████████████████████▋ | 2791/14940 [00:35<02:33, 78.99patch/s]
19%|██████████████████████████████▋ | 2800/14940 [00:36<02:31, 80.06patch/s]
19%|██████████████████████████████▊ | 2809/14940 [00:36<02:32, 79.63patch/s]
19%|██████████████████████████████▉ | 2818/14940 [00:36<02:31, 79.87patch/s]
19%|███████████████████████████████ | 2826/14940 [00:36<02:32, 79.65patch/s]
19%|███████████████████████████████ | 2834/14940 [00:36<02:31, 79.74patch/s]
19%|███████████████████████████████▏ | 2843/14940 [00:36<02:30, 80.28patch/s]
19%|███████████████████████████████▎ | 2852/14940 [00:36<02:28, 81.18patch/s]
19%|███████████████████████████████▍ | 2861/14940 [00:36<02:27, 82.03patch/s]
19%|███████████████████████████████▌ | 2870/14940 [00:36<02:26, 82.63patch/s]
19%|███████████████████████████████▌ | 2879/14940 [00:37<02:27, 81.55patch/s]
19%|███████████████████████████████▋ | 2888/14940 [00:37<02:26, 82.54patch/s]
19%|███████████████████████████████▊ | 2897/14940 [00:37<02:24, 83.27patch/s]
19%|███████████████████████████████▉ | 2906/14940 [00:37<02:23, 83.83patch/s]
20%|███████████████████████████████▉ | 2915/14940 [00:37<02:22, 84.19patch/s]
20%|████████████████████████████████ | 2924/14940 [00:37<02:22, 84.27patch/s]
20%|████████████████████████████████▏ | 2933/14940 [00:37<02:22, 84.37patch/s]
20%|████████████████████████████████▎ | 2942/14940 [00:37<02:22, 84.17patch/s]
20%|████████████████████████████████▍ | 2951/14940 [00:37<02:25, 82.33patch/s]
20%|████████████████████████████████▍ | 2960/14940 [00:38<02:25, 82.13patch/s]
20%|████████████████████████████████▌ | 2969/14940 [00:38<02:30, 79.57patch/s]
20%|████████████████████████████████▋ | 2977/14940 [00:38<02:36, 76.64patch/s]
20%|████████████████████████████████▊ | 2986/14940 [00:38<02:33, 77.83patch/s]
20%|████████████████████████████████▊ | 2994/14940 [00:38<02:35, 76.58patch/s]
20%|████████████████████████████████▉ | 3002/14940 [00:38<02:36, 76.33patch/s]
20%|█████████████████████████████████ | 3010/14940 [00:38<02:36, 76.12patch/s]
20%|█████████████████████████████████▏ | 3019/14940 [00:38<02:33, 77.45patch/s]
20%|█████████████████████████████████▏ | 3027/14940 [00:38<02:39, 74.49patch/s]
20%|█████████████████████████████████▎ | 3035/14940 [00:39<02:45, 71.76patch/s]
20%|█████████████████████████████████▍ | 3043/14940 [00:39<02:41, 73.89patch/s]
20%|█████████████████████████████████▍ | 3051/14940 [00:39<02:39, 74.34patch/s]
20%|█████████████████████████████████▌ | 3059/14940 [00:39<02:41, 73.74patch/s]
21%|█████████████████████████████████▋ | 3067/14940 [00:39<02:40, 73.92patch/s]
21%|█████████████████████████████████▊ | 3075/14940 [00:39<02:41, 73.63patch/s]
21%|█████████████████████████████████▊ | 3083/14940 [00:39<02:38, 74.79patch/s]
21%|█████████████████████████████████▉ | 3091/14940 [00:39<02:37, 75.16patch/s]
21%|██████████████████████████████████ | 3099/14940 [00:39<02:43, 72.26patch/s]
21%|██████████████████████████████████ | 3107/14940 [00:40<02:43, 72.30patch/s]
21%|██████████████████████████████████▏ | 3115/14940 [00:40<02:40, 73.67patch/s]
21%|██████████████████████████████████▎ | 3123/14940 [00:40<02:38, 74.33patch/s]
21%|██████████████████████████████████▎ | 3131/14940 [00:40<02:36, 75.42patch/s]
21%|██████████████████████████████████▍ | 3139/14940 [00:40<02:39, 74.00patch/s]
21%|██████████████████████████████████▌ | 3147/14940 [00:40<02:42, 72.62patch/s]
21%|██████████████████████████████████▋ | 3155/14940 [00:40<02:41, 72.85patch/s]
21%|██████████████████████████████████▋ | 3163/14940 [00:40<02:40, 73.29patch/s]
21%|██████████████████████████████████▊ | 3171/14940 [00:40<02:38, 74.37patch/s]
21%|██████████████████████████████████▉ | 3179/14940 [00:40<02:36, 75.15patch/s]
21%|██████████████████████████████████▉ | 3187/14940 [00:41<02:46, 70.71patch/s]
21%|███████████████████████████████████ | 3195/14940 [00:41<02:42, 72.34patch/s]
21%|███████████████████████████████████▏ | 3203/14940 [00:41<02:38, 73.87patch/s]
21%|███████████████████████████████████▏ | 3211/14940 [00:41<02:36, 74.96patch/s]
22%|███████████████████████████████████▎ | 3219/14940 [00:41<02:36, 74.81patch/s]
22%|███████████████████████████████████▍ | 3227/14940 [00:41<02:36, 75.03patch/s]
22%|███████████████████████████████████▌ | 3235/14940 [00:41<02:35, 75.08patch/s]
22%|███████████████████████████████████▌ | 3244/14940 [00:41<02:32, 76.80patch/s]
22%|███████████████████████████████████▋ | 3252/14940 [00:41<02:35, 75.16patch/s]
22%|███████████████████████████████████▊ | 3260/14940 [00:42<02:44, 71.18patch/s]
22%|███████████████████████████████████▊ | 3268/14940 [00:42<02:57, 65.80patch/s]
22%|███████████████████████████████████▉ | 3275/14940 [00:42<02:55, 66.48patch/s]
22%|████████████████████████████████████ | 3283/14940 [00:42<02:51, 68.05patch/s]
22%|████████████████████████████████████▏ | 3291/14940 [00:42<02:43, 71.18patch/s]
22%|████████████████████████████████████▏ | 3299/14940 [00:42<02:42, 71.78patch/s]
22%|████████████████████████████████████▎ | 3308/14940 [00:42<02:35, 74.65patch/s]
22%|████████████████████████████████████▍ | 3317/14940 [00:42<02:31, 76.64patch/s]
22%|████████████████████████████████████▍ | 3325/14940 [00:42<02:32, 75.98patch/s]
22%|████████████████████████████████████▌ | 3333/14940 [00:43<02:31, 76.49patch/s]
22%|████████████████████████████████████▋ | 3342/14940 [00:43<02:27, 78.72patch/s]
22%|████████████████████████████████████▊ | 3351/14940 [00:43<02:24, 80.01patch/s]
22%|████████████████████████████████████▉ | 3360/14940 [00:43<02:24, 80.36patch/s]
23%|████████████████████████████████████▉ | 3369/14940 [00:43<02:22, 81.18patch/s]
23%|█████████████████████████████████████ | 3378/14940 [00:43<02:24, 79.95patch/s]
23%|█████████████████████████████████████▏ | 3387/14940 [00:43<02:22, 81.19patch/s]
23%|█████████████████████████████████████▎ | 3396/14940 [00:43<02:21, 81.30patch/s]
23%|█████████████████████████████████████▍ | 3405/14940 [00:43<02:22, 80.77patch/s]
23%|█████████████████████████████████████▍ | 3414/14940 [00:44<02:21, 81.66patch/s]
23%|█████████████████████████████████████▌ | 3423/14940 [00:44<02:23, 80.54patch/s]
23%|█████████████████████████████████████▋ | 3432/14940 [00:44<02:23, 80.44patch/s]
23%|█████████████████████████████████████▊ | 3441/14940 [00:44<02:21, 81.29patch/s]
23%|█████████████████████████████████████▊ | 3450/14940 [00:44<02:20, 81.88patch/s]
23%|█████████████████████████████████████▉ | 3459/14940 [00:44<02:19, 82.12patch/s]
23%|██████████████████████████████████████ | 3468/14940 [00:44<02:19, 82.43patch/s]
23%|██████████████████████████████████████▏ | 3477/14940 [00:44<02:18, 83.01patch/s]
23%|██████████████████████████████████████▎ | 3486/14940 [00:44<02:17, 83.46patch/s]
23%|██████████████████████████████████████▎ | 3495/14940 [00:45<02:16, 83.72patch/s]
23%|██████████████████████████████████████▍ | 3504/14940 [00:45<02:16, 83.98patch/s]
24%|██████████████████████████████████████▌ | 3513/14940 [00:45<02:16, 83.69patch/s]
24%|██████████████████████████████████████▋ | 3522/14940 [00:45<02:16, 83.87patch/s]
24%|██████████████████████████████████████▊ | 3531/14940 [00:45<02:17, 83.15patch/s]
24%|██████████████████████████████████████▊ | 3540/14940 [00:45<02:19, 81.52patch/s]
24%|██████████████████████████████████████▉ | 3549/14940 [00:45<02:19, 81.58patch/s]
24%|███████████████████████████████████████ | 3558/14940 [00:45<02:18, 82.13patch/s]
24%|███████████████████████████████████████▏ | 3567/14940 [00:45<02:18, 82.15patch/s]
24%|███████████████████████████████████████▎ | 3576/14940 [00:46<02:17, 82.38patch/s]
24%|███████████████████████████████████████▎ | 3585/14940 [00:46<02:17, 82.73patch/s]
24%|███████████████████████████████████████▍ | 3594/14940 [00:46<02:17, 82.25patch/s]
24%|███████████████████████████████████████▌ | 3603/14940 [00:46<02:18, 81.95patch/s]
24%|███████████████████████████████████████▋ | 3612/14940 [00:46<02:17, 82.12patch/s]
24%|███████████████████████████████████████▋ | 3621/14940 [00:46<02:17, 82.18patch/s]
24%|███████████████████████████████████████▊ | 3630/14940 [00:46<02:17, 82.42patch/s]
24%|███████████████████████████████████████▉ | 3639/14940 [00:46<02:18, 81.45patch/s]
24%|████████████████████████████████████████ | 3648/14940 [00:46<02:19, 81.10patch/s]
24%|████████████████████████████████████████▏ | 3657/14940 [00:47<02:23, 78.84patch/s]
25%|████████████████████████████████████████▏ | 3666/14940 [00:47<02:21, 79.60patch/s]
25%|████████████████████████████████████████▎ | 3675/14940 [00:47<02:20, 80.34patch/s]
25%|████████████████████████████████████████▍ | 3684/14940 [00:47<02:19, 80.92patch/s]
25%|████████████████████████████████████████▌ | 3693/14940 [00:47<02:18, 81.34patch/s]
25%|████████████████████████████████████████▋ | 3702/14940 [00:47<02:19, 80.53patch/s]
25%|████████████████████████████████████████▋ | 3711/14940 [00:47<02:24, 77.78patch/s]
25%|████████████████████████████████████████▊ | 3720/14940 [00:47<02:23, 78.14patch/s]
25%|████████████████████████████████████████▉ | 3728/14940 [00:47<02:26, 76.66patch/s]
25%|█████████████████████████████████████████ | 3736/14940 [00:48<02:27, 76.01patch/s]
25%|█████████████████████████████████████████ | 3744/14940 [00:48<02:25, 77.04patch/s]
25%|█████████████████████████████████████████▏ | 3753/14940 [00:48<02:21, 78.87patch/s]
25%|█████████████████████████████████████████▎ | 3762/14940 [00:48<02:19, 79.92patch/s]
25%|█████████████████████████████████████████▍ | 3771/14940 [00:48<02:19, 80.35patch/s]
25%|█████████████████████████████████████████▍ | 3780/14940 [00:48<02:17, 81.23patch/s]
25%|█████████████████████████████████████████▌ | 3789/14940 [00:48<02:16, 81.46patch/s]
25%|█████████████████████████████████████████▋ | 3798/14940 [00:48<02:17, 81.16patch/s]
25%|█████████████████████████████████████████▊ | 3807/14940 [00:48<02:17, 81.03patch/s]
26%|█████████████████████████████████████████▉ | 3816/14940 [00:49<02:16, 81.49patch/s]
26%|█████████████████████████████████████████▉ | 3825/14940 [00:49<02:16, 81.61patch/s]
26%|██████████████████████████████████████████ | 3834/14940 [00:49<02:15, 81.76patch/s]
26%|██████████████████████████████████████████▏ | 3843/14940 [00:49<02:16, 81.53patch/s]
26%|██████████████████████████████████████████▎ | 3852/14940 [00:49<02:16, 81.24patch/s]
26%|██████████████████████████████████████████▍ | 3861/14940 [00:49<02:15, 81.52patch/s]
26%|██████████████████████████████████████████▍ | 3870/14940 [00:49<02:15, 81.57patch/s]
26%|██████████████████████████████████████████▌ | 3879/14940 [00:49<02:16, 80.79patch/s]
26%|██████████████████████████████████████████▋ | 3888/14940 [00:49<02:32, 72.63patch/s]
26%|██████████████████████████████████████████▊ | 3897/14940 [00:50<02:26, 75.13patch/s]
26%|██████████████████████████████████████████▉ | 3906/14940 [00:50<02:23, 76.79patch/s]
26%|██████████████████████████████████████████▉ | 3914/14940 [00:50<02:22, 77.28patch/s]
26%|███████████████████████████████████████████ | 3922/14940 [00:50<02:25, 75.77patch/s]
26%|███████████████████████████████████████████▏ | 3930/14940 [00:50<02:33, 71.91patch/s]
26%|███████████████████████████████████████████▏ | 3938/14940 [00:50<02:46, 66.06patch/s]
26%|███████████████████████████████████████████▎ | 3945/14940 [00:50<02:47, 65.84patch/s]
26%|███████████████████████████████████████████▍ | 3952/14940 [00:50<02:46, 66.09patch/s]
26%|███████████████████████████████████████████▍ | 3959/14940 [00:50<02:43, 67.01patch/s]
27%|███████████████████████████████████████████▌ | 3968/14940 [00:51<02:33, 71.26patch/s]
27%|███████████████████████████████████████████▋ | 3976/14940 [00:51<02:38, 69.20patch/s]
27%|███████████████████████████████████████████▋ | 3983/14940 [00:51<02:50, 64.18patch/s]
27%|███████████████████████████████████████████▊ | 3990/14940 [00:51<02:56, 62.06patch/s]
27%|███████████████████████████████████████████▉ | 3998/14940 [00:51<02:44, 66.52patch/s]
27%|███████████████████████████████████████████▉ | 4006/14940 [00:51<02:37, 69.32patch/s]
27%|████████████████████████████████████████████ | 4015/14940 [00:51<02:29, 73.31patch/s]
27%|████████████████████████████████████████████▏ | 4023/14940 [00:51<02:25, 75.00patch/s]
27%|████████████████████████████████████████████▏ | 4031/14940 [00:52<02:38, 68.98patch/s]
27%|████████████████████████████████████████████▎ | 4039/14940 [00:52<02:49, 64.39patch/s]
27%|████████████████████████████████████████████▍ | 4046/14940 [00:52<02:47, 65.21patch/s]
27%|████████████████████████████████████████████▌ | 4054/14940 [00:52<02:38, 68.63patch/s]
27%|████████████████████████████████████████████▌ | 4062/14940 [00:52<02:33, 70.79patch/s]
27%|████████████████████████████████████████████▋ | 4071/14940 [00:52<02:27, 73.93patch/s]
27%|████████████████████████████████████████████▊ | 4079/14940 [00:52<02:24, 75.31patch/s]
27%|████████████████████████████████████████████▊ | 4087/14940 [00:52<02:23, 75.49patch/s]
27%|████████████████████████████████████████████▉ | 4096/14940 [00:52<02:20, 77.24patch/s]
27%|█████████████████████████████████████████████ | 4105/14940 [00:53<02:17, 78.52patch/s]
28%|█████████████████████████████████████████████▏ | 4113/14940 [00:53<02:18, 77.89patch/s]
28%|█████████████████████████████████████████████▏ | 4121/14940 [00:53<02:18, 77.98patch/s]
28%|█████████████████████████████████████████████▎ | 4130/14940 [00:53<02:15, 79.49patch/s]
28%|█████████████████████████████████████████████▍ | 4139/14940 [00:53<02:14, 80.41patch/s]
28%|█████████████████████████████████████████████▌ | 4148/14940 [00:53<02:15, 79.40patch/s]
28%|█████████████████████████████████████████████▋ | 4157/14940 [00:53<02:14, 80.11patch/s]
28%|█████████████████████████████████████████████▋ | 4166/14940 [00:53<02:12, 81.09patch/s]
28%|█████████████████████████████████████████████▊ | 4175/14940 [00:53<02:11, 81.94patch/s]
28%|█████████████████████████████████████████████▉ | 4184/14940 [00:53<02:14, 80.26patch/s]
28%|██████████████████████████████████████████████ | 4193/14940 [00:54<02:12, 81.04patch/s]
28%|██████████████████████████████████████████████▏ | 4202/14940 [00:54<02:12, 81.17patch/s]
28%|██████████████████████████████████████████████▏ | 4211/14940 [00:54<02:11, 81.65patch/s]
28%|██████████████████████████████████████████████▎ | 4220/14940 [00:54<02:11, 81.64patch/s]
28%|██████████████████████████████████████████████▍ | 4229/14940 [00:54<02:10, 81.77patch/s]
28%|██████████████████████████████████████████████▌ | 4238/14940 [00:54<02:10, 82.01patch/s]
28%|██████████████████████████████████████████████▌ | 4247/14940 [00:54<02:09, 82.49patch/s]
28%|██████████████████████████████████████████████▋ | 4256/14940 [00:54<02:09, 82.46patch/s]
29%|██████████████████████████████████████████████▊ | 4265/14940 [00:54<02:09, 82.18patch/s]
29%|██████████████████████████████████████████████▉ | 4274/14940 [00:55<02:24, 73.76patch/s]
29%|███████████████████████████████████████████████ | 4282/14940 [00:55<02:21, 75.19patch/s]
29%|███████████████████████████████████████████████ | 4291/14940 [00:55<02:18, 76.73patch/s]
29%|███████████████████████████████████████████████▏ | 4299/14940 [00:55<02:29, 71.41patch/s]
29%|███████████████████████████████████████████████▎ | 4307/14940 [00:55<02:26, 72.48patch/s]
29%|███████████████████████████████████████████████▎ | 4315/14940 [00:55<02:23, 74.01patch/s]
29%|███████████████████████████████████████████████▍ | 4324/14940 [00:55<02:18, 76.49patch/s]
29%|███████████████████████████████████████████████▌ | 4333/14940 [00:55<02:16, 77.95patch/s]
29%|███████████████████████████████████████████████▋ | 4342/14940 [00:56<02:14, 78.92patch/s]
29%|███████████████████████████████████████████████▊ | 4351/14940 [00:56<02:12, 79.78patch/s]
29%|███████████████████████████████████████████████▊ | 4360/14940 [00:56<02:11, 80.21patch/s]
29%|███████████████████████████████████████████████▉ | 4369/14940 [00:56<02:11, 80.43patch/s]
29%|████████████████████████████████████████████████ | 4378/14940 [00:56<02:10, 80.77patch/s]
29%|████████████████████████████████████████████████▏ | 4387/14940 [00:56<02:08, 81.84patch/s]
29%|████████████████████████████████████████████████▎ | 4396/14940 [00:56<02:08, 81.94patch/s]
29%|████████████████████████████████████████████████▎ | 4405/14940 [00:56<02:07, 82.78patch/s]
30%|████████████████████████████████████████████████▍ | 4414/14940 [00:56<02:06, 83.49patch/s]
30%|████████████████████████████████████████████████▌ | 4423/14940 [00:56<02:06, 83.00patch/s]
30%|████████████████████████████████████████████████▋ | 4432/14940 [00:57<02:11, 79.63patch/s]
30%|████████████████████████████████████████████████▋ | 4441/14940 [00:57<02:10, 80.22patch/s]
30%|████████████████████████████████████████████████▊ | 4450/14940 [00:57<02:09, 81.10patch/s]
30%|████████████████████████████████████████████████▉ | 4459/14940 [00:57<02:08, 81.31patch/s]
30%|█████████████████████████████████████████████████ | 4468/14940 [00:57<02:07, 81.90patch/s]
30%|█████████████████████████████████████████████████▏ | 4477/14940 [00:57<02:07, 82.09patch/s]
30%|█████████████████████████████████████████████████▏ | 4486/14940 [00:57<02:07, 82.10patch/s]
30%|█████████████████████████████████████████████████▎ | 4495/14940 [00:57<02:07, 82.18patch/s]
30%|█████████████████████████████████████████████████▍ | 4504/14940 [00:57<02:06, 82.29patch/s]
30%|█████████████████████████████████████████████████▌ | 4513/14940 [00:58<02:06, 82.70patch/s]
30%|█████████████████████████████████████████████████▋ | 4522/14940 [00:58<02:05, 83.11patch/s]
30%|█████████████████████████████████████████████████▋ | 4531/14940 [00:58<02:04, 83.28patch/s]
30%|█████████████████████████████████████████████████▊ | 4540/14940 [00:58<02:08, 81.15patch/s]
30%|█████████████████████████████████████████████████▉ | 4549/14940 [00:58<02:07, 81.23patch/s]
31%|██████████████████████████████████████████████████ | 4558/14940 [00:58<02:09, 80.19patch/s]
31%|██████████████████████████████████████████████████▏ | 4567/14940 [00:58<02:08, 80.52patch/s]
31%|██████████████████████████████████████████████████▏ | 4576/14940 [00:58<02:07, 81.22patch/s]
31%|██████████████████████████████████████████████████▎ | 4585/14940 [00:58<02:08, 80.51patch/s]
31%|██████████████████████████████████████████████████▍ | 4594/14940 [00:59<02:07, 81.22patch/s]
31%|██████████████████████████████████████████████████▌ | 4603/14940 [00:59<02:06, 81.59patch/s]
31%|██████████████████████████████████████████████████▋ | 4612/14940 [00:59<02:11, 78.60patch/s]
31%|██████████████████████████████████████████████████▋ | 4620/14940 [00:59<02:25, 71.17patch/s]
31%|██████████████████████████████████████████████████▊ | 4628/14940 [00:59<02:23, 71.81patch/s]
31%|██████████████████████████████████████████████████▉ | 4636/14940 [00:59<02:27, 70.04patch/s]
31%|██████████████████████████████████████████████████▉ | 4644/14940 [00:59<02:47, 61.44patch/s]
31%|███████████████████████████████████████████████████ | 4652/14940 [00:59<02:36, 65.75patch/s]
31%|███████████████████████████████████████████████████▏ | 4661/14940 [01:00<02:25, 70.41patch/s]
31%|███████████████████████████████████████████████████▎ | 4669/14940 [01:00<02:21, 72.70patch/s]
31%|███████████████████████████████████████████████████▎ | 4677/14940 [01:00<02:17, 74.60patch/s]
31%|███████████████████████████████████████████████████▍ | 4686/14940 [01:00<02:13, 76.87patch/s]
31%|███████████████████████████████████████████████████▌ | 4695/14940 [01:00<02:09, 79.19patch/s]
31%|███████████████████████████████████████████████████▋ | 4704/14940 [01:00<02:06, 80.99patch/s]
32%|███████████████████████████████████████████████████▋ | 4713/14940 [01:00<02:02, 83.31patch/s]
32%|███████████████████████████████████████████████████▊ | 4722/14940 [01:00<02:11, 77.63patch/s]
32%|███████████████████████████████████████████████████▉ | 4730/14940 [01:00<02:22, 71.44patch/s]
32%|████████████████████████████████████████████████████ | 4738/14940 [01:01<02:20, 72.45patch/s]
32%|████████████████████████████████████████████████████ | 4747/14940 [01:01<02:16, 74.65patch/s]
32%|████████████████████████████████████████████████████▏ | 4756/14940 [01:01<02:12, 76.58patch/s]
32%|████████████████████████████████████████████████████▎ | 4764/14940 [01:01<02:11, 77.36patch/s]
32%|████████████████████████████████████████████████████▍ | 4772/14940 [01:01<02:10, 77.66patch/s]
32%|████████████████████████████████████████████████████▍ | 4780/14940 [01:01<02:12, 76.74patch/s]
32%|████████████████████████████████████████████████████▌ | 4788/14940 [01:01<02:13, 75.80patch/s]
32%|████████████████████████████████████████████████████▋ | 4796/14940 [01:01<02:12, 76.71patch/s]
32%|████████████████████████████████████████████████████▋ | 4804/14940 [01:01<02:12, 76.64patch/s]
32%|████████████████████████████████████████████████████▊ | 4812/14940 [01:02<02:13, 75.78patch/s]
32%|████████████████████████████████████████████████████▉ | 4821/14940 [01:02<02:10, 77.70patch/s]
32%|█████████████████████████████████████████████████████ | 4830/14940 [01:02<02:08, 78.86patch/s]
32%|█████████████████████████████████████████████████████ | 4838/14940 [01:02<02:12, 76.39patch/s]
32%|█████████████████████████████████████████████████████▏ | 4846/14940 [01:02<02:12, 76.14patch/s]
32%|█████████████████████████████████████████████████████▎ | 4854/14940 [01:02<02:19, 72.14patch/s]
33%|█████████████████████████████████████████████████████▎ | 4862/14940 [01:02<02:18, 72.74patch/s]
33%|█████████████████████████████████████████████████████▍ | 4870/14940 [01:02<02:17, 73.12patch/s]
33%|█████████████████████████████████████████████████████▌ | 4878/14940 [01:02<02:21, 70.89patch/s]
33%|█████████████████████████████████████████████████████▋ | 4886/14940 [01:03<02:19, 72.28patch/s]
33%|█████████████████████████████████████████████████████▋ | 4894/14940 [01:03<02:23, 70.24patch/s]
33%|█████████████████████████████████████████████████████▊ | 4902/14940 [01:03<02:22, 70.28patch/s]
33%|█████████████████████████████████████████████████████▉ | 4910/14940 [01:03<02:18, 72.19patch/s]
33%|█████████████████████████████████████████████████████▉ | 4918/14940 [01:03<02:15, 74.11patch/s]
33%|██████████████████████████████████████████████████████ | 4927/14940 [01:03<02:11, 76.12patch/s]
33%|██████████████████████████████████████████████████████▏ | 4936/14940 [01:03<02:09, 77.50patch/s]
33%|██████████████████████████████████████████████████████▎ | 4944/14940 [01:03<02:31, 65.92patch/s]
33%|██████████████████████████████████████████████████████▎ | 4952/14940 [01:03<02:24, 68.97patch/s]
33%|██████████████████████████████████████████████████████▍ | 4960/14940 [01:04<02:21, 70.35patch/s]
33%|██████████████████████████████████████████████████████▌ | 4968/14940 [01:04<02:20, 71.18patch/s]
33%|██████████████████████████████████████████████████████▌ | 4976/14940 [01:04<02:18, 71.73patch/s]
33%|██████████████████████████████████████████████████████▋ | 4984/14940 [01:04<02:23, 69.47patch/s]
33%|██████████████████████████████████████████████████████▊ | 4992/14940 [01:04<02:26, 68.03patch/s]
33%|██████████████████████████████████████████████████████▉ | 4999/14940 [01:04<02:48, 59.14patch/s]
34%|██████████████████████████████████████████████████████▉ | 5007/14940 [01:04<02:37, 62.96patch/s]
34%|███████████████████████████████████████████████████████ | 5015/14940 [01:04<02:28, 66.83patch/s]
34%|███████████████████████████████████████████████████████▏ | 5023/14940 [01:05<02:22, 69.40patch/s]
34%|███████████████████████████████████████████████████████▏ | 5031/14940 [01:05<02:18, 71.59patch/s]
34%|███████████████████████████████████████████████████████▎ | 5039/14940 [01:05<02:14, 73.40patch/s]
34%|███████████████████████████████████████████████████████▍ | 5047/14940 [01:05<02:11, 75.14patch/s]
34%|███████████████████████████████████████████████████████▍ | 5055/14940 [01:05<02:10, 75.92patch/s]
34%|███████████████████████████████████████████████████████▌ | 5063/14940 [01:05<02:10, 75.68patch/s]
34%|███████████████████████████████████████████████████████▋ | 5071/14940 [01:05<02:08, 76.76patch/s]
34%|███████████████████████████████████████████████████████▊ | 5079/14940 [01:05<02:17, 71.57patch/s]
34%|███████████████████████████████████████████████████████▊ | 5087/14940 [01:05<02:17, 71.63patch/s]
34%|███████████████████████████████████████████████████████▉ | 5095/14940 [01:05<02:15, 72.83patch/s]
34%|████████████████████████████████████████████████████████ | 5103/14940 [01:06<02:17, 71.64patch/s]
34%|████████████████████████████████████████████████████████ | 5112/14940 [01:06<02:11, 74.97patch/s]
34%|████████████████████████████████████████████████████████▏ | 5120/14940 [01:06<02:08, 76.30patch/s]
34%|████████████████████████████████████████████████████████▎ | 5129/14940 [01:06<02:06, 77.44patch/s]
34%|████████████████████████████████████████████████████████▍ | 5137/14940 [01:06<02:05, 78.14patch/s]
34%|████████████████████████████████████████████████████████▍ | 5145/14940 [01:06<02:09, 75.88patch/s]
34%|████████████████████████████████████████████████████████▌ | 5153/14940 [01:06<02:21, 69.06patch/s]
35%|████████████████████████████████████████████████████████▋ | 5161/14940 [01:06<02:22, 68.54patch/s]
35%|████████████████████████████████████████████████████████▋ | 5169/14940 [01:07<02:18, 70.73patch/s]
35%|████████████████████████████████████████████████████████▊ | 5177/14940 [01:07<02:16, 71.34patch/s]
35%|████████████████████████████████████████████████████████▉ | 5186/14940 [01:07<02:10, 74.86patch/s]
35%|█████████████████████████████████████████████████████████ | 5195/14940 [01:07<02:06, 77.17patch/s]
35%|█████████████████████████████████████████████████████████▏ | 5204/14940 [01:07<02:05, 77.74patch/s]
35%|█████████████████████████████████████████████████████████▏ | 5213/14940 [01:07<02:02, 79.63patch/s]
35%|█████████████████████████████████████████████████████████▎ | 5222/14940 [01:07<02:02, 79.45patch/s]
35%|█████████████████████████████████████████████████████████▍ | 5231/14940 [01:07<02:00, 80.85patch/s]
35%|█████████████████████████████████████████████████████████▌ | 5240/14940 [01:07<01:58, 82.07patch/s]
35%|█████████████████████████████████████████████████████████▌ | 5249/14940 [01:07<01:58, 81.66patch/s]
35%|█████████████████████████████████████████████████████████▋ | 5258/14940 [01:08<01:59, 81.35patch/s]
35%|█████████████████████████████████████████████████████████▊ | 5267/14940 [01:08<02:02, 79.15patch/s]
35%|█████████████████████████████████████████████████████████▉ | 5276/14940 [01:08<02:00, 79.99patch/s]
35%|██████████████████████████████████████████████████████████ | 5285/14940 [01:08<02:01, 79.30patch/s]
35%|██████████████████████████████████████████████████████████ | 5294/14940 [01:08<02:00, 79.95patch/s]
35%|██████████████████████████████████████████████████████████▏ | 5303/14940 [01:08<02:01, 79.11patch/s]
36%|██████████████████████████████████████████████████████████▎ | 5312/14940 [01:08<02:00, 80.07patch/s]
36%|██████████████████████████████████████████████████████████▍ | 5321/14940 [01:08<02:00, 80.14patch/s]
36%|██████████████████████████████████████████████████████████▌ | 5330/14940 [01:09<01:58, 81.13patch/s]
36%|██████████████████████████████████████████████████████████▌ | 5339/14940 [01:09<01:58, 80.80patch/s]
36%|██████████████████████████████████████████████████████████▋ | 5348/14940 [01:09<01:59, 80.45patch/s]
36%|██████████████████████████████████████████████████████████▊ | 5357/14940 [01:09<01:58, 81.16patch/s]
36%|██████████████████████████████████████████████████████████▉ | 5366/14940 [01:09<01:57, 81.66patch/s]
36%|███████████████████████████████████████████████████████████ | 5375/14940 [01:09<01:56, 82.18patch/s]
36%|███████████████████████████████████████████████████████████ | 5384/14940 [01:09<01:57, 81.04patch/s]
36%|███████████████████████████████████████████████████████████▏ | 5393/14940 [01:09<01:57, 81.59patch/s]
36%|███████████████████████████████████████████████████████████▎ | 5402/14940 [01:09<01:57, 81.32patch/s]
36%|███████████████████████████████████████████████████████████▍ | 5411/14940 [01:09<01:57, 81.29patch/s]
36%|███████████████████████████████████████████████████████████▍ | 5420/14940 [01:10<02:02, 77.46patch/s]
36%|███████████████████████████████████████████████████████████▌ | 5429/14940 [01:10<02:00, 78.72patch/s]
36%|███████████████████████████████████████████████████████████▋ | 5438/14940 [01:10<01:58, 79.90patch/s]
36%|███████████████████████████████████████████████████████████▊ | 5447/14940 [01:10<01:58, 79.81patch/s]
37%|███████████████████████████████████████████████████████████▉ | 5456/14940 [01:10<02:04, 76.31patch/s]
37%|███████████████████████████████████████████████████████████▉ | 5464/14940 [01:10<02:09, 72.98patch/s]
37%|████████████████████████████████████████████████████████████ | 5472/14940 [01:10<02:10, 72.35patch/s]
37%|████████████████████████████████████████████████████████████▏ | 5481/14940 [01:10<02:05, 75.44patch/s]
37%|████████████████████████████████████████████████████████████▎ | 5489/14940 [01:11<02:03, 76.65patch/s]
37%|████████████████████████████████████████████████████████████▎ | 5498/14940 [01:11<02:01, 77.81patch/s]
37%|████████████████████████████████████████████████████████████▍ | 5507/14940 [01:11<01:58, 79.27patch/s]
37%|████████████████████████████████████████████████████████████▌ | 5516/14940 [01:11<01:57, 80.16patch/s]
37%|████████████████████████████████████████████████████████████▋ | 5525/14940 [01:11<01:56, 81.12patch/s]
37%|████████████████████████████████████████████████████████████▋ | 5534/14940 [01:11<01:54, 81.98patch/s]
37%|████████████████████████████████████████████████████████████▊ | 5543/14940 [01:11<01:53, 82.79patch/s]
37%|████████████████████████████████████████████████████████████▉ | 5552/14940 [01:11<01:54, 81.71patch/s]
37%|█████████████████████████████████████████████████████████████ | 5561/14940 [01:11<01:58, 79.06patch/s]
37%|█████████████████████████████████████████████████████████████▏ | 5569/14940 [01:12<02:12, 70.62patch/s]
37%|█████████████████████████████████████████████████████████████▏ | 5577/14940 [01:12<02:13, 70.28patch/s]
37%|█████████████████████████████████████████████████████████████▎ | 5585/14940 [01:12<02:10, 71.73patch/s]
37%|█████████████████████████████████████████████████████████████▍ | 5594/14940 [01:12<02:04, 75.26patch/s]
38%|█████████████████████████████████████████████████████████████▌ | 5603/14940 [01:12<02:00, 77.60patch/s]
38%|█████████████████████████████████████████████████████████████▌ | 5611/14940 [01:12<02:05, 74.04patch/s]
38%|█████████████████████████████████████████████████████████████▋ | 5619/14940 [01:12<02:03, 75.49patch/s]
38%|█████████████████████████████████████████████████████████████▊ | 5628/14940 [01:12<02:00, 77.42patch/s]
38%|█████████████████████████████████████████████████████████████▉ | 5637/14940 [01:12<01:58, 78.44patch/s]
38%|█████████████████████████████████████████████████████████████▉ | 5646/14940 [01:13<01:56, 79.75patch/s]
38%|██████████████████████████████████████████████████████████████ | 5655/14940 [01:13<01:54, 80.75patch/s]
38%|██████████████████████████████████████████████████████████████▏ | 5664/14940 [01:13<01:54, 81.28patch/s]
38%|██████████████████████████████████████████████████████████████▎ | 5673/14940 [01:13<01:53, 81.75patch/s]
38%|██████████████████████████████████████████████████████████████▎ | 5682/14940 [01:13<01:52, 82.26patch/s]
38%|██████████████████████████████████████████████████████████████▍ | 5691/14940 [01:13<01:54, 81.02patch/s]
38%|██████████████████████████████████████████████████████████████▌ | 5700/14940 [01:13<01:52, 81.79patch/s]
38%|██████████████████████████████████████████████████████████████▋ | 5709/14940 [01:13<01:50, 83.19patch/s]
38%|██████████████████████████████████████████████████████████████▊ | 5718/14940 [01:13<01:49, 84.00patch/s]
38%|██████████████████████████████████████████████████████████████▊ | 5727/14940 [01:14<01:48, 84.62patch/s]
38%|██████████████████████████████████████████████████████████████▉ | 5736/14940 [01:14<01:49, 84.33patch/s]
38%|███████████████████████████████████████████████████████████████ | 5745/14940 [01:14<01:49, 84.15patch/s]
39%|███████████████████████████████████████████████████████████████▏ | 5754/14940 [01:14<01:48, 84.64patch/s]
39%|███████████████████████████████████████████████████████████████▎ | 5763/14940 [01:14<01:47, 85.24patch/s]
39%|███████████████████████████████████████████████████████████████▎ | 5772/14940 [01:14<01:48, 84.30patch/s]
39%|███████████████████████████████████████████████████████████████▍ | 5781/14940 [01:14<01:49, 83.89patch/s]
39%|███████████████████████████████████████████████████████████████▌ | 5790/14940 [01:14<01:49, 83.39patch/s]
39%|███████████████████████████████████████████████████████████████▋ | 5799/14940 [01:14<01:50, 82.57patch/s]
39%|███████████████████████████████████████████████████████████████▊ | 5808/14940 [01:14<01:50, 82.55patch/s]
39%|███████████████████████████████████████████████████████████████▊ | 5817/14940 [01:15<01:56, 78.31patch/s]
39%|███████████████████████████████████████████████████████████████▉ | 5826/14940 [01:15<01:54, 79.28patch/s]
39%|████████████████████████████████████████████████████████████████ | 5835/14940 [01:15<01:53, 80.29patch/s]
39%|████████████████████████████████████████████████████████████████▏ | 5844/14940 [01:15<01:54, 79.18patch/s]
39%|████████████████████████████████████████████████████████████████▏ | 5852/14940 [01:15<01:55, 78.92patch/s]
39%|████████████████████████████████████████████████████████████████▎ | 5860/14940 [01:15<01:59, 75.99patch/s]
39%|████████████████████████████████████████████████████████████████▍ | 5868/14940 [01:15<02:00, 75.19patch/s]
39%|████████████████████████████████████████████████████████████████▌ | 5876/14940 [01:15<02:02, 74.25patch/s]
39%|████████████████████████████████████████████████████████████████▌ | 5885/14940 [01:16<01:57, 76.97patch/s]
39%|████████████████████████████████████████████████████████████████▋ | 5894/14940 [01:16<01:55, 78.38patch/s]
40%|████████████████████████████████████████████████████████████████▊ | 5903/14940 [01:16<02:04, 72.80patch/s]
40%|████████████████████████████████████████████████████████████████▉ | 5912/14940 [01:16<01:59, 75.78patch/s]
40%|████████████████████████████████████████████████████████████████▉ | 5921/14940 [01:16<01:55, 77.78patch/s]
40%|█████████████████████████████████████████████████████████████████ | 5929/14940 [01:16<01:56, 77.46patch/s]
40%|█████████████████████████████████████████████████████████████████▏ | 5938/14940 [01:16<01:54, 78.89patch/s]
40%|█████████████████████████████████████████████████████████████████▎ | 5947/14940 [01:16<01:52, 79.81patch/s]
40%|█████████████████████████████████████████████████████████████████▍ | 5956/14940 [01:16<01:51, 80.81patch/s]
40%|█████████████████████████████████████████████████████████████████▍ | 5965/14940 [01:17<01:50, 81.38patch/s]
40%|█████████████████████████████████████████████████████████████████▌ | 5974/14940 [01:17<01:49, 81.66patch/s]
40%|█████████████████████████████████████████████████████████████████▋ | 5983/14940 [01:17<01:49, 82.09patch/s]
40%|█████████████████████████████████████████████████████████████████▊ | 5992/14940 [01:17<01:48, 82.45patch/s]
40%|█████████████████████████████████████████████████████████████████▊ | 6001/14940 [01:17<01:48, 82.38patch/s]
40%|█████████████████████████████████████████████████████████████████▉ | 6010/14940 [01:17<01:52, 79.69patch/s]
40%|██████████████████████████████████████████████████████████████████ | 6018/14940 [01:17<01:52, 79.58patch/s]
40%|██████████████████████████████████████████████████████████████████▏ | 6027/14940 [01:17<01:50, 80.33patch/s]
40%|██████████████████████████████████████████████████████████████████▎ | 6036/14940 [01:17<01:53, 78.58patch/s]
40%|██████████████████████████████████████████████████████████████████▎ | 6045/14940 [01:18<01:51, 79.47patch/s]
41%|██████████████████████████████████████████████████████████████████▍ | 6053/14940 [01:18<01:52, 79.29patch/s]
41%|██████████████████████████████████████████████████████████████████▌ | 6062/14940 [01:18<01:52, 79.15patch/s]
41%|██████████████████████████████████████████████████████████████████▋ | 6071/14940 [01:18<01:50, 80.41patch/s]
41%|██████████████████████████████████████████████████████████████████▋ | 6080/14940 [01:18<01:48, 81.43patch/s]
41%|██████████████████████████████████████████████████████████████████▊ | 6089/14940 [01:18<01:47, 82.33patch/s]
41%|██████████████████████████████████████████████████████████████████▉ | 6098/14940 [01:18<01:46, 82.89patch/s]
41%|███████████████████████████████████████████████████████████████████ | 6107/14940 [01:18<01:46, 82.86patch/s]
41%|███████████████████████████████████████████████████████████████████▏ | 6116/14940 [01:18<01:47, 82.37patch/s]
41%|███████████████████████████████████████████████████████████████████▏ | 6125/14940 [01:19<01:59, 73.57patch/s]
41%|███████████████████████████████████████████████████████████████████▎ | 6133/14940 [01:19<02:00, 73.33patch/s]
41%|███████████████████████████████████████████████████████████████████▍ | 6141/14940 [01:19<01:59, 73.78patch/s]
41%|███████████████████████████████████████████████████████████████████▍ | 6149/14940 [01:19<01:58, 74.07patch/s]
41%|███████████████████████████████████████████████████████████████████▌ | 6157/14940 [01:19<01:56, 75.43patch/s]
41%|███████████████████████████████████████████████████████████████████▋ | 6165/14940 [01:19<01:56, 75.36patch/s]
41%|███████████████████████████████████████████████████████████████████▊ | 6173/14940 [01:19<01:57, 74.54patch/s]
41%|███████████████████████████████████████████████████████████████████▊ | 6182/14940 [01:19<01:54, 76.40patch/s]
41%|███████████████████████████████████████████████████████████████████▉ | 6191/14940 [01:19<01:51, 78.20patch/s]
41%|████████████████████████████████████████████████████████████████████ | 6200/14940 [01:20<01:49, 79.56patch/s]
42%|████████████████████████████████████████████████████████████████████▏ | 6208/14940 [01:20<01:55, 75.43patch/s]
42%|████████████████████████████████████████████████████████████████████▏ | 6216/14940 [01:20<02:02, 71.19patch/s]
42%|████████████████████████████████████████████████████████████████████▎ | 6224/14940 [01:20<01:59, 72.88patch/s]
42%|████████████████████████████████████████████████████████████████████▍ | 6232/14940 [01:20<01:56, 74.77patch/s]
42%|████████████████████████████████████████████████████████████████████▌ | 6241/14940 [01:20<01:53, 76.56patch/s]
42%|████████████████████████████████████████████████████████████████████▌ | 6250/14940 [01:20<01:51, 78.23patch/s]
42%|████████████████████████████████████████████████████████████████████▋ | 6259/14940 [01:20<01:49, 79.01patch/s]
42%|████████████████████████████████████████████████████████████████████▊ | 6268/14940 [01:20<01:49, 79.45patch/s]
42%|████████████████████████████████████████████████████████████████████▉ | 6277/14940 [01:21<01:48, 79.75patch/s]
42%|█████████████████████████████████████████████████████████████████████ | 6286/14940 [01:21<01:47, 80.50patch/s]
42%|█████████████████████████████████████████████████████████████████████ | 6295/14940 [01:21<01:45, 81.64patch/s]
42%|█████████████████████████████████████████████████████████████████████▏ | 6304/14940 [01:21<01:45, 82.13patch/s]
42%|█████████████████████████████████████████████████████████████████████▎ | 6313/14940 [01:21<01:44, 82.75patch/s]
42%|█████████████████████████████████████████████████████████████████████▍ | 6322/14940 [01:21<01:43, 82.95patch/s]
42%|█████████████████████████████████████████████████████████████████████▍ | 6331/14940 [01:21<01:48, 79.12patch/s]
42%|█████████████████████████████████████████████████████████████████████▌ | 6340/14940 [01:21<01:47, 80.23patch/s]
42%|█████████████████████████████████████████████████████████████████████▋ | 6349/14940 [01:21<01:46, 80.77patch/s]
43%|█████████████████████████████████████████████████████████████████████▊ | 6358/14940 [01:22<01:48, 78.86patch/s]
43%|█████████████████████████████████████████████████████████████████████▉ | 6366/14940 [01:22<01:51, 76.79patch/s]
43%|█████████████████████████████████████████████████████████████████████▉ | 6374/14940 [01:22<01:51, 76.81patch/s]
43%|██████████████████████████████████████████████████████████████████████ | 6382/14940 [01:22<01:50, 77.52patch/s]
43%|██████████████████████████████████████████████████████████████████████▏ | 6391/14940 [01:22<01:48, 78.52patch/s]
43%|██████████████████████████████████████████████████████████████████████▏ | 6399/14940 [01:22<01:49, 78.30patch/s]
43%|██████████████████████████████████████████████████████████████████████▎ | 6408/14940 [01:22<01:46, 80.05patch/s]
43%|██████████████████████████████████████████████████████████████████████▍ | 6417/14940 [01:22<01:46, 79.83patch/s]
43%|██████████████████████████████████████████████████████████████████████▌ | 6425/14940 [01:22<01:49, 77.41patch/s]
43%|██████████████████████████████████████████████████████████████████████▌ | 6433/14940 [01:22<01:50, 76.90patch/s]
43%|██████████████████████████████████████████████████████████████████████▋ | 6441/14940 [01:23<01:55, 73.53patch/s]
43%|██████████████████████████████████████████████████████████████████████▊ | 6449/14940 [01:23<01:57, 72.19patch/s]
43%|██████████████████████████████████████████████████████████████████████▉ | 6458/14940 [01:23<01:53, 74.53patch/s]
43%|██████████████████████████████████████████████████████████████████████▉ | 6466/14940 [01:23<01:52, 75.58patch/s]
43%|███████████████████████████████████████████████████████████████████████ | 6474/14940 [01:23<01:54, 74.10patch/s]
43%|███████████████████████████████████████████████████████████████████████▏ | 6482/14940 [01:23<01:53, 74.48patch/s]
43%|███████████████████████████████████████████████████████████████████████▎ | 6491/14940 [01:23<01:50, 76.56patch/s]
44%|███████████████████████████████████████████████████████████████████████▎ | 6499/14940 [01:23<01:51, 75.40patch/s]
44%|███████████████████████████████████████████████████████████████████████▍ | 6507/14940 [01:23<01:52, 75.20patch/s]
44%|███████████████████████████████████████████████████████████████████████▌ | 6515/14940 [01:24<01:51, 75.89patch/s]
44%|███████████████████████████████████████████████████████████████████████▌ | 6523/14940 [01:24<01:52, 74.83patch/s]
44%|███████████████████████████████████████████████████████████████████████▋ | 6531/14940 [01:24<01:52, 74.69patch/s]
44%|███████████████████████████████████████████████████████████████████████▊ | 6539/14940 [01:24<01:51, 75.35patch/s]
44%|███████████████████████████████████████████████████████████████████████▊ | 6547/14940 [01:24<01:49, 76.56patch/s]
44%|███████████████████████████████████████████████████████████████████████▉ | 6555/14940 [01:24<01:48, 77.34patch/s]
44%|████████████████████████████████████████████████████████████████████████ | 6564/14940 [01:24<01:46, 78.62patch/s]
44%|████████████████████████████████████████████████████████████████████████▏ | 6572/14940 [01:24<01:46, 78.91patch/s]
44%|████████████████████████████████████████████████████████████████████████▏ | 6581/14940 [01:24<01:44, 79.83patch/s]
44%|████████████████████████████████████████████████████████████████████████▎ | 6590/14940 [01:25<01:42, 81.23patch/s]
44%|████████████████████████████████████████████████████████████████████████▍ | 6599/14940 [01:25<01:47, 77.63patch/s]
44%|████████████████████████████████████████████████████████████████████████▌ | 6607/14940 [01:25<01:46, 78.27patch/s]
44%|████████████████████████████████████████████████████████████████████████▋ | 6616/14940 [01:25<01:45, 78.90patch/s]
44%|████████████████████████████████████████████████████████████████████████▋ | 6625/14940 [01:25<01:43, 80.20patch/s]
44%|████████████████████████████████████████████████████████████████████████▊ | 6634/14940 [01:25<01:44, 79.35patch/s]
44%|████████████████████████████████████████████████████████████████████████▉ | 6642/14940 [01:25<01:45, 78.88patch/s]
45%|████████████████████████████████████████████████████████████████████████▉ | 6650/14940 [01:25<01:46, 77.85patch/s]
45%|█████████████████████████████████████████████████████████████████████████ | 6658/14940 [01:25<01:45, 78.17patch/s]
45%|█████████████████████████████████████████████████████████████████████████▏ | 6667/14940 [01:26<01:44, 79.18patch/s]
45%|█████████████████████████████████████████████████████████████████████████▎ | 6675/14940 [01:26<01:50, 75.01patch/s]
45%|█████████████████████████████████████████████████████████████████████████▎ | 6683/14940 [01:26<01:51, 73.97patch/s]
45%|█████████████████████████████████████████████████████████████████████████▍ | 6692/14940 [01:26<01:47, 76.43patch/s]
45%|█████████████████████████████████████████████████████████████████████████▌ | 6701/14940 [01:26<01:45, 78.27patch/s]
45%|█████████████████████████████████████████████████████████████████████████▋ | 6710/14940 [01:26<01:43, 79.37patch/s]
45%|█████████████████████████████████████████████████████████████████████████▊ | 6719/14940 [01:26<01:41, 80.86patch/s]
45%|█████████████████████████████████████████████████████████████████████████▊ | 6728/14940 [01:26<01:40, 82.04patch/s]
45%|█████████████████████████████████████████████████████████████████████████▉ | 6737/14940 [01:26<01:40, 81.89patch/s]
45%|██████████████████████████████████████████████████████████████████████████ | 6746/14940 [01:27<01:40, 81.92patch/s]
45%|██████████████████████████████████████████████████████████████████████████▏ | 6755/14940 [01:27<01:40, 81.54patch/s]
45%|██████████████████████████████████████████████████████████████████████████▎ | 6764/14940 [01:27<01:39, 82.15patch/s]
45%|██████████████████████████████████████████████████████████████████████████▎ | 6773/14940 [01:27<01:38, 82.58patch/s]
45%|██████████████████████████████████████████████████████████████████████████▍ | 6782/14940 [01:27<01:40, 81.18patch/s]
45%|██████████████████████████████████████████████████████████████████████████▌ | 6791/14940 [01:27<01:40, 81.35patch/s]
46%|██████████████████████████████████████████████████████████████████████████▋ | 6800/14940 [01:27<01:40, 80.72patch/s]
46%|██████████████████████████████████████████████████████████████████████████▋ | 6809/14940 [01:27<01:39, 81.46patch/s]
46%|██████████████████████████████████████████████████████████████████████████▊ | 6818/14940 [01:27<01:39, 81.71patch/s]
46%|██████████████████████████████████████████████████████████████████████████▉ | 6827/14940 [01:28<01:38, 82.27patch/s]
46%|███████████████████████████████████████████████████████████████████████████ | 6836/14940 [01:28<01:38, 81.92patch/s]
46%|███████████████████████████████████████████████████████████████████████████▏ | 6845/14940 [01:28<01:39, 81.08patch/s]
46%|███████████████████████████████████████████████████████████████████████████▏ | 6854/14940 [01:28<01:38, 82.30patch/s]
46%|███████████████████████████████████████████████████████████████████████████▎ | 6863/14940 [01:28<01:40, 80.02patch/s]
46%|███████████████████████████████████████████████████████████████████████████▍ | 6872/14940 [01:28<01:45, 76.68patch/s]
46%|███████████████████████████████████████████████████████████████████████████▌ | 6880/14940 [01:28<01:49, 73.84patch/s]
46%|███████████████████████████████████████████████████████████████████████████▌ | 6888/14940 [01:28<01:48, 74.13patch/s]
46%|███████████████████████████████████████████████████████████████████████████▋ | 6896/14940 [01:28<01:46, 75.66patch/s]
46%|███████████████████████████████████████████████████████████████████████████▊ | 6905/14940 [01:29<01:43, 77.34patch/s]
46%|███████████████████████████████████████████████████████████████████████████▉ | 6913/14940 [01:29<01:43, 77.18patch/s]
46%|███████████████████████████████████████████████████████████████████████████▉ | 6921/14940 [01:29<01:50, 72.34patch/s]
46%|████████████████████████████████████████████████████████████████████████████ | 6929/14940 [01:29<01:49, 73.03patch/s]
46%|████████████████████████████████████████████████████████████████████████████▏ | 6937/14940 [01:29<01:47, 74.78patch/s]
46%|████████████████████████████████████████████████████████████████████████████▏ | 6945/14940 [01:29<01:55, 68.96patch/s]
47%|████████████████████████████████████████████████████████████████████████████▎ | 6953/14940 [01:29<01:51, 71.38patch/s]
47%|████████████████████████████████████████████████████████████████████████████▍ | 6961/14940 [01:29<01:49, 72.63patch/s]
47%|████████████████████████████████████████████████████████████████████████████▌ | 6970/14940 [01:29<01:45, 75.33patch/s]
47%|████████████████████████████████████████████████████████████████████████████▌ | 6978/14940 [01:30<01:50, 71.91patch/s]
47%|████████████████████████████████████████████████████████████████████████████▋ | 6986/14940 [01:30<01:57, 67.73patch/s]
47%|████████████████████████████████████████████████████████████████████████████▊ | 6994/14940 [01:30<01:54, 69.39patch/s]
47%|████████████████████████████████████████████████████████████████████████████▊ | 7002/14940 [01:30<01:51, 71.11patch/s]
47%|████████████████████████████████████████████████████████████████████████████▉ | 7010/14940 [01:30<01:51, 71.43patch/s]
47%|█████████████████████████████████████████████████████████████████████████████ | 7018/14940 [01:30<01:50, 71.38patch/s]
47%|█████████████████████████████████████████████████████████████████████████████▏ | 7026/14940 [01:30<01:51, 71.28patch/s]
47%|█████████████████████████████████████████████████████████████████████████████▏ | 7034/14940 [01:30<01:52, 70.39patch/s]
47%|█████████████████████████████████████████████████████████████████████████████▎ | 7042/14940 [01:30<01:51, 70.79patch/s]
47%|█████████████████████████████████████████████████████████████████████████████▍ | 7050/14940 [01:31<01:50, 71.49patch/s]
47%|█████████████████████████████████████████████████████████████████████████████▍ | 7058/14940 [01:31<01:49, 72.24patch/s]
47%|█████████████████████████████████████████████████████████████████████████████▌ | 7067/14940 [01:31<01:46, 74.20patch/s]
47%|█████████████████████████████████████████████████████████████████████████████▋ | 7075/14940 [01:31<01:46, 74.02patch/s]
47%|█████████████████████████████████████████████████████████████████████████████▊ | 7084/14940 [01:31<01:43, 76.00patch/s]
47%|█████████████████████████████████████████████████████████████████████████████▊ | 7092/14940 [01:31<01:42, 76.73patch/s]
48%|█████████████████████████████████████████████████████████████████████████████▉ | 7100/14940 [01:31<01:51, 70.17patch/s]
48%|██████████████████████████████████████████████████████████████████████████████ | 7108/14940 [01:31<01:49, 71.26patch/s]
48%|██████████████████████████████████████████████████████████████████████████████ | 7116/14940 [01:31<01:50, 70.90patch/s]
48%|██████████████████████████████████████████████████████████████████████████████▏ | 7125/14940 [01:32<01:44, 74.86patch/s]
48%|██████████████████████████████████████████████████████████████████████████████▎ | 7133/14940 [01:32<01:43, 75.36patch/s]
48%|██████████████████████████████████████████████████████████████████████████████▍ | 7141/14940 [01:32<01:44, 74.39patch/s]
48%|██████████████████████████████████████████████████████████████████████████████▍ | 7149/14940 [01:32<01:43, 75.63patch/s]
48%|██████████████████████████████████████████████████████████████████████████████▌ | 7157/14940 [01:32<01:41, 76.65patch/s]
48%|██████████████████████████████████████████████████████████████████████████████▋ | 7166/14940 [01:32<01:45, 73.54patch/s]
48%|██████████████████████████████████████████████████████████████████████████████▊ | 7175/14940 [01:32<01:42, 75.86patch/s]
48%|██████████████████████████████████████████████████████████████████████████████▊ | 7184/14940 [01:32<01:39, 77.60patch/s]
48%|██████████████████████████████████████████████████████████████████████████████▉ | 7193/14940 [01:32<01:39, 77.60patch/s]
48%|███████████████████████████████████████████████████████████████████████████████ | 7201/14940 [01:33<01:40, 77.30patch/s]
48%|███████████████████████████████████████████████████████████████████████████████▏ | 7209/14940 [01:33<01:39, 77.92patch/s]
48%|███████████████████████████████████████████████████████████████████████████████▏ | 7218/14940 [01:33<01:37, 79.43patch/s]
48%|███████████████████████████████████████████████████████████████████████████████▎ | 7227/14940 [01:33<01:35, 80.48patch/s]
48%|███████████████████████████████████████████████████████████████████████████████▍ | 7236/14940 [01:33<01:37, 78.74patch/s]
48%|███████████████████████████████████████████████████████████████████████████████▌ | 7245/14940 [01:33<01:35, 80.40patch/s]
49%|███████████████████████████████████████████████████████████████████████████████▋ | 7254/14940 [01:33<01:40, 76.85patch/s]
49%|███████████████████████████████████████████████████████████████████████████████▋ | 7262/14940 [01:33<01:41, 75.90patch/s]
49%|███████████████████████████████████████████████████████████████████████████████▊ | 7270/14940 [01:34<01:56, 65.87patch/s]
49%|███████████████████████████████████████████████████████████████████████████████▉ | 7277/14940 [01:34<01:57, 65.17patch/s]
49%|███████████████████████████████████████████████████████████████████████████████▉ | 7284/14940 [01:34<01:57, 64.97patch/s]
49%|████████████████████████████████████████████████████████████████████████████████ | 7291/14940 [01:34<01:58, 64.52patch/s]
49%|████████████████████████████████████████████████████████████████████████████████▏ | 7300/14940 [01:34<01:50, 69.07patch/s]
49%|████████████████████████████████████████████████████████████████████████████████▏ | 7308/14940 [01:34<01:46, 71.46patch/s]
49%|████████████████████████████████████████████████████████████████████████████████▎ | 7316/14940 [01:34<01:43, 73.35patch/s]
49%|████████████████████████████████████████████████████████████████████████████████▍ | 7324/14940 [01:34<01:42, 74.19patch/s]
49%|████████████████████████████████████████████████████████████████████████████████▍ | 7332/14940 [01:34<01:40, 75.52patch/s]
49%|████████████████████████████████████████████████████████████████████████████████▌ | 7340/14940 [01:34<01:39, 76.56patch/s]
49%|████████████████████████████████████████████████████████████████████████████████▋ | 7348/14940 [01:35<01:38, 77.35patch/s]
49%|████████████████████████████████████████████████████████████████████████████████▋ | 7356/14940 [01:35<01:38, 76.90patch/s]
49%|████████████████████████████████████████████████████████████████████████████████▊ | 7365/14940 [01:35<01:36, 78.43patch/s]
49%|████████████████████████████████████████████████████████████████████████████████▉ | 7374/14940 [01:35<01:35, 79.35patch/s]
49%|█████████████████████████████████████████████████████████████████████████████████ | 7383/14940 [01:35<01:33, 80.42patch/s]
49%|█████████████████████████████████████████████████████████████████████████████████▏ | 7392/14940 [01:35<01:40, 75.02patch/s]
50%|█████████████████████████████████████████████████████████████████████████████████▏ | 7400/14940 [01:35<01:43, 72.73patch/s]
50%|█████████████████████████████████████████████████████████████████████████████████▎ | 7408/14940 [01:35<01:44, 71.77patch/s]
50%|█████████████████████████████████████████████████████████████████████████████████▍ | 7417/14940 [01:35<01:41, 74.36patch/s]
50%|█████████████████████████████████████████████████████████████████████████████████▌ | 7425/14940 [01:36<01:39, 75.74patch/s]
50%|█████████████████████████████████████████████████████████████████████████████████▌ | 7433/14940 [01:36<01:44, 72.05patch/s]
50%|█████████████████████████████████████████████████████████████████████████████████▋ | 7441/14940 [01:36<01:53, 65.95patch/s]
50%|█████████████████████████████████████████████████████████████████████████████████▊ | 7448/14940 [01:36<01:55, 64.73patch/s]
50%|█████████████████████████████████████████████████████████████████████████████████▊ | 7456/14940 [01:36<01:52, 66.73patch/s]
50%|█████████████████████████████████████████████████████████████████████████████████▉ | 7464/14940 [01:36<01:49, 68.51patch/s]
50%|██████████████████████████████████████████████████████████████████████████████████ | 7471/14940 [01:36<01:53, 65.91patch/s]
50%|██████████████████████████████████████████████████████████████████████████████████ | 7479/14940 [01:36<01:48, 69.01patch/s]
50%|██████████████████████████████████████████████████████████████████████████████████▏ | 7488/14940 [01:37<01:42, 72.69patch/s]
50%|██████████████████████████████████████████████████████████████████████████████████▎ | 7497/14940 [01:37<01:39, 75.12patch/s]
50%|██████████████████████████████████████████████████████████████████████████████████▍ | 7506/14940 [01:37<01:36, 77.09patch/s]
50%|██████████████████████████████████████████████████████████████████████████████████▍ | 7514/14940 [01:37<01:36, 77.19patch/s]
50%|██████████████████████████████████████████████████████████████████████████████████▌ | 7522/14940 [01:37<01:41, 72.78patch/s]
50%|██████████████████████████████████████████████████████████████████████████████████▋ | 7530/14940 [01:37<01:46, 69.74patch/s]
50%|██████████████████████████████████████████████████████████████████████████████████▋ | 7538/14940 [01:37<01:47, 69.15patch/s]
51%|██████████████████████████████████████████████████████████████████████████████████▊ | 7546/14940 [01:37<01:43, 71.12patch/s]
51%|██████████████████████████████████████████████████████████████████████████████████▉ | 7554/14940 [01:37<01:45, 69.74patch/s]
51%|███████████████████████████████████████████████████████████████████████████████████ | 7562/14940 [01:38<01:50, 66.51patch/s]
51%|███████████████████████████████████████████████████████████████████████████████████ | 7570/14940 [01:38<01:46, 69.03patch/s]
51%|███████████████████████████████████████████████████████████████████████████████████▏ | 7578/14940 [01:38<01:44, 70.44patch/s]
51%|███████████████████████████████████████████████████████████████████████████████████▎ | 7587/14940 [01:38<01:39, 73.71patch/s]
51%|███████████████████████████████████████████████████████████████████████████████████▎ | 7595/14940 [01:38<01:38, 74.70patch/s]
51%|███████████████████████████████████████████████████████████████████████████████████▍ | 7604/14940 [01:38<01:35, 77.06patch/s]
51%|███████████████████████████████████████████████████████████████████████████████████▌ | 7612/14940 [01:38<01:36, 76.01patch/s]
51%|███████████████████████████████████████████████████████████████████████████████████▋ | 7620/14940 [01:38<01:37, 74.76patch/s]
51%|███████████████████████████████████████████████████████████████████████████████████▋ | 7629/14940 [01:38<01:35, 76.83patch/s]
51%|███████████████████████████████████████████████████████████████████████████████████▊ | 7638/14940 [01:39<01:33, 78.39patch/s]
51%|███████████████████████████████████████████████████████████████████████████████████▉ | 7646/14940 [01:39<01:35, 76.04patch/s]
51%|████████████████████████████████████████████████████████████████████████████████████ | 7654/14940 [01:39<01:34, 77.05patch/s]
51%|████████████████████████████████████████████████████████████████████████████████████ | 7662/14940 [01:39<01:35, 75.94patch/s]
51%|████████████████████████████████████████████████████████████████████████████████████▏ | 7670/14940 [01:39<01:34, 76.68patch/s]
51%|████████████████████████████████████████████████████████████████████████████████████▎ | 7679/14940 [01:39<01:32, 78.21patch/s]
51%|████████████████████████████████████████████████████████████████████████████████████▍ | 7688/14940 [01:39<01:31, 79.34patch/s]
52%|████████████████████████████████████████████████████████████████████████████████████▍ | 7696/14940 [01:39<01:32, 78.43patch/s]
52%|████████████████████████████████████████████████████████████████████████████████████▌ | 7704/14940 [01:39<01:34, 76.57patch/s]
52%|████████████████████████████████████████████████████████████████████████████████████▋ | 7712/14940 [01:40<01:34, 76.80patch/s]
52%|████████████████████████████████████████████████████████████████████████████████████▋ | 7720/14940 [01:40<01:35, 75.89patch/s]
52%|████████████████████████████████████████████████████████████████████████████████████▊ | 7728/14940 [01:40<01:37, 74.21patch/s]
52%|████████████████████████████████████████████████████████████████████████████████████▉ | 7736/14940 [01:40<01:35, 75.30patch/s]
52%|█████████████████████████████████████████████████████████████████████████████████████ | 7745/14940 [01:40<01:32, 78.18patch/s]
52%|█████████████████████████████████████████████████████████████████████████████████████ | 7754/14940 [01:40<01:31, 78.73patch/s]
52%|█████████████████████████████████████████████████████████████████████████████████████▏ | 7762/14940 [01:40<01:33, 77.01patch/s]
52%|█████████████████████████████████████████████████████████████████████████████████████▎ | 7770/14940 [01:40<01:33, 76.66patch/s]
52%|█████████████████████████████████████████████████████████████████████████████████████▍ | 7778/14940 [01:40<01:33, 76.24patch/s]
52%|█████████████████████████████████████████████████████████████████████████████████████▍ | 7786/14940 [01:40<01:35, 74.55patch/s]
52%|█████████████████████████████████████████████████████████████████████████████████████▌ | 7794/14940 [01:41<01:36, 74.06patch/s]
52%|█████████████████████████████████████████████████████████████████████████████████████▋ | 7802/14940 [01:41<01:37, 73.16patch/s]
52%|█████████████████████████████████████████████████████████████████████████████████████▋ | 7810/14940 [01:41<01:41, 70.52patch/s]
52%|█████████████████████████████████████████████████████████████████████████████████████▊ | 7818/14940 [01:41<01:39, 71.55patch/s]
52%|█████████████████████████████████████████████████████████████████████████████████████▉ | 7826/14940 [01:41<01:38, 72.00patch/s]
52%|█████████████████████████████████████████████████████████████████████████████████████▉ | 7834/14940 [01:41<01:36, 73.27patch/s]
52%|██████████████████████████████████████████████████████████████████████████████████████ | 7842/14940 [01:41<01:37, 73.14patch/s]
53%|██████████████████████████████████████████████████████████████████████████████████████▏ | 7850/14940 [01:41<01:36, 73.55patch/s]
53%|██████████████████████████████████████████████████████████████████████████████████████▎ | 7858/14940 [01:41<01:37, 72.76patch/s]
53%|██████████████████████████████████████████████████████████████████████████████████████▎ | 7866/14940 [01:42<01:37, 72.33patch/s]
53%|██████████████████████████████████████████████████████████████████████████████████████▍ | 7874/14940 [01:42<01:51, 63.10patch/s]
53%|██████████████████████████████████████████████████████████████████████████████████████▌ | 7882/14940 [01:42<01:47, 65.42patch/s]
53%|██████████████████████████████████████████████████████████████████████████████████████▌ | 7890/14940 [01:42<01:43, 67.81patch/s]
53%|██████████████████████████████████████████████████████████████████████████████████████▋ | 7899/14940 [01:42<01:37, 72.36patch/s]
53%|██████████████████████████████████████████████████████████████████████████████████████▊ | 7907/14940 [01:42<01:45, 66.82patch/s]
53%|██████████████████████████████████████████████████████████████████████████████████████▊ | 7914/14940 [01:42<01:49, 64.01patch/s]
53%|██████████████████████████████████████████████████████████████████████████████████████▉ | 7921/14940 [01:42<01:50, 63.49patch/s]
53%|███████████████████████████████████████████████████████████████████████████████████████ | 7929/14940 [01:43<01:46, 65.97patch/s]
53%|███████████████████████████████████████████████████████████████████████████████████████▏ | 7937/14940 [01:43<01:41, 68.86patch/s]
53%|███████████████████████████████████████████████████████████████████████████████████████▏ | 7946/14940 [01:43<01:35, 72.94patch/s]
53%|███████████████████████████████████████████████████████████████████████████████████████▎ | 7955/14940 [01:43<01:32, 75.83patch/s]
53%|███████████████████████████████████████████████████████████████████████████████████████▍ | 7963/14940 [01:43<01:39, 69.93patch/s]
53%|███████████████████████████████████████████████████████████████████████████████████████▍ | 7971/14940 [01:43<01:44, 66.45patch/s]
53%|███████████████████████████████████████████████████████████████████████████████████████▌ | 7978/14940 [01:43<01:45, 66.05patch/s]
53%|███████████████████████████████████████████████████████████████████████████████████████▋ | 7985/14940 [01:43<01:45, 66.23patch/s]
54%|███████████████████████████████████████████████████████████████████████████████████████▋ | 7993/14940 [01:43<01:40, 69.39patch/s]
54%|███████████████████████████████████████████████████████████████████████████████████████▊ | 8001/14940 [01:44<01:38, 70.33patch/s]
54%|███████████████████████████████████████████████████████████████████████████████████████▉ | 8009/14940 [01:44<01:35, 72.81patch/s]
54%|████████████████████████████████████████████████████████████████████████████████████████ | 8017/14940 [01:44<01:36, 71.89patch/s]
54%|████████████████████████████████████████████████████████████████████████████████████████ | 8026/14940 [01:44<01:31, 75.22patch/s]
54%|████████████████████████████████████████████████████████████████████████████████████████▏ | 8035/14940 [01:44<01:29, 77.31patch/s]
54%|████████████████████████████████████████████████████████████████████████████████████████▎ | 8043/14940 [01:44<01:28, 77.64patch/s]
54%|████████████████████████████████████████████████████████████████████████████████████████▍ | 8051/14940 [01:44<01:31, 75.69patch/s]
54%|████████████████████████████████████████████████████████████████████████████████████████▍ | 8059/14940 [01:44<01:40, 68.42patch/s]
54%|████████████████████████████████████████████████████████████████████████████████████████▌ | 8066/14940 [01:44<01:40, 68.54patch/s]
54%|████████████████████████████████████████████████████████████████████████████████████████▋ | 8074/14940 [01:45<01:36, 71.12patch/s]
54%|████████████████████████████████████████████████████████████████████████████████████████▋ | 8082/14940 [01:45<01:35, 71.81patch/s]
54%|████████████████████████████████████████████████████████████████████████████████████████▊ | 8090/14940 [01:45<01:37, 70.08patch/s]
54%|████████████████████████████████████████████████████████████████████████████████████████▉ | 8098/14940 [01:45<01:37, 70.14patch/s]
54%|████████████████████████████████████████████████████████████████████████████████████████▉ | 8106/14940 [01:45<01:40, 68.27patch/s]
54%|█████████████████████████████████████████████████████████████████████████████████████████ | 8114/14940 [01:45<01:35, 71.31patch/s]
54%|█████████████████████████████████████████████████████████████████████████████████████████▏ | 8122/14940 [01:45<01:36, 70.89patch/s]
54%|█████████████████████████████████████████████████████████████████████████████████████████▏ | 8130/14940 [01:45<01:38, 68.87patch/s]
54%|█████████████████████████████████████████████████████████████████████████████████████████▎ | 8138/14940 [01:45<01:35, 71.13patch/s]
55%|█████████████████████████████████████████████████████████████████████████████████████████▍ | 8146/14940 [01:46<01:33, 72.73patch/s]
55%|█████████████████████████████████████████████████████████████████████████████████████████▌ | 8154/14940 [01:46<01:36, 70.52patch/s]
55%|█████████████████████████████████████████████████████████████████████████████████████████▌ | 8162/14940 [01:46<01:38, 69.16patch/s]
55%|█████████████████████████████████████████████████████████████████████████████████████████▋ | 8169/14940 [01:46<01:38, 68.48patch/s]
55%|█████████████████████████████████████████████████████████████████████████████████████████▋ | 8176/14940 [01:46<01:40, 67.37patch/s]
55%|█████████████████████████████████████████████████████████████████████████████████████████▊ | 8184/14940 [01:46<01:38, 68.74patch/s]
55%|█████████████████████████████████████████████████████████████████████████████████████████▉ | 8192/14940 [01:46<01:35, 70.61patch/s]
55%|██████████████████████████████████████████████████████████████████████████████████████████ | 8200/14940 [01:46<01:36, 70.21patch/s]
55%|██████████████████████████████████████████████████████████████████████████████████████████ | 8208/14940 [01:47<01:35, 70.58patch/s]
55%|██████████████████████████████████████████████████████████████████████████████████████████▏ | 8216/14940 [01:47<01:37, 68.81patch/s]
55%|██████████████████████████████████████████████████████████████████████████████████████████▎ | 8223/14940 [01:47<01:40, 66.81patch/s]
55%|██████████████████████████████████████████████████████████████████████████████████████████▎ | 8230/14940 [01:47<01:42, 65.53patch/s]
55%|██████████████████████████████████████████████████████████████████████████████████████████▍ | 8239/14940 [01:47<01:34, 70.81patch/s]
55%|██████████████████████████████████████████████████████████████████████████████████████████▌ | 8248/14940 [01:47<01:29, 74.69patch/s]
55%|██████████████████████████████████████████████████████████████████████████████████████████▋ | 8257/14940 [01:47<01:26, 77.45patch/s]
55%|██████████████████████████████████████████████████████████████████████████████████████████▋ | 8265/14940 [01:47<01:25, 78.09patch/s]
55%|██████████████████████████████████████████████████████████████████████████████████████████▊ | 8274/14940 [01:47<01:24, 79.32patch/s]
55%|██████████████████████████████████████████████████████████████████████████████████████████▉ | 8283/14940 [01:47<01:23, 79.70patch/s]
56%|███████████████████████████████████████████████████████████████████████████████████████████ | 8292/14940 [01:48<01:22, 80.17patch/s]
56%|███████████████████████████████████████████████████████████████████████████████████████████ | 8301/14940 [01:48<01:21, 81.33patch/s]
56%|███████████████████████████████████████████████████████████████████████████████████████████▏ | 8310/14940 [01:48<01:20, 82.03patch/s]
56%|███████████████████████████████████████████████████████████████████████████████████████████▎ | 8319/14940 [01:48<01:20, 82.28patch/s]
56%|███████████████████████████████████████████████████████████████████████████████████████████▍ | 8328/14940 [01:48<01:20, 82.38patch/s]
56%|███████████████████████████████████████████████████████████████████████████████████████████▌ | 8337/14940 [01:48<01:20, 82.32patch/s]
56%|███████████████████████████████████████████████████████████████████████████████████████████▌ | 8346/14940 [01:48<01:22, 79.53patch/s]
56%|███████████████████████████████████████████████████████████████████████████████████████████▋ | 8354/14940 [01:48<01:25, 77.45patch/s]
56%|███████████████████████████████████████████████████████████████████████████████████████████▊ | 8363/14940 [01:48<01:23, 78.68patch/s]
56%|███████████████████████████████████████████████████████████████████████████████████████████▉ | 8372/14940 [01:49<01:22, 79.55patch/s]
56%|███████████████████████████████████████████████████████████████████████████████████████████▉ | 8380/14940 [01:49<01:23, 78.98patch/s]
56%|████████████████████████████████████████████████████████████████████████████████████████████ | 8388/14940 [01:49<01:23, 78.03patch/s]
56%|████████████████████████████████████████████████████████████████████████████████████████████▏ | 8397/14940 [01:49<01:23, 78.64patch/s]
56%|████████████████████████████████████████████████████████████████████████████████████████████▎ | 8405/14940 [01:49<01:25, 76.77patch/s]
56%|████████████████████████████████████████████████████████████████████████████████████████████▎ | 8413/14940 [01:49<01:27, 74.66patch/s]
56%|████████████████████████████████████████████████████████████████████████████████████████████▍ | 8421/14940 [01:49<01:25, 75.91patch/s]
56%|████████████████████████████████████████████████████████████████████████████████████████████▌ | 8430/14940 [01:49<01:24, 76.95patch/s]
56%|████████████████████████████████████████████████████████████████████████████████████████████▋ | 8438/14940 [01:49<01:28, 73.62patch/s]
57%|████████████████████████████████████████████████████████████████████████████████████████████▋ | 8446/14940 [01:50<01:28, 73.63patch/s]
57%|████████████████████████████████████████████████████████████████████████████████████████████▊ | 8454/14940 [01:50<01:36, 67.10patch/s]
57%|████████████████████████████████████████████████████████████████████████████████████████████▉ | 8462/14940 [01:50<01:34, 68.49patch/s]
57%|████████████████████████████████████████████████████████████████████████████████████████████▉ | 8470/14940 [01:50<01:32, 69.78patch/s]
57%|█████████████████████████████████████████████████████████████████████████████████████████████ | 8479/14940 [01:50<01:29, 72.35patch/s]
57%|█████████████████████████████████████████████████████████████████████████████████████████████▏ | 8487/14940 [01:50<01:27, 74.05patch/s]
57%|█████████████████████████████████████████████████████████████████████████████████████████████▎ | 8495/14940 [01:50<01:26, 74.35patch/s]
57%|█████████████████████████████████████████████████████████████████████████████████████████████▎ | 8504/14940 [01:50<01:24, 76.32patch/s]
57%|█████████████████████████████████████████████████████████████████████████████████████████████▍ | 8512/14940 [01:51<01:32, 69.63patch/s]
57%|█████████████████████████████████████████████████████████████████████████████████████████████▌ | 8520/14940 [01:51<01:31, 69.94patch/s]
57%|█████████████████████████████████████████████████████████████████████████████████████████████▌ | 8528/14940 [01:51<01:30, 71.21patch/s]
57%|█████████████████████████████████████████████████████████████████████████████████████████████▋ | 8536/14940 [01:51<01:27, 73.55patch/s]
57%|█████████████████████████████████████████████████████████████████████████████████████████████▊ | 8545/14940 [01:51<01:24, 76.06patch/s]
57%|█████████████████████████████████████████████████████████████████████████████████████████████▉ | 8554/14940 [01:51<01:22, 77.54patch/s]
57%|█████████████████████████████████████████████████████████████████████████████████████████████▉ | 8563/14940 [01:51<01:21, 78.49patch/s]
57%|██████████████████████████████████████████████████████████████████████████████████████████████ | 8572/14940 [01:51<01:20, 79.19patch/s]
57%|██████████████████████████████████████████████████████████████████████████████████████████████▏ | 8580/14940 [01:51<01:20, 79.37patch/s]
57%|██████████████████████████████████████████████████████████████████████████████████████████████▎ | 8588/14940 [01:51<01:20, 79.17patch/s]
58%|██████████████████████████████████████████████████████████████████████████████████████████████▎ | 8596/14940 [01:52<01:22, 77.16patch/s]
58%|██████████████████████████████████████████████████████████████████████████████████████████████▍ | 8604/14940 [01:52<01:21, 77.63patch/s]
58%|██████████████████████████████████████████████████████████████████████████████████████████████▌ | 8612/14940 [01:52<01:21, 78.00patch/s]
58%|██████████████████████████████████████████████████████████████████████████████████████████████▌ | 8620/14940 [01:52<01:32, 68.19patch/s]
58%|██████████████████████████████████████████████████████████████████████████████████████████████▋ | 8628/14940 [01:52<01:33, 67.51patch/s]
58%|██████████████████████████████████████████████████████████████████████████████████████████████▊ | 8636/14940 [01:52<01:29, 70.14patch/s]
58%|██████████████████████████████████████████████████████████████████████████████████████████████▉ | 8644/14940 [01:52<01:27, 72.36patch/s]
58%|██████████████████████████████████████████████████████████████████████████████████████████████▉ | 8652/14940 [01:52<01:25, 73.88patch/s]
58%|███████████████████████████████████████████████████████████████████████████████████████████████ | 8660/14940 [01:52<01:23, 75.06patch/s]
58%|███████████████████████████████████████████████████████████████████████████████████████████████▏ | 8668/14940 [01:53<01:22, 75.76patch/s]
58%|███████████████████████████████████████████████████████████████████████████████████████████████▏ | 8677/14940 [01:53<01:20, 77.99patch/s]
58%|███████████████████████████████████████████████████████████████████████████████████████████████▎ | 8686/14940 [01:53<01:18, 79.22patch/s]
58%|███████████████████████████████████████████████████████████████████████████████████████████████▍ | 8694/14940 [01:53<01:20, 77.12patch/s]
58%|███████████████████████████████████████████████████████████████████████████████████████████████▌ | 8702/14940 [01:53<01:25, 72.87patch/s]
58%|███████████████████████████████████████████████████████████████████████████████████████████████▌ | 8710/14940 [01:53<01:25, 73.16patch/s]
58%|███████████████████████████████████████████████████████████████████████████████████████████████▋ | 8718/14940 [01:53<01:25, 72.83patch/s]
58%|███████████████████████████████████████████████████████████████████████████████████████████████▊ | 8726/14940 [01:53<01:25, 72.81patch/s]
58%|███████████████████████████████████████████████████████████████████████████████████████████████▉ | 8734/14940 [01:53<01:24, 73.66patch/s]
59%|███████████████████████████████████████████████████████████████████████████████████████████████▉ | 8742/14940 [01:54<01:22, 74.84patch/s]
59%|████████████████████████████████████████████████████████████████████████████████████████████████ | 8751/14940 [01:54<01:20, 77.00patch/s]
59%|████████████████████████████████████████████████████████████████████████████████████████████████▏ | 8760/14940 [01:54<01:18, 78.50patch/s]
59%|████████████████████████████████████████████████████████████████████████████████████████████████▎ | 8769/14940 [01:54<01:17, 79.32patch/s]
59%|████████████████████████████████████████████████████████████████████████████████████████████████▎ | 8777/14940 [01:54<01:17, 79.39patch/s]
59%|████████████████████████████████████████████████████████████████████████████████████████████████▍ | 8785/14940 [01:54<01:19, 77.38patch/s]
59%|████████████████████████████████████████████████████████████████████████████████████████████████▌ | 8793/14940 [01:54<01:19, 77.06patch/s]
59%|████████████████████████████████████████████████████████████████████████████████████████████████▌ | 8802/14940 [01:54<01:18, 78.11patch/s]
59%|████████████████████████████████████████████████████████████████████████████████████████████████▋ | 8810/14940 [01:54<01:23, 73.26patch/s]
59%|████████████████████████████████████████████████████████████████████████████████████████████████▊ | 8818/14940 [01:55<01:24, 72.41patch/s]
59%|████████████████████████████████████████████████████████████████████████████████████████████████▉ | 8826/14940 [01:55<01:24, 72.64patch/s]
59%|████████████████████████████████████████████████████████████████████████████████████████████████▉ | 8834/14940 [01:55<01:23, 73.46patch/s]
59%|█████████████████████████████████████████████████████████████████████████████████████████████████ | 8843/14940 [01:55<01:19, 76.39patch/s]
59%|█████████████████████████████████████████████████████████████████████████████████████████████████▏ | 8852/14940 [01:55<01:17, 78.48patch/s]
59%|█████████████████████████████████████████████████████████████████████████████████████████████████▎ | 8861/14940 [01:55<01:16, 79.41patch/s]
59%|█████████████████████████████████████████████████████████████████████████████████████████████████▎ | 8869/14940 [01:55<01:21, 74.85patch/s]
59%|█████████████████████████████████████████████████████████████████████████████████████████████████▍ | 8877/14940 [01:55<01:21, 74.45patch/s]
59%|█████████████████████████████████████████████████████████████████████████████████████████████████▌ | 8886/14940 [01:55<01:19, 76.02patch/s]
60%|█████████████████████████████████████████████████████████████████████████████████████████████████▋ | 8894/14940 [01:56<01:23, 72.61patch/s]
60%|█████████████████████████████████████████████████████████████████████████████████████████████████▋ | 8902/14940 [01:56<01:24, 71.56patch/s]
60%|█████████████████████████████████████████████████████████████████████████████████████████████████▊ | 8910/14940 [01:56<01:22, 73.50patch/s]
60%|█████████████████████████████████████████████████████████████████████████████████████████████████▉ | 8919/14940 [01:56<01:19, 75.81patch/s]
60%|██████████████████████████████████████████████████████████████████████████████████████████████████ | 8928/14940 [01:56<01:17, 77.79patch/s]
60%|██████████████████████████████████████████████████████████████████████████████████████████████████ | 8937/14940 [01:56<01:15, 79.05patch/s]
60%|██████████████████████████████████████████████████████████████████████████████████████████████████▏ | 8945/14940 [01:56<01:18, 76.78patch/s]
60%|██████████████████████████████████████████████████████████████████████████████████████████████████▎ | 8953/14940 [01:56<01:19, 75.46patch/s]
60%|██████████████████████████████████████████████████████████████████████████████████████████████████▎ | 8961/14940 [01:56<01:18, 76.05patch/s]
60%|██████████████████████████████████████████████████████████████████████████████████████████████████▍ | 8970/14940 [01:57<01:16, 78.48patch/s]
60%|██████████████████████████████████████████████████████████████████████████████████████████████████▌ | 8979/14940 [01:57<01:14, 79.93patch/s]
60%|██████████████████████████████████████████████████████████████████████████████████████████████████▋ | 8988/14940 [01:57<01:13, 80.82patch/s]
60%|██████████████████████████████████████████████████████████████████████████████████████████████████▊ | 8997/14940 [01:57<01:13, 80.71patch/s]
60%|██████████████████████████████████████████████████████████████████████████████████████████████████▊ | 9006/14940 [01:57<01:12, 81.53patch/s]
60%|██████████████████████████████████████████████████████████████████████████████████████████████████▉ | 9015/14940 [01:57<01:12, 81.87patch/s]
60%|███████████████████████████████████████████████████████████████████████████████████████████████████ | 9024/14940 [01:57<01:13, 80.50patch/s]
60%|███████████████████████████████████████████████████████████████████████████████████████████████████▏ | 9033/14940 [01:57<01:14, 79.29patch/s]
61%|███████████████████████████████████████████████████████████████████████████████████████████████████▏ | 9041/14940 [01:57<01:15, 78.37patch/s]
61%|███████████████████████████████████████████████████████████████████████████████████████████████████▎ | 9049/14940 [01:58<01:14, 78.72patch/s]
61%|███████████████████████████████████████████████████████████████████████████████████████████████████▍ | 9058/14940 [01:58<01:13, 79.73patch/s]
61%|███████████████████████████████████████████████████████████████████████████████████████████████████▌ | 9066/14940 [01:58<01:13, 79.50patch/s]
61%|███████████████████████████████████████████████████████████████████████████████████████████████████▌ | 9074/14940 [01:58<01:14, 79.15patch/s]
61%|███████████████████████████████████████████████████████████████████████████████████████████████████▋ | 9082/14940 [01:58<01:15, 77.34patch/s]
61%|███████████████████████████████████████████████████████████████████████████████████████████████████▊ | 9090/14940 [01:58<01:16, 76.88patch/s]
61%|███████████████████████████████████████████████████████████████████████████████████████████████████▊ | 9098/14940 [01:58<01:15, 77.75patch/s]
61%|████████████████████████████████████████████████████████████████████████████████████████████████████ | 9113/14940 [01:58<00:59, 97.90patch/s]
61%|███████████████████████████████████████████████████████████████████████████████████████████████████▌ | 9130/14940 [01:58<00:49, 117.04patch/s]
61%|███████████████████████████████████████████████████████████████████████████████████████████████████▊ | 9147/14940 [01:58<00:44, 130.62patch/s]
61%|███████████████████████████████████████████████████████████████████████████████████████████████████▉ | 9163/14940 [01:59<00:41, 137.97patch/s]
61%|████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 9179/14940 [01:59<00:40, 143.26patch/s]
62%|████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 9195/14940 [01:59<00:38, 147.79patch/s]
62%|████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 9211/14940 [01:59<00:37, 151.22patch/s]
62%|████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 9228/14940 [01:59<00:37, 154.11patch/s]
62%|████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 9244/14940 [01:59<00:36, 155.50patch/s]
62%|█████████████████████████████████████████████████████████████████████████████████████████████████████ | 9260/14940 [01:59<00:36, 155.58patch/s]
62%|█████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 9276/14940 [01:59<00:36, 156.65patch/s]
62%|█████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 9293/14940 [01:59<00:35, 157.41patch/s]
62%|█████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 9309/14940 [02:00<00:35, 157.79patch/s]
62%|█████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 9325/14940 [02:00<00:35, 157.50patch/s]
63%|█████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 9341/14940 [02:00<00:35, 157.73patch/s]
63%|██████████████████████████████████████████████████████████████████████████████████████████████████████ | 9358/14940 [02:00<00:35, 159.25patch/s]
63%|██████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 9374/14940 [02:00<00:35, 158.99patch/s]
63%|██████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 9390/14940 [02:00<00:34, 158.90patch/s]
63%|██████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 9406/14940 [02:00<00:35, 156.62patch/s]
63%|██████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 9422/14940 [02:00<00:35, 155.27patch/s]
63%|██████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 9439/14940 [02:00<00:34, 157.38patch/s]
63%|███████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 9455/14940 [02:00<00:35, 155.64patch/s]
63%|███████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 9471/14940 [02:01<00:35, 154.01patch/s]
64%|███████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 9487/14940 [02:01<00:35, 154.00patch/s]
64%|███████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 9503/14940 [02:01<00:35, 153.14patch/s]
64%|███████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 9519/14940 [02:01<00:35, 153.23patch/s]
64%|████████████████████████████████████████████████████████████████████████████████████████████████████████ | 9535/14940 [02:01<00:34, 154.90patch/s]
64%|████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 9551/14940 [02:01<00:34, 155.05patch/s]
64%|████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 9567/14940 [02:01<00:34, 154.76patch/s]
64%|████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 9583/14940 [02:01<00:34, 155.47patch/s]
64%|████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 9599/14940 [02:01<00:34, 155.33patch/s]
64%|████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 9615/14940 [02:01<00:34, 155.87patch/s]
64%|█████████████████████████████████████████████████████████████████████████████████████████████████████████ | 9631/14940 [02:02<00:33, 156.28patch/s]
65%|█████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 9647/14940 [02:02<00:33, 155.75patch/s]
65%|█████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 9663/14940 [02:02<00:33, 156.75patch/s]
65%|█████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 9679/14940 [02:02<00:33, 156.65patch/s]
65%|█████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 9695/14940 [02:02<00:33, 156.74patch/s]
65%|█████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 9711/14940 [02:02<00:33, 156.13patch/s]
65%|██████████████████████████████████████████████████████████████████████████████████████████████████████████ | 9727/14940 [02:02<00:33, 155.50patch/s]
65%|██████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 9743/14940 [02:02<00:33, 156.03patch/s]
65%|██████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 9759/14940 [02:02<00:33, 156.82patch/s]
65%|██████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 9775/14940 [02:03<00:33, 156.50patch/s]
66%|██████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 9791/14940 [02:03<00:32, 157.25patch/s]
66%|██████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 9807/14940 [02:03<00:32, 157.67patch/s]
66%|███████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 9824/14940 [02:03<00:32, 158.61patch/s]
66%|███████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 9840/14940 [02:03<00:32, 158.41patch/s]
66%|███████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 9856/14940 [02:03<00:32, 158.53patch/s]
66%|███████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 9872/14940 [02:03<00:31, 158.95patch/s]
66%|███████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 9889/14940 [02:03<00:31, 160.05patch/s]
66%|████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 9906/14940 [02:03<00:31, 159.29patch/s]
66%|████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 9923/14940 [02:03<00:31, 160.17patch/s]
67%|████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 9940/14940 [02:04<00:31, 158.50patch/s]
67%|████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 9956/14940 [02:04<00:31, 157.19patch/s]
67%|████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 9972/14940 [02:04<00:31, 157.10patch/s]
67%|████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 9988/14940 [02:04<00:31, 156.78patch/s]
67%|████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 10004/14940 [02:04<00:32, 153.67patch/s]
67%|████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 10020/14940 [02:04<00:32, 152.48patch/s]
67%|████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 10036/14940 [02:04<00:31, 154.07patch/s]
67%|████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 10052/14940 [02:04<00:31, 155.33patch/s]
67%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 10068/14940 [02:04<00:31, 156.19patch/s]
67%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 10084/14940 [02:04<00:31, 155.78patch/s]
68%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 10100/14940 [02:05<00:31, 154.29patch/s]
68%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 10116/14940 [02:05<00:31, 151.92patch/s]
68%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 10132/14940 [02:05<00:32, 146.95patch/s]
68%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 10148/14940 [02:05<00:32, 148.74patch/s]
68%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 10164/14940 [02:05<00:31, 151.81patch/s]
68%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 10180/14940 [02:05<00:30, 153.93patch/s]
68%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 10196/14940 [02:05<00:30, 155.54patch/s]
68%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 10212/14940 [02:05<00:30, 155.79patch/s]
68%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 10228/14940 [02:05<00:30, 155.69patch/s]
69%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 10244/14940 [02:06<00:30, 154.99patch/s]
69%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 10260/14940 [02:06<00:30, 152.80patch/s]
69%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 10276/14940 [02:06<00:30, 153.63patch/s]
69%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 10292/14940 [02:06<00:30, 153.35patch/s]
69%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 10308/14940 [02:06<00:30, 154.01patch/s]
69%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 10324/14940 [02:06<00:29, 155.04patch/s]
69%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 10340/14940 [02:06<00:29, 155.61patch/s]
69%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 10356/14940 [02:06<00:29, 156.51patch/s]
69%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 10372/14940 [02:06<00:29, 156.69patch/s]
70%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 10389/14940 [02:06<00:28, 158.36patch/s]
70%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 10406/14940 [02:07<00:28, 159.11patch/s]
70%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 10423/14940 [02:07<00:28, 159.58patch/s]
70%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 10440/14940 [02:07<00:28, 159.89patch/s]
70%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 10457/14940 [02:07<00:27, 160.56patch/s]
70%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 10474/14940 [02:07<00:27, 160.59patch/s]
70%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 10491/14940 [02:07<00:27, 159.42patch/s]
70%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 10507/14940 [02:07<00:27, 158.73patch/s]
70%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 10523/14940 [02:07<00:27, 158.49patch/s]
71%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 10539/14940 [02:07<00:27, 158.64patch/s]
71%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 10555/14940 [02:07<00:27, 158.91patch/s]
71%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 10572/14940 [02:08<00:27, 159.59patch/s]
71%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 10589/14940 [02:08<00:27, 159.90patch/s]
71%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 10605/14940 [02:08<00:27, 159.55patch/s]
71%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 10621/14940 [02:08<00:27, 159.29patch/s]
71%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 10637/14940 [02:08<00:27, 158.64patch/s]
71%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 10654/14940 [02:08<00:26, 159.36patch/s]
71%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 10670/14940 [02:08<00:26, 158.51patch/s]
72%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 10686/14940 [02:08<00:26, 158.91patch/s]
72%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 10703/14940 [02:08<00:26, 159.43patch/s]
72%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 10719/14940 [02:09<00:26, 158.22patch/s]
72%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 10735/14940 [02:09<00:26, 157.43patch/s]
72%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 10751/14940 [02:09<00:26, 156.81patch/s]
72%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 10767/14940 [02:09<00:26, 156.44patch/s]
72%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 10783/14940 [02:09<00:26, 156.65patch/s]
72%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 10799/14940 [02:09<00:26, 156.33patch/s]
72%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 10815/14940 [02:09<00:26, 156.43patch/s]
73%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 10832/14940 [02:09<00:26, 157.72patch/s]
73%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 10849/14940 [02:09<00:25, 158.60patch/s]
73%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 10865/14940 [02:09<00:25, 158.62patch/s]
73%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 10882/14940 [02:10<00:25, 159.28patch/s]
73%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 10899/14940 [02:10<00:25, 159.63patch/s]
73%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 10915/14940 [02:10<00:25, 158.89patch/s]
73%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 10931/14940 [02:10<00:25, 156.08patch/s]
73%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 10947/14940 [02:10<00:25, 155.93patch/s]
73%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 10964/14940 [02:10<00:25, 157.42patch/s]
73%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 10980/14940 [02:10<00:25, 157.94patch/s]
74%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 10997/14940 [02:10<00:24, 158.67patch/s]
74%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 11013/14940 [02:10<00:24, 158.91patch/s]
74%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 11029/14940 [02:10<00:24, 157.46patch/s]
74%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 11045/14940 [02:11<00:24, 157.16patch/s]
74%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 11061/14940 [02:11<00:24, 157.35patch/s]
74%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 11077/14940 [02:11<00:24, 157.05patch/s]
74%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 11094/14940 [02:11<00:24, 158.42patch/s]
74%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 11111/14940 [02:11<00:23, 160.02patch/s]
74%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 11128/14940 [02:11<00:23, 160.42patch/s]
75%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 11145/14940 [02:11<00:23, 160.07patch/s]
75%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 11162/14940 [02:11<00:23, 159.38patch/s]
75%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 11178/14940 [02:11<00:23, 159.47patch/s]
75%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 11195/14940 [02:12<00:23, 160.15patch/s]
75%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 11212/14940 [02:12<00:23, 161.20patch/s]
75%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 11229/14940 [02:12<00:22, 161.50patch/s]
75%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 11246/14940 [02:12<00:22, 161.24patch/s]
75%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 11263/14940 [02:12<00:23, 157.55patch/s]
76%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 11280/14940 [02:12<00:23, 158.56patch/s]
76%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 11297/14940 [02:12<00:22, 159.17patch/s]
76%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 11314/14940 [02:12<00:22, 159.94patch/s]
76%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 11331/14940 [02:12<00:22, 159.98patch/s]
76%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 11348/14940 [02:13<00:23, 155.72patch/s]
76%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 11365/14940 [02:13<00:22, 157.28patch/s]
76%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 11381/14940 [02:13<00:22, 156.93patch/s]
76%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 11397/14940 [02:13<00:22, 156.76patch/s]
76%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 11413/14940 [02:13<00:22, 157.68patch/s]
76%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 11429/14940 [02:13<00:22, 156.74patch/s]
77%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 11446/14940 [02:13<00:22, 158.03patch/s]
77%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 11463/14940 [02:13<00:21, 158.32patch/s]
77%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 11479/14940 [02:13<00:21, 158.63patch/s]
77%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 11496/14940 [02:13<00:21, 158.79patch/s]
77%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 11512/14940 [02:14<00:21, 157.07patch/s]
77%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 11528/14940 [02:14<00:22, 150.54patch/s]
77%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 11544/14940 [02:14<00:23, 143.29patch/s]
77%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 11559/14940 [02:14<00:23, 144.52patch/s]
77%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 11574/14940 [02:14<00:23, 142.10patch/s]
78%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 11589/14940 [02:14<00:23, 140.29patch/s]
78%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 11605/14940 [02:14<00:23, 144.67patch/s]
78%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 11620/14940 [02:14<00:22, 144.85patch/s]
78%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 11635/14940 [02:14<00:22, 143.92patch/s]
78%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 11650/14940 [02:15<00:22, 144.44patch/s]
78%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 11665/14940 [02:15<00:23, 139.54patch/s]
78%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 11680/14940 [02:15<00:23, 140.15patch/s]
78%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 11695/14940 [02:15<00:22, 141.40patch/s]
78%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 11710/14940 [02:15<00:22, 143.18patch/s]
78%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 11726/14940 [02:15<00:22, 145.77patch/s]
79%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 11741/14940 [02:15<00:22, 143.99patch/s]
79%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 11757/14940 [02:15<00:21, 147.54patch/s]
79%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 11772/14940 [02:15<00:21, 144.75patch/s]
79%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 11788/14940 [02:15<00:21, 147.29patch/s]
79%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 11804/14940 [02:16<00:21, 149.31patch/s]
79%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 11820/14940 [02:16<00:20, 150.87patch/s]
79%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 11836/14940 [02:16<00:20, 149.73patch/s]
79%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 11851/14940 [02:16<00:21, 144.79patch/s]
79%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 11866/14940 [02:16<00:21, 145.23patch/s]
80%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 11882/14940 [02:16<00:20, 147.56patch/s]
80%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 11898/14940 [02:16<00:20, 150.49patch/s]
80%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 11914/14940 [02:16<00:19, 152.59patch/s]
80%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 11930/14940 [02:16<00:19, 154.75patch/s]
80%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 11947/14940 [02:17<00:19, 156.69patch/s]
80%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 11963/14940 [02:17<00:19, 156.51patch/s]
80%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 11979/14940 [02:17<00:19, 155.02patch/s]
80%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 11995/14940 [02:17<00:18, 155.79patch/s]
80%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 12012/14940 [02:17<00:18, 156.82patch/s]
81%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 12028/14940 [02:17<00:18, 157.53patch/s]
81%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 12045/14940 [02:17<00:18, 158.62patch/s]
81%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 12061/14940 [02:17<00:18, 158.78patch/s]
81%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 12077/14940 [02:17<00:18, 158.90patch/s]
81%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 12094/14940 [02:17<00:17, 159.58patch/s]
81%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 12110/14940 [02:18<00:17, 159.46patch/s]
81%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 12126/14940 [02:18<00:17, 159.38patch/s]
81%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 12143/14940 [02:18<00:17, 159.91patch/s]
81%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 12159/14940 [02:18<00:17, 159.23patch/s]
81%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 12175/14940 [02:18<00:17, 158.74patch/s]
82%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 12191/14940 [02:18<00:17, 158.41patch/s]
82%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 12207/14940 [02:18<00:17, 158.17patch/s]
82%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 12224/14940 [02:18<00:17, 159.07patch/s]
82%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 12240/14940 [02:18<00:16, 159.10patch/s]
82%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 12257/14940 [02:18<00:16, 160.19patch/s]
82%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 12274/14940 [02:19<00:16, 160.47patch/s]
82%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 12291/14940 [02:19<00:18, 142.17patch/s]
82%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 12306/14940 [02:19<00:22, 117.94patch/s]
82%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 12319/14940 [02:19<00:27, 96.87patch/s]
83%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 12330/14940 [02:19<00:28, 92.14patch/s]
83%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 12340/14940 [02:19<00:29, 87.06patch/s]
83%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 12350/14940 [02:20<00:31, 81.98patch/s]
83%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 12359/14940 [02:20<00:31, 80.76patch/s]
83%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 12368/14940 [02:20<00:33, 77.79patch/s]
83%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 12376/14940 [02:20<00:33, 76.97patch/s]
83%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 12385/14940 [02:20<00:32, 78.40patch/s]
83%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 12394/14940 [02:20<00:32, 79.41patch/s]
83%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 12403/14940 [02:20<00:31, 80.43patch/s]
83%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 12412/14940 [02:20<00:31, 81.08patch/s]
83%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 12421/14940 [02:20<00:31, 80.91patch/s]
83%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 12430/14940 [02:21<00:31, 80.65patch/s]
83%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 12439/14940 [02:21<00:30, 81.07patch/s]
83%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 12448/14940 [02:21<00:30, 81.18patch/s]
83%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 12457/14940 [02:21<00:30, 81.89patch/s]
83%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 12466/14940 [02:21<00:33, 72.96patch/s]
83%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 12474/14940 [02:21<00:33, 73.39patch/s]
84%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 12482/14940 [02:21<00:32, 75.08patch/s]
84%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 12490/14940 [02:21<00:32, 76.12patch/s]
84%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 12499/14940 [02:21<00:31, 77.41patch/s]
84%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 12508/14940 [02:22<00:30, 78.54patch/s]
84%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 12517/14940 [02:22<00:30, 80.01patch/s]
84%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 12526/14940 [02:22<00:29, 81.10patch/s]
84%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 12535/14940 [02:22<00:30, 79.28patch/s]
84%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 12544/14940 [02:22<00:30, 79.65patch/s]
84%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 12552/14940 [02:22<00:30, 79.16patch/s]
84%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 12560/14940 [02:22<00:30, 76.79patch/s]
84%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 12568/14940 [02:22<00:30, 76.91patch/s]
84%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 12577/14940 [02:22<00:30, 77.89patch/s]
84%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 12585/14940 [02:23<00:30, 77.43patch/s]
84%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 12594/14940 [02:23<00:29, 79.04patch/s]
84%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 12602/14940 [02:23<00:29, 79.28patch/s]
84%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 12610/14940 [02:23<00:29, 79.24patch/s]
84%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 12618/14940 [02:23<00:29, 79.11patch/s]
85%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 12626/14940 [02:23<00:29, 78.46patch/s]
85%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 12634/14940 [02:23<00:29, 78.69patch/s]
85%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 12642/14940 [02:23<00:29, 78.98patch/s]
85%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 12651/14940 [02:23<00:28, 79.47patch/s]
85%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 12660/14940 [02:23<00:28, 80.24patch/s]
85%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 12669/14940 [02:24<00:28, 78.31patch/s]
85%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 12678/14940 [02:24<00:28, 79.12patch/s]
85%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 12687/14940 [02:24<00:29, 76.84patch/s]
85%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 12696/14940 [02:24<00:28, 78.19patch/s]
85%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 12704/14940 [02:24<00:30, 72.26patch/s]
85%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 12713/14940 [02:24<00:29, 75.24patch/s]
85%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 12721/14940 [02:24<00:31, 70.69patch/s]
85%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 12729/14940 [02:24<00:30, 71.71patch/s]
85%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 12738/14940 [02:25<00:29, 74.56patch/s]
85%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 12746/14940 [02:25<00:34, 63.17patch/s]
85%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 12755/14940 [02:25<00:32, 67.82patch/s]
85%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 12763/14940 [02:25<00:33, 65.84patch/s]
85%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 12771/14940 [02:25<00:31, 69.13patch/s]
86%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 12780/14940 [02:25<00:29, 72.49patch/s]
86%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 12789/14940 [02:25<00:28, 75.29patch/s]
86%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 12797/14940 [02:25<00:30, 70.44patch/s]
86%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 12806/14940 [02:26<00:28, 73.80patch/s]
86%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 12815/14940 [02:26<00:27, 76.23patch/s]
86%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 12824/14940 [02:26<00:27, 77.42patch/s]
86%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 12832/14940 [02:26<00:27, 77.60patch/s]
86%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 12841/14940 [02:26<00:26, 78.52patch/s]
86%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 12850/14940 [02:26<00:26, 79.43patch/s]
86%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 12858/14940 [02:26<00:27, 74.72patch/s]
86%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 12866/14940 [02:26<00:28, 72.12patch/s]
86%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 12874/14940 [02:26<00:28, 73.49patch/s]
86%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 12882/14940 [02:27<00:28, 73.13patch/s]
86%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 12890/14940 [02:27<00:28, 73.12patch/s]
86%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 12898/14940 [02:27<00:27, 73.25patch/s]
86%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 12906/14940 [02:27<00:27, 72.90patch/s]
86%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 12914/14940 [02:27<00:27, 74.70patch/s]
86%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 12923/14940 [02:27<00:26, 76.51patch/s]
87%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 12932/14940 [02:27<00:25, 77.78patch/s]
87%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 12941/14940 [02:27<00:25, 79.18patch/s]
87%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 12950/14940 [02:27<00:24, 79.76patch/s]
87%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 12959/14940 [02:28<00:24, 80.51patch/s]
87%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 12968/14940 [02:28<00:24, 80.48patch/s]
87%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 12977/14940 [02:28<00:24, 80.54patch/s]
87%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 12986/14940 [02:28<00:24, 80.78patch/s]
87%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 12995/14940 [02:28<00:24, 78.90patch/s]
87%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 13004/14940 [02:28<00:24, 80.49patch/s]
87%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 13013/14940 [02:28<00:23, 81.38patch/s]
87%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 13022/14940 [02:28<00:23, 81.89patch/s]
87%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 13031/14940 [02:28<00:23, 81.46patch/s]
87%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 13040/14940 [02:28<00:23, 81.91patch/s]
87%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 13049/14940 [02:29<00:22, 82.50patch/s]
87%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 13058/14940 [02:29<00:22, 82.18patch/s]
87%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 13067/14940 [02:29<00:22, 82.11patch/s]
88%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 13076/14940 [02:29<00:23, 80.05patch/s]
88%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 13085/14940 [02:29<00:23, 80.56patch/s]
88%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 13094/14940 [02:29<00:23, 80.04patch/s]
88%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 13103/14940 [02:29<00:28, 63.43patch/s]
88%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 13111/14940 [02:29<00:27, 66.43patch/s]
88%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 13119/14940 [02:30<00:26, 69.66patch/s]
88%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 13128/14940 [02:30<00:24, 73.05patch/s]
88%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 13137/14940 [02:30<00:23, 75.22patch/s]
88%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 13146/14940 [02:30<00:23, 77.28patch/s]
88%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 13155/14940 [02:30<00:22, 79.08patch/s]
88%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 13164/14940 [02:30<00:21, 80.91patch/s]
88%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 13173/14940 [02:30<00:21, 81.65patch/s]
88%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 13182/14940 [02:30<00:21, 81.40patch/s]
88%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 13191/14940 [02:30<00:21, 82.22patch/s]
88%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 13200/14940 [02:31<00:21, 81.87patch/s]
88%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 13209/14940 [02:31<00:21, 81.28patch/s]
88%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 13218/14940 [02:31<00:21, 80.21patch/s]
89%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 13227/14940 [02:31<00:22, 76.77patch/s]
89%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 13235/14940 [02:31<00:22, 76.33patch/s]
89%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 13244/14940 [02:31<00:21, 77.43patch/s]
89%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 13253/14940 [02:31<00:21, 78.89patch/s]
89%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 13262/14940 [02:31<00:21, 79.40patch/s]
89%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 13271/14940 [02:31<00:20, 79.99patch/s]
89%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 13280/14940 [02:32<00:20, 80.30patch/s]
89%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 13289/14940 [02:32<00:20, 80.81patch/s]
89%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 13298/14940 [02:32<00:20, 81.61patch/s]
89%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 13307/14940 [02:32<00:20, 81.54patch/s]
89%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 13316/14940 [02:32<00:19, 81.67patch/s]
89%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 13325/14940 [02:32<00:19, 82.27patch/s]
89%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 13334/14940 [02:32<00:19, 82.82patch/s]
89%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 13343/14940 [02:32<00:19, 83.04patch/s]
89%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 13352/14940 [02:32<00:19, 82.88patch/s]
89%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 13361/14940 [02:33<00:19, 82.65patch/s]
89%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 13370/14940 [02:33<00:19, 82.50patch/s]
90%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 13379/14940 [02:33<00:18, 82.60patch/s]
90%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 13388/14940 [02:33<00:18, 82.43patch/s]
90%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 13397/14940 [02:33<00:18, 82.59patch/s]
90%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 13406/14940 [02:33<00:18, 82.32patch/s]
90%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 13415/14940 [02:33<00:18, 81.70patch/s]
90%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 13424/14940 [02:33<00:18, 81.72patch/s]
90%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 13433/14940 [02:33<00:18, 81.45patch/s]
90%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 13442/14940 [02:34<00:18, 80.82patch/s]
90%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 13451/14940 [02:34<00:19, 77.20patch/s]
90%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 13459/14940 [02:34<00:19, 77.84patch/s]
90%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 13468/14940 [02:34<00:18, 79.02patch/s]
90%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 13477/14940 [02:34<00:18, 80.49patch/s]
90%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 13486/14940 [02:34<00:17, 81.66patch/s]
90%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 13495/14940 [02:34<00:17, 82.04patch/s]
90%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 13504/14940 [02:34<00:17, 82.76patch/s]
90%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 13513/14940 [02:34<00:17, 83.27patch/s]
91%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 13522/14940 [02:35<00:16, 83.51patch/s]
91%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 13531/14940 [02:35<00:17, 82.74patch/s]
91%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 13540/14940 [02:35<00:16, 82.88patch/s]
91%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 13549/14940 [02:35<00:17, 79.64patch/s]
91%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 13558/14940 [02:35<00:17, 80.96patch/s]
91%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 13567/14940 [02:35<00:17, 80.67patch/s]
91%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 13576/14940 [02:35<00:16, 80.75patch/s]
91%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 13585/14940 [02:35<00:17, 77.59patch/s]
91%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 13593/14940 [02:35<00:17, 75.61patch/s]
91%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 13601/14940 [02:36<00:17, 74.56patch/s]
91%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 13609/14940 [02:36<00:17, 74.28patch/s]
91%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 13617/14940 [02:36<00:17, 73.61patch/s]
91%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 13625/14940 [02:36<00:17, 73.84patch/s]
91%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 13633/14940 [02:36<00:17, 73.66patch/s]
91%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 13641/14940 [02:36<00:17, 73.26patch/s]
91%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 13649/14940 [02:36<00:17, 73.40patch/s]
91%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 13657/14940 [02:36<00:17, 72.69patch/s]
91%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 13665/14940 [02:36<00:17, 73.49patch/s]
92%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 13674/14940 [02:37<00:16, 76.20patch/s]
92%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 13683/14940 [02:37<00:16, 78.42patch/s]
92%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 13692/14940 [02:37<00:15, 79.84patch/s]
92%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 13700/14940 [02:37<00:15, 79.43patch/s]
92%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 13709/14940 [02:37<00:15, 79.92patch/s]
92%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 13718/14940 [02:37<00:15, 80.71patch/s]
92%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 13727/14940 [02:37<00:14, 81.57patch/s]
92%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 13736/14940 [02:37<00:14, 82.62patch/s]
92%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 13745/14940 [02:37<00:14, 81.71patch/s]
92%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 13754/14940 [02:38<00:14, 82.29patch/s]
92%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 13763/14940 [02:38<00:14, 81.47patch/s]
92%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 13772/14940 [02:38<00:14, 81.48patch/s]
92%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 13781/14940 [02:38<00:14, 78.95patch/s]
92%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 13789/14940 [02:38<00:14, 79.01patch/s]
92%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 13797/14940 [02:38<00:14, 78.28patch/s]
92%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 13805/14940 [02:38<00:15, 73.54patch/s]
92%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 13814/14940 [02:38<00:14, 76.44patch/s]
93%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 13822/14940 [02:38<00:15, 71.44patch/s]
93%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 13831/14940 [02:39<00:14, 74.43patch/s]
93%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 13839/14940 [02:39<00:15, 73.20patch/s]
93%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 13847/14940 [02:39<00:14, 74.64patch/s]
93%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 13855/14940 [02:39<00:14, 75.98patch/s]
93%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 13863/14940 [02:39<00:14, 71.94patch/s]
93%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 13872/14940 [02:39<00:14, 74.62patch/s]
93%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 13880/14940 [02:39<00:14, 75.57patch/s]
93%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 13889/14940 [02:39<00:13, 77.24patch/s]
93%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 13897/14940 [02:39<00:14, 70.20patch/s]
93%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 13906/14940 [02:40<00:14, 73.19patch/s]
93%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 13914/14940 [02:40<00:13, 74.92patch/s]
93%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 13923/14940 [02:40<00:13, 76.60patch/s]
93%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 13932/14940 [02:40<00:13, 77.53patch/s]
93%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 13940/14940 [02:40<00:12, 78.15patch/s]
93%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 13949/14940 [02:40<00:12, 79.02patch/s]
93%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 13958/14940 [02:40<00:12, 79.26patch/s]
93%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 13967/14940 [02:40<00:12, 80.13patch/s]
94%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 13976/14940 [02:40<00:12, 80.19patch/s]
94%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 13985/14940 [02:41<00:11, 80.34patch/s]
94%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 13994/14940 [02:41<00:11, 81.12patch/s]
94%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 14003/14940 [02:41<00:11, 80.86patch/s]
94%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 14012/14940 [02:41<00:11, 81.19patch/s]
94%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 14021/14940 [02:41<00:11, 81.02patch/s]
94%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 14030/14940 [02:41<00:11, 81.50patch/s]
94%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 14039/14940 [02:41<00:10, 82.38patch/s]
94%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 14048/14940 [02:41<00:10, 82.17patch/s]
94%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 14057/14940 [02:41<00:10, 82.19patch/s]
94%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 14066/14940 [02:42<00:10, 82.32patch/s]
94%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 14075/14940 [02:42<00:10, 82.37patch/s]
94%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 14084/14940 [02:42<00:10, 81.44patch/s]
94%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 14093/14940 [02:42<00:10, 81.55patch/s]
94%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 14102/14940 [02:42<00:10, 82.05patch/s]
94%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 14111/14940 [02:42<00:09, 82.99patch/s]
95%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 14120/14940 [02:42<00:09, 83.38patch/s]
95%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 14129/14940 [02:42<00:09, 82.38patch/s]
95%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 14138/14940 [02:42<00:09, 82.17patch/s]
95%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 14147/14940 [02:43<00:09, 80.93patch/s]
95%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 14156/14940 [02:43<00:09, 81.38patch/s]
95%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 14165/14940 [02:43<00:09, 79.39patch/s]
95%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 14174/14940 [02:43<00:09, 79.88patch/s]
95%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 14183/14940 [02:43<00:09, 80.35patch/s]
95%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 14192/14940 [02:43<00:09, 80.40patch/s]
95%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 14201/14940 [02:43<00:09, 80.52patch/s]
95%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 14210/14940 [02:43<00:09, 76.61patch/s]
95%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 14219/14940 [02:43<00:09, 77.88patch/s]
95%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 14228/14940 [02:44<00:09, 79.02patch/s]
95%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 14237/14940 [02:44<00:08, 79.62patch/s]
95%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 14246/14940 [02:44<00:08, 80.26patch/s]
95%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 14255/14940 [02:44<00:08, 80.96patch/s]
95%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 14264/14940 [02:44<00:08, 81.23patch/s]
96%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 14273/14940 [02:44<00:08, 81.99patch/s]
96%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 14282/14940 [02:44<00:08, 81.65patch/s]
96%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 14291/14940 [02:44<00:07, 81.28patch/s]
96%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 14300/14940 [02:44<00:07, 81.37patch/s]
96%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 14309/14940 [02:45<00:07, 81.83patch/s]
96%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 14318/14940 [02:45<00:07, 82.84patch/s]
96%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 14327/14940 [02:45<00:07, 82.91patch/s]
96%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 14336/14940 [02:45<00:07, 81.69patch/s]
96%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 14345/14940 [02:45<00:07, 74.99patch/s]
96%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 14354/14940 [02:45<00:07, 76.94patch/s]
96%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 14363/14940 [02:45<00:07, 78.78patch/s]
96%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 14371/14940 [02:45<00:07, 78.58patch/s]
96%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 14380/14940 [02:45<00:06, 80.09patch/s]
96%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 14389/14940 [02:46<00:06, 81.42patch/s]
96%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 14398/14940 [02:46<00:06, 82.10patch/s]
96%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 14407/14940 [02:46<00:06, 82.16patch/s]
96%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 14416/14940 [02:46<00:06, 82.50patch/s]
97%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 14425/14940 [02:46<00:06, 81.59patch/s]
97%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 14434/14940 [02:46<00:06, 82.21patch/s]
97%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 14443/14940 [02:46<00:06, 79.19patch/s]
97%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 14452/14940 [02:46<00:06, 80.54patch/s]
97%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 14461/14940 [02:46<00:05, 80.09patch/s]
97%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 14470/14940 [02:47<00:05, 79.93patch/s]
97%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 14479/14940 [02:47<00:05, 79.68patch/s]
97%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 14487/14940 [02:47<00:06, 74.59patch/s]
97%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 14495/14940 [02:47<00:06, 72.95patch/s]
97%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 14504/14940 [02:47<00:05, 76.70patch/s]
97%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 14513/14940 [02:47<00:05, 78.61patch/s]
97%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 14522/14940 [02:47<00:05, 79.71patch/s]
97%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 14531/14940 [02:47<00:05, 80.67patch/s]
97%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 14540/14940 [02:47<00:04, 81.36patch/s]
97%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 14549/14940 [02:48<00:04, 81.35patch/s]
97%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 14558/14940 [02:48<00:04, 81.06patch/s]
98%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 14567/14940 [02:48<00:04, 80.63patch/s]
98%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 14576/14940 [02:48<00:04, 80.18patch/s]
98%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 14585/14940 [02:48<00:04, 75.55patch/s]
98%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 14594/14940 [02:48<00:04, 77.29patch/s]
98%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 14602/14940 [02:48<00:04, 77.99patch/s]
98%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 14610/14940 [02:48<00:04, 77.79patch/s]
98%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 14619/14940 [02:48<00:04, 78.42patch/s]
98%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 14628/14940 [02:49<00:03, 79.32patch/s]
98%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 14637/14940 [02:49<00:03, 80.21patch/s]
98%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 14646/14940 [02:49<00:03, 80.78patch/s]
98%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 14655/14940 [02:49<00:03, 80.04patch/s]
98%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 14664/14940 [02:49<00:03, 77.66patch/s]
98%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 14672/14940 [02:49<00:03, 78.19patch/s]
98%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 14680/14940 [02:49<00:03, 77.95patch/s]
98%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 14688/14940 [02:49<00:03, 77.44patch/s]
98%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 14696/14940 [02:49<00:03, 76.44patch/s]
98%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 14705/14940 [02:50<00:03, 76.86patch/s]
98%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 14713/14940 [02:50<00:03, 66.08patch/s]
99%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 14720/14940 [02:50<00:03, 65.08patch/s]
99%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 14728/14940 [02:50<00:03, 66.90patch/s]
99%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 14735/14940 [02:50<00:03, 67.57patch/s]
99%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 14742/14940 [02:50<00:03, 63.86patch/s]
99%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 14750/14940 [02:50<00:02, 67.44patch/s]
99%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 14757/14940 [02:50<00:02, 66.13patch/s]
99%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 14764/14940 [02:50<00:02, 65.59patch/s]
99%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 14772/14940 [02:51<00:02, 67.33patch/s]
99%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 14779/14940 [02:51<00:02, 67.95patch/s]
99%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 14786/14940 [02:51<00:02, 67.76patch/s]
99%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 14793/14940 [02:51<00:02, 67.95patch/s]
99%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 14801/14940 [02:51<00:02, 68.93patch/s]
99%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 14809/14940 [02:51<00:01, 70.03patch/s]
99%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 14817/14940 [02:51<00:01, 70.07patch/s]
99%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 14825/14940 [02:51<00:01, 71.88patch/s]
99%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 14833/14940 [02:51<00:01, 72.34patch/s]
99%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 14841/14940 [02:52<00:01, 69.99patch/s]
99%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 14849/14940 [02:52<00:01, 70.70patch/s]
99%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 14857/14940 [02:52<00:01, 71.14patch/s]
100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏| 14866/14940 [02:52<00:00, 74.14patch/s]
100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎| 14874/14940 [02:52<00:00, 75.44patch/s]
100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎| 14882/14940 [02:52<00:00, 75.28patch/s]
100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍| 14890/14940 [02:52<00:00, 75.59patch/s]
100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌| 14898/14940 [02:52<00:00, 75.50patch/s]
100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋| 14906/14940 [02:52<00:00, 73.08patch/s]
100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋| 14914/14940 [02:53<00:00, 73.25patch/s]
100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊| 14922/14940 [02:53<00:00, 74.55patch/s]
100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉| 14931/14940 [02:53<00:00, 76.29patch/s]
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 14940/14940 [02:53<00:00, 77.83patch/s]
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 14940/14940 [02:53<00:00, 86.17patch/s]
False
<mne.viz._brain._brain.Brain object at 0x000002338C37D370>
Plot the RSA timecourse at the peak vertex
plt.figure()
plt.plot(rsa_vals.times, rsa_vals.data[peak_vertex])
plt.xlabel("Time (s)")
plt.ylabel("Kendall-Tau (alpha)")
plt.title(f"RSA values at vert {peak_vertex}")
Text(0.5, 1.0, 'RSA values at vert 127')
Total running time of the script: (3 minutes 23.420 seconds)