Solving problems with CNF SAT solvers: The Sudoku example

We now show one example on how CF formulas and modern SAT solvers can be used to solve other computationally difficult problems. The following material is partly a recap from the Aalto courses CS-A1140 Data Structures and Algorithms and CS-E4800 Artificial Intelligence.

In a \(9 \times 9\) Sudoku, one has to complete a partially filled \(9 \times 9\) grid with the numbers \(1,...,9\) so that

each row contains the numbers \(1,...,9\),
each column contains the numbers \(1,...,9\), and
each of the disjoint \(3 \times 3\) sub-grids contain the numbers \(1,...,9\).

As an example, the unique solution to the Sudoku puzzle

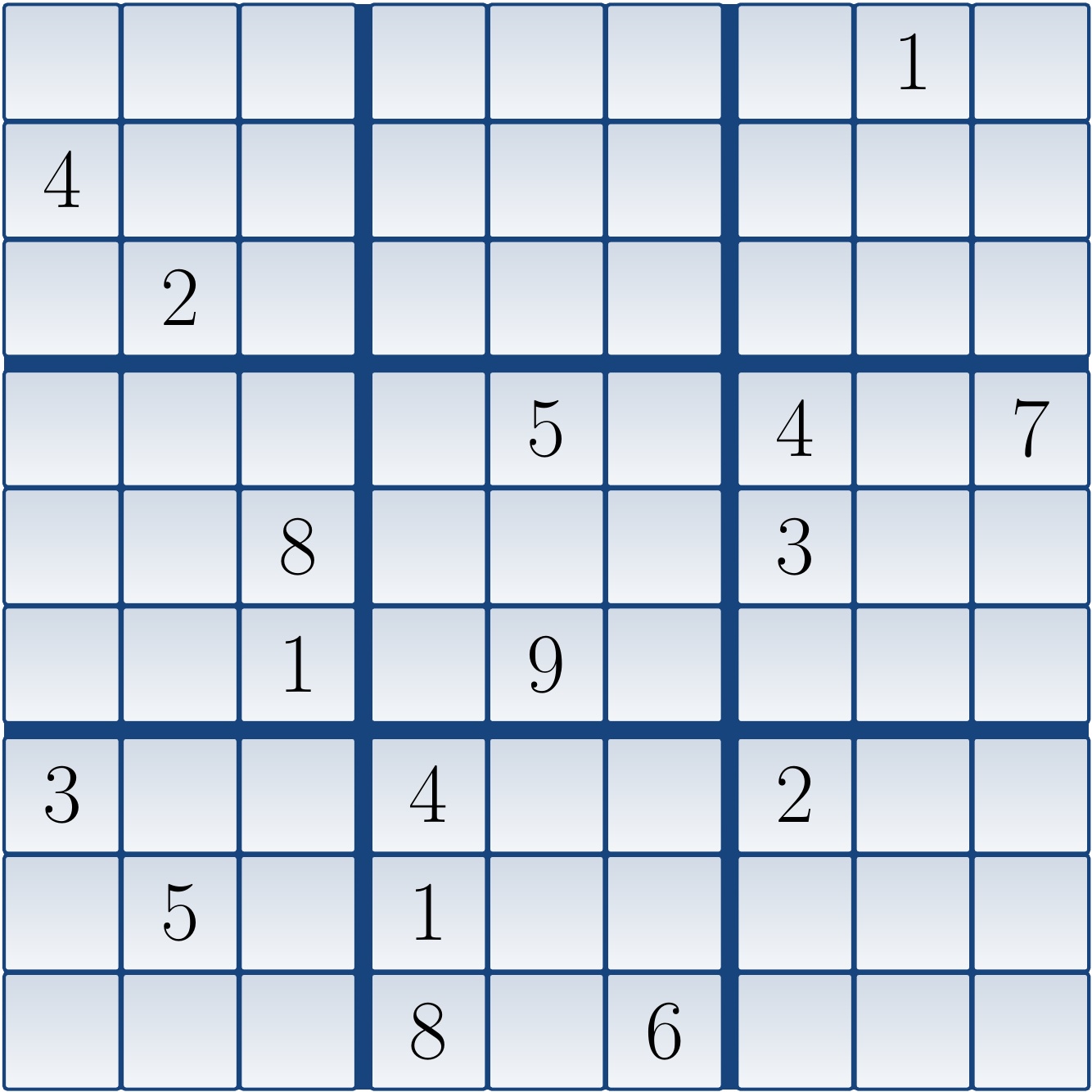
is

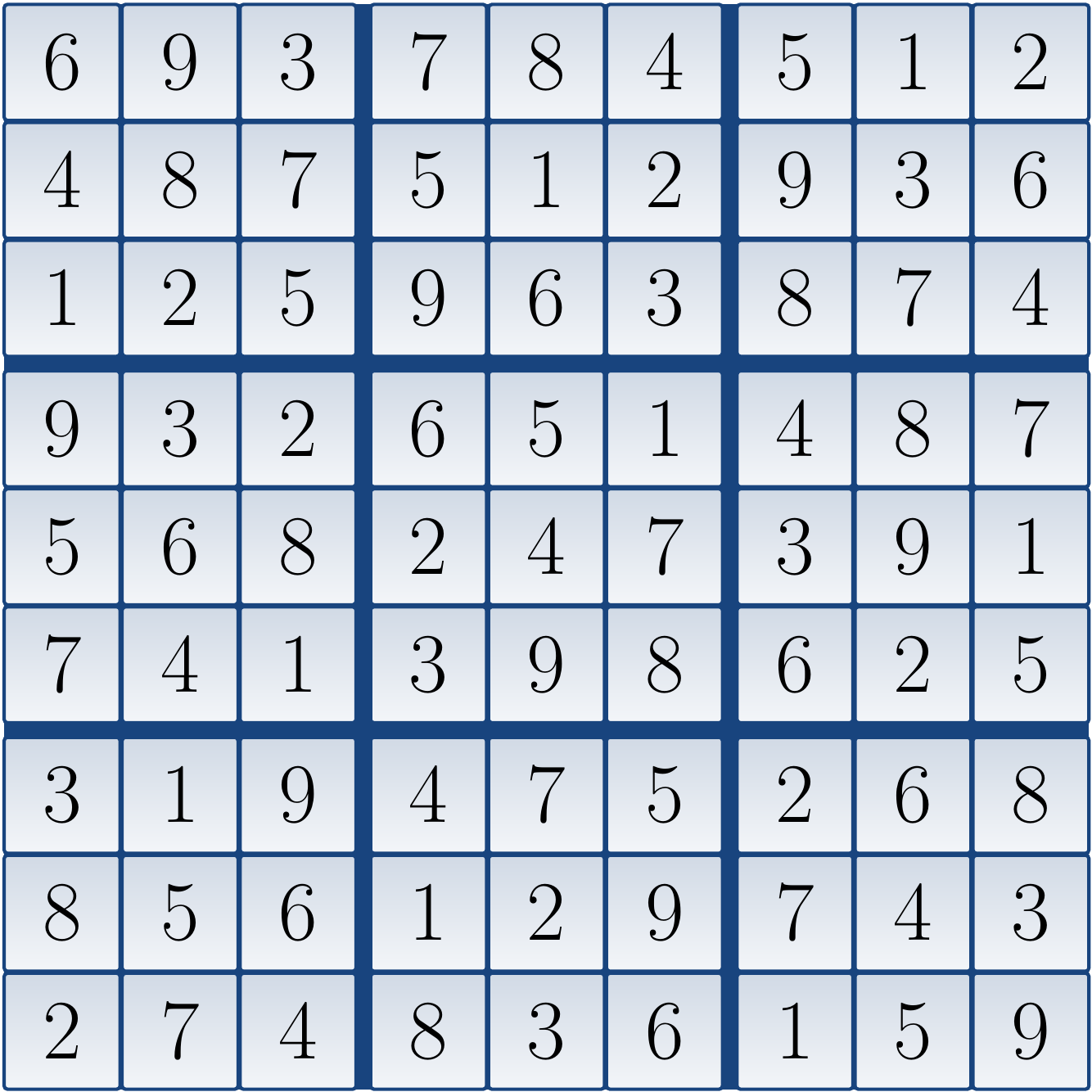
The Sudoku puzzle above is taken from Gordon Royle’s minimum Sudoku collection. It has 17 clues, puzzles with 16 or less clues do not exist (the solution for the puzzle must be unique).

In imperative and functional programming, Sudokus could be solved by programming a custom backtracking search algorithm (recall the “Recursion” round of CS-A1120 Programming 2). In constraint programming, however, we

encode the problem in a constraint language, and
let the constraint solver find the solution (or report that none exists).

In this first round, we use

propositional satisfiability as the constraint language, and
modern, highly efficient SAT solvers as the constraint solvers.

We thus reduce the problem of solving Sudokus to the propositional satisfiability problem and the workflow looks like this:

Encoding Sudoku in CNF

Suppose that we are given an \(n \times n\) Sudoku puzzle, where the dimension \(n=d^2\) for some positive integer \(d\). Our goal is now to build a propositional formula \(\phi\) such that

the Sudoku puzzle has a solution if and only if the formula is satisfiable, and
from a satisfying assignment for \(\phi\) we can easily decode a solution for the Sudoku puzzle.

To obtain such a formula, we first introduce a variable

\[\SUD{r}{c}{v}\]

for each row \(r = [1..n]\), column \(c \in [1..n]\) and value \(v \in [1..n]\). The intuition is that if \(\SUD{r}{c}{v}\) is true, then the grid element at row \(r\) and column \(c\) has the value \(v\). To enforce that the values of the variables \(\SUD{r}{c}{v}\) model solutions to the Sudoku puzzle, the formula

\[\phi = C_1 \land C_2 \land C_3 \land C_4 \land C_5 \land C_6\]

is built by introducing sets of clauses that model different aspects of Sudoku solutions:

Each entry has at least one value: \(C_1 = \bigwedge_{r,c \in [1..n]}(\SUD{r}{c}{1} \lor \SUD{r}{c}{2} \lor ... \lor \SUD{r}{c}{n})\)
Each entry has at most one value: \(C_2 = \bigwedge_{r,c,v,v' \in [1..n] \textup{ with } v < v'}(\neg\SUD{r}{c}{v} \lor \neg\SUD{r}{c}{v'})\)
Each row has all the numbers: \(C_3 = \bigwedge_{r,v \in [1..n]}(\SUD{r}{1}{v} \lor \SUD{r}{2}{v} \lor ... \lor \SUD{r}{n}{v})\)
Each column has all the numbers: \(C_4 = \bigwedge_{c,v \in [1..n]}(\SUD{1}{c}{v} \lor \SUD{2}{c}{v} \lor ... \lor \SUD{n}{c}{v})\)
Each disjoint sub-grid has all the numbers: \(C_5 = \bigwedge_{r',c' \in [1..d], v \in [1..n]}(\bigvee_{(r,c) \in B_d(r'-1,c'-1)}\SUD{r}{c}{v})\) where \(B_d(r',c') = \Setdef{(r'd+i,c'd+j)}{i,j \in [1..d]}\)
The solution respects the given clues \(\SUDClues\): \(C_6 = \bigwedge_{(r,c,v) \in \SUDClues}(\SUD{r}{c}{v})\)

Note

Unlike in imperative programming, we do not give values for the variables, they are “unknowns”. It is the task of the constraint solver to find whether they can have some values that respect all the constraints (i.e., clauses in the case of CNF formula satisfiability).

The resulting formula has \(\Card{\SUDClues}\) unary clauses, \(n^2\frac{n(n-1)}{2}\) binary clauses, and \(4n^2\) clauses of length \(n\). Thus the size of the formula is polynomial in the grid dimension \(n\).

Example

Consider the Sudoku puzzle

The corresponding CNF formula is:

\begin{eqnarray*} (x_{1,1,1} \lor x_{1,1,2} \lor ... \lor x_{1,1,9}) \land ... \land (x_{9,9,1} \lor x_{9,9,2} \lor ... \lor x_{9,9,9}) \land {}&&\\ (\neg x_{1,1,1} \lor \neg x_{1,1,2}) \land ... \land (\neg x_{9,9,8} \lor \neg x_{9,9,9}) \land{}&&\\ (x_{1,1,1} \lor x_{1,2,1} \lor ... \lor x_{1,9,1}) \land ... \land (x_{9,1,9} \lor x_{9,2,9} \lor ... \lor x_{9,9,9}) \land {}&&\\ (x_{1,1,1} \lor x_{2,1,1} \lor ... \lor x_{9,1,1}) \land ... \land (x_{1,9,9} \lor x_{2,9,9} \lor ... \lor x_{9,9,9}) \land {}&&\\ (x_{1,1,1} \lor x_{1,2,1} \lor ... \lor x_{3,3,1}) \land ... \land (x_{7,7,9} \lor x_{7,8,9} \lor ... \lor x_{9,9,9}) \land {}&&\\ (x_{1,8,1}) \land (x_{2,1,4}) \land (x_{3,2,2}) \land ... \land (x_{9,6,6})&& \end{eqnarray*}

The DIMACS CNF file format

The DIMACS CNF format is a simple file format for storing CNF formulas. It is supported by practically all modern SAT solvers and it is also used in the regularly organized SAT Competitions that benchmarks the best solvers against each other. The format can be described as follows:

Lines starting with c are comments.
The header line of form p cnf n m declares that the problem consists of \(n\) variables \(x_1,...,x_n\) and \(m\) clauses.
The following lines describe the clauses. A clause \((l_1 \lor l_2 \lor ... \lor l_k)\) is written as v1 v2 ... vn 0, where
- each integer v\(i\) is (a) \(j\) if \(l_i\) is the positive literal \(x_j\), and (b) \(-j\) if \(l_i\) is the negative literal \(\neg x_j\), and
- the last 0 marks the end of the clause.

Example

The CNF formula

\[(\neg x_1 \lor x_2) \land (\neg x_1 \lor x_3) \land (x_1 \lor \neg x_2 \lor \neg x_3)\]

is given in the DIMACS representation as follows:

c Comments are ignored
p cnf 3 3
-1 2 0
-1 3 0
1 -2 -3 0

The DIMACS CNF format is not very nice for encoding problems by hand. Thus one usually automatically generates such a file with some script program. For instance, CNF instances for Sudoku puzzles could be generated by the following Python program sudoku-encode.py:

#!/usr/bin/python3
import sys
D = 3    # Subgrid dimension
N = D*D  # Grid dimension

# The symbols allowed in the Sudoku instance text file
DIGITS = {'1':1, '2':2, '3':3, '4':4, '5':5, '6':6, '7':7, '8':8, '9':9}
NOCLUE = '.'

def read_clues(filename: str):
    """Read a Sudoku instance (a set of clues) from a file."""
    clues = []
    with open(filename, 'r', encoding='UTF-8') as handle:
        for line in handle.readlines():
            line = line.strip()
            assert len(line) == N, f'Malformed line "{line}"'
            for column in range(0, N):
                assert line[column] in DIGITS.keys() or line[column] == NOCLUE
            clues.append(line.strip())
    assert len(clues) == N
    return clues

def encode(clues):
    """Encode the given clueas as DIMACS CNF SAT instance
    in the standard output."""

    def var(row: int, column: int, value: int):
        """A helper: get the DIMACS CNF variable number for
        the variable v_{row,column,value} encoding the fact that
        the cell at (row,column) has the value "value"."""
        assert 1 <= row <= N and 1 <= column <= N and 1 <= value <= N
        return (row-1)*N*N+(column-1)*N+(value-1)+1

    # Build the clauses in a list
    clauses = []  # The clauses: a list of integer lists
    for row in range(1, N+1): # row runs over 1,...,N
        for column in range(1, N+1):
            # The cell at (row,column) has at least one value
            clauses.append([var(row, column, value) for value in range(1, N+1)])
            # The cell at (row,column) has at most one value
            for value in range(1, N+1):
                for walue in range(value+1, N+1):
                    clauses.append([-var(row, column, value),
                                    -var(row, column, walue)])
    for value in range(1, N+1):
        # Each row has the value
        for row in range(1, N+1):
            clauses.append([var(row, column, value) for column in range(1, N+1)])
        # Each column has the value
        for column in range(1, N+1):
            clauses.append([var(row, column, value) for row in range(1, N+1)])
        # Each subgrid has the value
        for sr in range(0, D):
            for sc in range(0, D):
                clauses.append([var(sr*D+rd, sc*D+cd, value)
                                for rd in range(1, D+1)
                                for cd in range(1, D+1)])
    # The clues must be respected
    for row in range(1, N+1):
        for column in range(1, N+1):
            clue = clues[row-1][column-1]
            if clue in DIGITS.keys():
                clauses.append([var(row, column, DIGITS[clue])])

    # Output the DIMACS CNF representation
    # Print the header line
    print('p cnf %d %d' % (N*N*N, len(clauses)))
    # Print the clauses
    for clause in clauses:
        print(' '.join([str(lit) for lit in clause])+' 0')

if __name__ == '__main__':
    # Read the clues from the file given as the first argument,
    # and encode them as a CNF SAT instance
    encode(read_clues(sys.argv[1]))

The data files describing the actual puzzles are of the form illustrated in the example file sudoku-royle.txt below.

.......1.
4........
.2.......
....5.4.7
..8...3..
..1.9....
3..4..2..
.5.1.....
...8.6...

Running the program on Linux with the clasp SAT solver, we get the following output.

python3 sudoku-encode.py sudoku-royle.txt | clasp -n 0
c clasp version 3.3.3
c Reading from stdin
c Solving...
c Answer: 1
v -1 -2 -3 -4 -5 6 -7 -8 -9 -10 -11 -12 -13 -14 -15 -16 -17 18 -19 -20 21
v -22 -23 -24 -25 -26 -27 -28 -29 -30 -31 -32 -33 34 -35 -36 -37 -38 -39
v -40 -41 -42 -43 44 -45 -46 -47 -48 49 -50 -51 -52 -53 -54 -55 -56 -57 -58
v 59 -60 -61 -62 -63 64 -65 -66 -67 -68 -69 -70 -71 -72 -73 74 -75 -76 -77
v -78 -79 -80 -81 -82 -83 -84 85 -86 -87 -88 -89 -90 -91 -92 -93 -94 -95
v -96 -97 98 -99 -100 -101 -102 -103 -104 -105 106 -107 -108 -109 -110 -111
v -112 113 -114 -115 -116 -117 118 -119 -120 -121 -122 -123 -124 -125 -126
v -127 128 -129 -130 -131 -132 -133 -134 -135 -136 -137 -138 -139 -140 -141
v -142 -143 144 -145 -146 147 -148 -149 -150 -151 -152 -153 -154 -155 -156
v -157 -158 159 -160 -161 -162 163 -164 -165 -166 -167 -168 -169 -170 -171
v -172 173 -174 -175 -176 -177 -178 -179 -180 -181 -182 -183 -184 185 -186
v -187 -188 -189 -190 -191 -192 -193 -194 -195 -196 -197 198 -199 -200 -201
v -202 -203 204 -205 -206 -207 -208 -209 210 -211 -212 -213 -214 -215 -216
v -217 -218 -219 -220 -221 -222 -223 224 -225 -226 -227 -228 -229 -230 -231
v 232 -233 -234 -235 -236 -237 238 -239 -240 -241 -242 -243 -244 -245 -246
v -247 -248 -249 -250 -251 252 -253 -254 255 -256 -257 -258 -259 -260 -261
v -262 263 -264 -265 -266 -267 -268 -269 -270 -271 -272 -273 -274 -275 276
v -277 -278 -279 -280 -281 -282 -283 284 -285 -286 -287 -288 289 -290 -291
v -292 -293 -294 -295 -296 -297 -298 -299 -300 301 -302 -303 -304 -305 -306
v -307 -308 -309 -310 -311 -312 -313 314 -315 -316 -317 -318 -319 -320 -321
v 322 -323 -324 -325 -326 -327 -328 329 -330 -331 -332 -333 -334 -335 -336
v -337 -338 339 -340 -341 -342 -343 -344 -345 -346 -347 -348 -349 350 -351
v -352 353 -354 -355 -356 -357 -358 -359 -360 -361 -362 -363 364 -365 -366
v -367 -368 -369 -370 -371 -372 -373 -374 -375 376 -377 -378 -379 -380 381
v -382 -383 -384 -385 -386 -387 -388 -389 -390 -391 -392 -393 -394 -395 396
v 397 -398 -399 -400 -401 -402 -403 -404 -405 -406 -407 -408 -409 -410 -411
v 412 -413 -414 -415 -416 -417 418 -419 -420 -421 -422 -423 424 -425 -426
v -427 -428 -429 -430 -431 -432 -433 -434 435 -436 -437 -438 -439 -440 -441
v -442 -443 -444 -445 -446 -447 -448 -449 450 -451 -452 -453 -454 -455 -456
v -457 458 -459 -460 -461 -462 -463 -464 465 -466 -467 -468 -469 470 -471
v -472 -473 -474 -475 -476 -477 -478 -479 -480 -481 482 -483 -484 -485 -486
v -487 -488 489 -490 -491 -492 -493 -494 -495 496 -497 -498 -499 -500 -501
v -502 -503 -504 -505 -506 -507 -508 -509 -510 -511 -512 513 -514 -515 -516
v 517 -518 -519 -520 -521 -522 -523 -524 -525 -526 -527 -528 529 -530 -531
v -532 -533 -534 -535 536 -537 -538 -539 -540 -541 542 -543 -544 -545 -546
v -547 -548 -549 -550 -551 -552 -553 -554 555 -556 -557 -558 -559 -560 -561
v -562 -563 -564 -565 566 -567 -568 -569 -570 -571 -572 -573 -574 575 -576
v -577 -578 -579 -580 581 -582 -583 -584 -585 -586 -587 -588 -589 -590 591
v -592 -593 -594 595 -596 -597 -598 -599 -600 -601 -602 -603 -604 605 -606
v -607 -608 -609 -610 -611 -612 -613 -614 -615 -616 -617 -618 -619 -620 621
v -622 -623 -624 -625 -626 -627 628 -629 -630 -631 -632 -633 634 -635 -636
v -637 -638 -639 -640 -641 642 -643 -644 -645 -646 -647 -648 -649 650 -651
v -652 -653 -654 -655 -656 -657 -658 -659 -660 -661 -662 -663 664 -665 -666
v -667 -668 -669 670 -671 -672 -673 -674 -675 -676 -677 -678 -679 -680 -681
v -682 683 -684 -685 -686 687 -688 -689 -690 -691 -692 -693 -694 -695 -696
v -697 -698 699 -700 -701 -702 703 -704 -705 -706 -707 -708 -709 -710 -711
v -712 -713 -714 -715 716 -717 -718 -719 -720 -721 -722 -723 -724 -725 -726
v -727 -728 729 0
s SATISFIABLE
c 
c Models         : 1
c Calls          : 1
c Time           : 0.907s (Solving: 0.90s 1st Model: 0.81s Unsat: 0.09s)
c CPU Time       : 0.900s

Decoding it, we see that the first cell must have value 6, the second the value 9 and so on.

SAT Solver APIs

In addition to the DIMACS CNF file format, many SAT solvers also allow one to describe SAT problems via an API. For instance,

The MiniSat SAT solver has a rather clean C++ implementation and API and it is thus widely used in many applications and when developing new solver features

namespace Minisat {
class Solver {
public:
  Var newVar(bool polarity = true, bool dvar = true); // Add a new variable
  bool addClause(const vec<Lit>& ps); // Add a clause
  bool solve();  // Search without assumptions.
  ...

The Sat4j used in Round 10 of CS-A1140 Data Structures and Algorithms is implemented in Java and has a Java API.
The Z3 solver, that we use later in this course, allows also non-Boolean variables, linear equations etc and has bindings to .net, C, C++, Python, Java and OCaml.

PySAT

PySAT is a Python wrapper providing a unified API to many SAT solvers. It is easy to install with pip. For instance, in the Aalto linux machines one can say the following in a console to create a Python virtual environment and install PySAT in it:

virtualenv pysat-venv
source pysat-venv/bin/activate
pip install python-sat

The unified API of PySAT allows one to create the CNF instance, solve it, and decode the result in one Python program. For instance, a full program for creating and solving Sudoku problems with a SAT solver is given below. The program may seem rather long but it includes model validation and lots of assertions. Its essential parts are the encode and solve_and_decode methods, which basically consists of for-loops and list comprehensions only.

#!/usr/bin/python3

"""Solving Sudoku instances by using the PySAT SAT solver package."""

import argparse
from typing import Tuple

from pysat.formula import CNF
from pysat.solvers import Solver

D = 3    # Subgrid dimension
N = D*D  # Grid dimension

# The symbols allowed in the Sudoku instance text file
DIGITS = {'1': 1, '2': 2, '3': 3, '4': 4, '5': 5,
          '6': 6, '7': 7, '8': 8, '9': 9}
NOCLUE = '.'


def read_clues(filename: str):
    """Read a Sudoku instance (a set of clues) from a file.
    Return a N*N matrix where each entry is either None or
    the clue at that cell."""
    clues = {}
    with open(filename, 'r', encoding='UTF-8') as handle:
        row = 0
        for line in handle.readlines():
            line = line.strip()
            assert len(line) == N, f'Malformed line "{line}"'
            for (column, entry) in enumerate(line):
                assert entry in DIGITS or entry == NOCLUE, f'Malformed line "{line}"'
                if entry != NOCLUE:
                    clues[(row+1, column+1)] = int(entry)
            row += 1
    assert row == N, f'Unexpected number of clue lines ({row}, expected {N})'
    return clues


def encode(clues) -> CNF:
    """Encode the given clues in a PySAT CNF SAT instance."""

    def var(row: int, column: int, value: int) -> int:
        """A helper: get the CNF variable number (a positive integer) for
        the variable v_{row,column,value} encoding the fact that
         the cell at (row,column) has the value "value"."""
        assert 1 <= row <= N and 1 <= column <= N and 1 <= value <= N
        return (row-1)*N*N+(column-1)*N+(value-1)+1

    # The formula in CNF, empty in the beginning
    cnf = CNF()

    # Build the clauses in a list
    for row in range(1, N+1):  # row runs over 1,...,N
        for column in range(1, N+1):
            # The cell at (row,column) has at least one value
            cnf.append([var(row, column, value) for value in range(1, N+1)])
            # The cell at (row,column) has at most one value
            for value in range(1, N+1):
                for walue in range(value+1, N+1):
                    cnf.append([-var(row, column, value),
                                -var(row, column, walue)])
    for value in range(1, N+1):
        # Each row has the value
        for row in range(1, N+1):
            cnf.append([var(row, column, value) for column in range(1, N+1)])
        # Each column has the value
        for column in range(1, N+1):
            cnf.append([var(row, column, value) for row in range(1, N+1)])
        # Each subgrid has the value
        for sr in range(0, D):
            for sc in range(0, D):
                cnf.append([var(sr*D+rd, sc*D+cd, value)
                            for rd in range(1, D+1)
                            for cd in range(1, D+1)])
    # The clues must be respected
    for (row, column) in clues:
        value = clues[(row, column)]
        cnf.append([var(row, column, value)])

    return cnf


def err(msg: str):
    """Called if solution construction or validation fails.
    Does not return."""
    raise Exception(msg)


def solve_and_decode(clues, cnf: CNF, all_solutions: bool) -> None:
    """Solve and decode the solutions of the given
    propositional CNF SAT instance
    encoding a Sudoku instance."""

    # The number of the encoding variables in the instance.
    nof_encoding_vars = N * N * N

    def var_inv(cnf_var: int) -> Tuple[int, int, int]:
        """The inverse of the encode.var method.
        Return the CNF variable for
        the encoding variable v_{row,column,value} denoting that
        the cell at (row,column) has the value "value"."""
        assert 1 <= cnf_var <= nof_encoding_vars
        row = ((cnf_var - 1) // (N * N)) + 1
        column = ((cnf_var - 1) // N % N) + 1
        value = ((cnf_var - 1) % N) + 1
        assert 1 <= row <= N and 1 <= column <= N and 1 <= value <= N
        assert (row-1)*N*N+(column-1)*N+(value-1)+1 == cnf_var
        return (row, column, value)

    # Create a solver and give the CNF encoding to it
    solver = Solver(bootstrap_with=cnf)

    # Enumerate and validate all solutions
    nof_solutions = 0
    for model in solver.enum_models():
        # "model" is now a truth assignment that satisfies the CNF formula
        # decode it into the corresponding Sudoku solution
        solution = {}
        for literal in model:
            if 0 < literal <= nof_encoding_vars:
                # The positive encoding literals give us the values
                (row, column, value) = var_inv(literal)
                if (row, column) in solution:
                    err(f'Found a solution with two values '
                        f'for the cell at ({row}, {column})')
                solution[(row, column)] = value
        validate_solution(solution, clues)
        nof_solutions += 1
        print(f'Solution: {nof_solutions}')
        for row in range(1, N+1):
            print(' '+' '.join([str(solution[(row, column)])
                                for column in range(1, N+1)]))
        print('')
        if not all_solutions:
            break
    print(f'Found {nof_solutions} solutions')


def validate_solution(solution, clues) -> None:
    """Validate that the "solution" fulfills
    all the Sudoku solution requirements.
    Only for testing the encoding process correctness.
    raises an Exception if the validation fails.
    """
    # Each cell should have a number in it
    for row in range(1, N+1):
        for column in range(1, N+1):
            if (row, column) not in solution:
                err(f'A solution with no value '
                    f'for the cell at ({row},{column})')
    all_values = set(range(1, N+1))
    # Each row should contain all the numbers
    for row in range(1, N+1):
        values = {solution[(row, column)] for column in range(1, N+1)}
        if values != all_values:
            err(f'A solution where the row {row} '
                f'does not contain all the values')
    # Each column should contain all the numbers
    for column in range(1, N+1):
        values = {solution[(row, column)] for row in range(1, N+1)}
        if values != all_values:
            err(f'A solution where the column {column} '
                f'does not contain all the values')
    # Each sub-grid should contain all the numbers
    for sr in range(0, D):
        for sc in range(0, D):
            values = {solution[(sr*D+rd, sc*D+cd)]
                      for rd in range(1, D+1)
                      for cd in range(1, D+1)}
        if values != all_values:
            err(f'A solution where a sub-grid '
                f'does not contain all the values')
    # The clues must be respected
    for (row, column) in clues:
        clue = clues[(row, column)]
        if solution[(row, column)] != clue:
            err(f'A solution where the clue at the cell '
                f'({row+1},{column+1}) is not respected')


def main():
    """The main method for command line use."""
    argp = argparse.ArgumentParser(
        description='Solve Sudoku problems with a SAT solver.',
        formatter_class=argparse.ArgumentDefaultsHelpFormatter)
    argp.add_argument('clues', type=str,
                      help='the Sudoku instance (a set of clues)')
    argp.add_argument('--all_solutions', action='store_true',
                      help='enumerate all solutions')
    args = argp.parse_args()

    # Read the clues from the file given as the first argument
    clues = read_clues(args.clues)

    # Encode them as a CNF SAT instance
    cnf = encode(clues)

    # Solve the formula and decode the found solutions
    solve_and_decode(clues, cnf, args.all_solutions)


if __name__ == '__main__':
    main()

When the above program is executed with python3 sudoku_pysat.py sudoku-royle.txt --all the result output is

Solution: 1
9 3 7 8 4 5 1 2
8 7 5 1 2 9 3 6
2 5 9 6 3 8 7 4
3 2 6 5 1 4 8 7
6 8 2 4 7 3 9 1
4 1 3 9 8 6 2 5
1 9 4 7 5 2 6 8
5 6 1 2 9 7 4 3
7 4 8 3 6 1 5 9

Found 1 solutions