Tutorial simulations¶
This page lists some tutorial simulations that can be used as the basis for simulations or to inspire your own ideas. It is not necessary to go through all the tutorials, but they demonstrate some technicalities and typical errors involved in running simulations.
The tutorials are:
- Getting started
- Different atoms
- About temperature
- Potential problems
- Take control
- Absolute precision
To run these simulations, you need to have all the simulation tools and necessary libraries installed. Follow the instructions on Setting up the simulation environment if you have not installed them yet.
Visualization¶
For basic plotting of data, you can use for example Gnuplot, matplotlib, Matlab or Grace.
Use of matplotlib is encouraged as it is an extremely versatile plotting tool and it uses a similar syntax as Matlab.
matplotlib is a Python module which means that you can import it to your Python script and call the plotting methods from there.
The friction_tools module has also a couple of plotting functions which actually use the matplotlib.
For visualization of atomic structures, VMD is probably the easiest and most powerful to use and we have provided access and an introduction here: VMD. A couple of alternatives to VMD are xcrysden, jmol, ash and the GUI of ASE.
Getting started¶
This tutorial shows how to
- run a simulation
- create atoms
- create interactions
- assign velocities
- run a simulation
- visualize the simulation
and introduces the methods
friction_tools.FrictionSimulation.create_atoms()friction_tools.FrictionSimulation.create_interaction()friction_tools.FrictionSimulation.set_velocities()friction_tools.FrictionSimulation.create_dynamics()friction_tools.FrictionSimulation.save_trajectory_during_simulation()friction_tools.FrictionSimulation.run_simulation()friction_tools.trajectory_to_xyz()
Create a text file containing the code below using your favorite text editor.
For instance, launch Emacs by typing emacs getting_started.py on the command line, copy and paste
the text below, and save with ctrl-X ctrl-S and quit with ctrl-X ctrl-C
(or use gedit by typing gedit getting_started.py if you find Emacs intimidating):
#! /usr/bin/env python
import friction_tools as ft
# create the simulation containing two atoms
simu = ft.FrictionSimulation()
simu.create_atoms(element='C',positions=[[0, 0, 0],
[6, 0, 0]])
# create an interaction between the two atoms
#simu.create_interaction(['C','C'],strength=10.0,equilibrium_distance=5.0)
# give the atoms some initial velocities
vs = [[0.1, 0, 0],[-0.1, 0, 0]]
#simu.set_velocities(indices=range(2), velocity=vs)
# tell that we want to run the simulation with default settings
simu.create_dynamics()
# tell that we want to record the movement of the atoms
simu.save_trajectory_during_simulation(interval=5)
# run the simulation for 1000 fs
print "starting simulation"
simu.run_simulation(time=1000.0)
print "finished simulation"
# after finishing, create an xyz-file for viewing what happened
ft.trajectory_to_xyz()
Once you’ve created the file, execute it from the command line with
python getting_started.py. Make sure that all the necessary components are
accessible to Python. First of all, make sure you are in the same directory where
you created the input file. If you have some import errors, make sure that you are also
in the directory where you set up the simulation environment or you have added that directory to
the $PYTHONPATH environment variable. If you have problems, ask for help so that technicalities
get sorted out.
The simulation should be very fast (most of the time is actually spent loading the libraries)
and if all goes well, you should find the file simulation.xyz in the directory.
(You can change the name of the output file by adding the argument filename_out to
trajectory_to_xyz().)
The file contains the positions of the atoms in your simulation as a function of time.
You can look at what happened with a visualization tool for atomistic structure. If
VMD is installed, which is true for the Linux workstations at the university, you can launch
it using command vmd simulation.xyz. See VMD page, for further instructions on using VMD.
Another alternative, especially if VMD is not installed, is to use the simple Java visualizer
called ash, which is included with the tools package. You can launch it by typing java -jar $HOME/path/to/tools/ash.jar
on the command line (if you make an alias for this command, like
alias look="java -jar ~/path/to/tools/ash.jar", you can launch it simply by typing look). Then type
open xyz simulation.xyz to open the written geometry file. You can scroll
the animation by clicking on the visualization window and then holding the n (next) or
p (previous) keys. To see the commands the program understands, type list command.
You may notice the result wasn’t very exciting. To make the atoms move, uncomment
the line #simu.set_velocities(indices=range(2), velocity=vs)
(remove the hash # in front - the program ignores everything coming after a hash)
and rerun the simulation. This command tells that the starting velocity of atom 0
(indexing starts from 0) is [0.1, 0, 0] and the velocity of atom 1 is [-0.1, 0, 0].
What happens now?
To make the atoms interact, uncomment
the line #simu.create_interaction(['C','C'],strength=10.0,equilibrium_distance=5.0).
How does this change things?
You may also change the initial velocities or play around otherwise to get an
idea of what the commands do.
Try for instance vs = [[0, 0, 0.5],[0, 0, -0.5]].
Different atoms¶
This tutorial shows how to
- create atoms of different chemical species
- specify atoms by their simulation indices
- check the system you’ve created during setup
- constrain the dynamics of a set of atoms
- extract data on groups of atoms
and introduces the methods
friction_tools.FrictionSimulation.create_slab()friction_tools.FrictionSimulation.list_atoms()friction_tools.FrictionSimulation.get_indices_by_element()friction_tools.FrictionSimulation.get_indices_z_less_than()friction_tools.FrictionSimulation.print_stats_during_simulation()friction_tools.FrictionSimulation.gather_energy_and_temperature_during_simulation()friction_tools.FrictionSimulation.gather_average_position_during_simulation()friction_tools.FrictionSimulation.fix_positions()friction_tools.FrictionSimulation.duplicate_atoms()friction_tools.FrictionSimulation.attach_with_springs()
To construct meaningful simulations, you usually need different kinds of atoms in your system. Some may be of different chemical species. Some may represent the surface of a material, while others are in the bulk. You may also want to mimic a situation where you are simulating only a small part of a larger system and want to impose boundary conditions on your setup. To do all this, you need to be able to distinguish the atoms in your system.
Create a file, say, different_atoms.py with the contents:
#! /usr/bin/env python
import friction_tools as ft
simu = ft.FrictionSimulation()
# create a thin glod slab - this will make the system
# periodic in x- and y-directions
simu.create_slab(element='Au',xy_cells=3,z_cells=2,top_z=0.0)
# create a single silver atom
simu.create_atoms(element='Ag',positions=[[5, 5, 10]])
# check the system
simu.list_atoms()
# stop here - remove 'quit()' to carry out the rest of the script
quit()
# create interactions
simu.create_interaction(['Au','Au'], strength=1.0, equilibrium_distance=2.39)
#simu.create_interaction(['Au','Ag'], strength=0.1, equilibrium_distance=4.0)
# list the indices of gold and silver atoms
au_indices = simu.get_indices_by_element('Au')
ag_indices = simu.get_indices_by_element('Ag')
# also list the atoms who are at the bottom of the gold slab
bottom_indices = simu.get_indices_z_less_than(-3.5)
# make the silver atom start with a high velocity towards the gold slab
simu.set_velocities(indices=ag_indices, velocity=[0, 0, -0.5])
# constrain the gold slab?
constraint = 0
if constraint == 1:
# prevent the gold slab from moving
simu.fix_positions(au_indices)
elif constraint == 2:
# prevent the bottom of the gold slab from moving
simu.fix_positions(bottom_indices)
elif constraint == 3:
# create 'ghost' atoms at the bottom of the slab and attach the bottom to them
simu.duplicate_atoms(element='C',indices=bottom_indices)
c_indices = simu.get_indices_by_element('C')
simu.attach_with_springs(c_indices, bottom_indices, strength=1.0, cutoff=3.0)
simu.fix_positions(c_indices)
# tell that we want to run the simulation with default settings
simu.create_dynamics(dt=1.0)
# tell that we want to collect information:
# - all positions
simu.save_trajectory_during_simulation(interval=10.0)
# - monitor the simulation by printing info to stdout
simu.print_stats_during_simulation(interval=50.0)
# - record energies in a file (default name 'energy.txt')
simu.gather_energy_and_temperature_during_simulation(interval=10.0)
# - record the x y z coordinates of the centre of mass of the Au slab
simu.gather_average_position_during_simulation(interval=10.0,indices=au_indices,filename='au_position.txt')
# - record the x y z coordinates of the Ag atom
simu.gather_average_position_during_simulation(interval=10.0,indices=ag_indices,filename='ag_position.txt')
# time the simulation
import time
t0 = time.time()
print "starting simulation"
simu.run_simulation(time=2000.0)
print "finished simulation"
t1 = time.time()
print "time taken {ti} s".format(ti=str(int(t1-t0)))
ft.trajectory_to_xyz()
If you run this as it is, the simulation will terminate at quit(). Before that,
the system will have been created and an atom-by-atom description including indices
and coordinates shown. You may look at the information that is available and try to
deduce what the system is like based on it.
To access the actual simulation, remove quit() and run again. If you take a look at
what happens, you’ll see that the simulation is of a silver atom hitting
a gold sheet at a high velocity. However, there was no interaction between the gold and the silver,
so no collision either. Uncomment
#simu.create_interaction(['Au','Ag'], strength=0.1, equilibrium_distance=4.0)
to enable the interaction and rerun. What happens now?
You can also try, for instance, changing the initial velocity of the silver atom
and see how this affects the behaviour.
You may notice that the simulation produced output due to the simu.gather_*
methods. You may want to have a look at what the files contain. For instance,
gather_average_position_during_simulation()
records the centre of mass
position of the atoms it monitors, and one of these methods produced
the file au_position.txt containing the collective movement of the gold slab.
If you plot the z-coordinate, you should see that the slab started to move due to the impact.
You can use the script:
import friction_tools as ft
posi = ft.read_array_from_file('au_position.txt')
ft.plot_array(posi[:,2])
ft.hold_plots()
to do the plotting. The script first reads in the data from the file in the array posi
and then plots the third column, posi[:,2]
(indexing starts from 0, so [:,2] refers to the third column). Similar plotting commands
can be included in any script, of course, to get your plots automatically once the
run has finished.
You can also create a plot quickly with for instance Gnuplot.
Give the command gnuplot on the command line to launch the plotter.
Then, to plot the z-coordinate of
the gold slab, which should be the third column of the file au_position.txt,
give the command plot 'au_position.txt' using 3 (or more simply p 'au_position.txt' u 3).
What can you do if, instead of a gold slab, you’d like to simulate the surface of
a thick piece of gold? Simulating a larger system is possible, but this
simulator is not efficient enough to handle more than some tens of thousands of atoms.
Even state-of-the-art simulators can manage ‘only’ some billions of atoms given enough computing power.
Instead of building a huge simulation, the trick is to make the slab behave as if it was attached to
more atoms. You can try a few ways of how to do this by editing the value of
constraint between 1 and 3. These options will allow you to
freeze the whole or a part of the gold slab, or even anchor it using springs.
Take a look at the simulation using these different options. You may
also look at the output data. Do you see differences? Which constraint seems
like the most reasonable approximation for mimicking the surface of a bulk sample?
Are there differences in how quickly the computation is carried out?
One more thing to notice here: The method simu.create_slab() automatically
makes the system periodic in x and y directions using
periodic boundary conditions.
Essentially, this means that particles near the edge of the simulation box (which is
also automatically set to have the area of 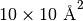 in the xy-plane)
interact with particles on the other edge. So, the gold atoms actually form
an infinite surface, not just the small piece explicitly simulated.
To demonstrate how the periodicity works, try changing the the initial position of
the silver atom to
in the xy-plane)
interact with particles on the other edge. So, the gold atoms actually form
an infinite surface, not just the small piece explicitly simulated.
To demonstrate how the periodicity works, try changing the the initial position of
the silver atom to [5, 15, 10]. If you do that, it will be outside the simulation
box, but due to the periodic boundaries, it behaves as if it was inside (or, if a
copy of the gold slab existed outside of the box).
You can also see what happens if you turn off the periodicity by adding the command
simu.system.set_pbc([False, False, False]) after creating the slab. The
effect is more pronounced if you also remove constraints or give the silver
atom a higher initial velocity.
About temperature¶
This tutorial shows how to
- set up different kinds of dynamics
- control the temperature
- anticipate artifacts due to thermostatting
Let’s continue with the same example as in the previous tutorial. If you skipped it or deleted your input files already, you may start with the script:
#! /usr/bin/env python
import friction_tools as ft
simu = ft.FrictionSimulation()
simu.create_slab(element='Au',xy_cells=3,z_cells=2,top_z=0.0)
simu.create_atoms(element='Ag',positions=[[5, 5, 10]])
simu.create_interaction(['Au','Au'], strength=1.0, equilibrium_distance=2.39)
simu.create_interaction(['Au','Ag'], strength=0.1, equilibrium_distance=4.0)
au_indices = simu.get_indices_by_element('Au')
ag_indices = simu.get_indices_by_element('Ag')
bottom_indices = simu.get_indices_z_less_than(-3.5)
simu.set_velocities(indices=ag_indices, velocity=[0, 0, -0.5])
constraint = 0
if constraint == 1:
simu.fix_positions(au_indices)
elif constraint == 2:
simu.fix_positions(bottom_indices)
elif constraint == 3:
simu.duplicate_atoms(element='C',indices=bottom_indices)
c_indices = simu.get_indices_by_element('C')
simu.attach_with_springs(c_indices, bottom_indices, strength=1.0, cutoff=3.0)
simu.fix_positions(c_indices)
# the thermostat will be added here:
simu.create_dynamics(dt=1.0)
simu.save_trajectory_during_simulation(interval=10.0)
simu.print_stats_during_simulation(interval=50.0)
simu.gather_energy_and_temperature_during_simulation(interval=10.0)
simu.gather_average_position_during_simulation(interval=10.0,indices=au_indices,filename='au_position.txt')
simu.gather_average_position_during_simulation(interval=10.0,indices=ag_indices,filename='ag_position.txt')
import time
t0 = time.time()
print "starting simulation"
simu.run_simulation(time=5000.0) # increased the simulation time
print "finished simulation"
t1 = time.time()
print "time taken {ti} s".format(ti=str(int(t1-t0)))
ft.trajectory_to_xyz()
If you look
at the output from the previous simulations or run the above code,
you should see that the temperature (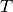 )
of your system varies but the total energy
)
of your system varies but the total energy 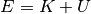 is conserved
(
is conserved
(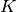 and
and  are the kinetic and potential energies). This is a
fundamental property of Newtonian mechanics
and the Verlet algorithm
used for integrating the equations of motion.
are the kinetic and potential energies). This is a
fundamental property of Newtonian mechanics
and the Verlet algorithm
used for integrating the equations of motion.
Actually, the temperature is just proportional to the average kinetic energy
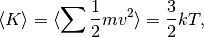
where 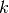 is the Boltzmann constant,
and conservation of energy means that any changes in potential energy
is the Boltzmann constant,
and conservation of energy means that any changes in potential energy
 are reflected in changes in
are reflected in changes in 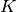 and so also the temperature.
Often, however, it makes more sense to keep the temperature
constant instead of total energy. For instance, if your purpose is to simulate
a part of a larger system, heat should be allowed to flow between the simulated system
and the imagined surroundings.
In statistical mechanics,
this is called the
canonical ensemble or the NVT ensemble
(number of particles
and so also the temperature.
Often, however, it makes more sense to keep the temperature
constant instead of total energy. For instance, if your purpose is to simulate
a part of a larger system, heat should be allowed to flow between the simulated system
and the imagined surroundings.
In statistical mechanics,
this is called the
canonical ensemble or the NVT ensemble
(number of particles 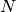 , volume
, volume 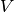 , and temperature
, and temperature 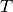 are constant).
are constant).
A thermostat is an algorithm or a modification of the equations of motion which allows the system to exchange kinetic energy with imaginary surroundings. There are many ways to implement a thermostat, and in this toolset the Langevin thermostat is used.
To turn on the thermostat, just add the temperature argument in the dynamics
definition, e.g., simu.create_dynamics(dt=1.0, temperature=300).
Also remove all constraints from the system (constraint = 0) and maybe
increase the length of the simulation too.
Then run the simulation.
How do the energy components and total energy  change over time now? (Plot!)
What about the temperature?
What do you see if you look at the actual simulation?
change over time now? (Plot!)
What about the temperature?
What do you see if you look at the actual simulation?
(Note that there is also a command
set_temperature().
However, this command only gives the atoms initial velocities according to the
Maxwell-Boltzmann distribution.
It does not turn on the thermostat.)
You should have noticed that the energy and temperaure fluctuate, i.e., change randomly around some average. In this case, the average is defined by the temperature of 300 K. However, if you look at the simulation, you’ll see that the silver atom that was initially moving at a high velocity halts due to no apparent reason. This is an artifact caused by the thermostat - the high velocity of the silver atom corresponds to a high temperature, and so the thermostat applies a decelarating force on it. If you plot the movement of the gold sheet, you’ll also notice it jiggles around a bit - another example of weird behaviour due to the thermostat.
You can add the argument strength to the dynamics creating
method, e.g., simu.create_dynamics(dt=1.0, temperature=300, strength=0.1) to control
how rapidly the target temperature is reached. The default is strength=0.01.
If you increase the strength, the temperature approaches the target value faster,
but the true dynamics are lost (just look at how the silver atom behaves).
On the other hand, if you decrease the strength, dynamics are replicated better,
but it takes longer to reach the equilibrium temperature. In essence, this
represents the rate of heat conduction between the simulated system and its surroundings.
If your purpose is to simulate the system at a certain temperature,
you have to wait until the temperature has reached an equilibrium (thermalization)
before starting actual data collection. One trick to speed things up is to
first simulate a while with a strong thermostat and then tone down the strength
for the proper simulation.
To prevent the gold from collectively moving around, you can reintroduce
a constraint, say, constraint = 2. To make the thermostat ignore the
silver atom and only control the temperature of the slab, try
simu.create_dynamics(dt=1.0, temperature=300, coupled_indices=au_indices).
Then rerun the simulation. You may notice that the temperature is not 300 K anymore.
This is fine, since the provided monitoring tools automatically calculate the
temperature based on all the particles in the system. If some are not allowed to move,
their temperature is 0 K and they pull the average temperature down.
The fast-moving silver atom on the other hand has a lot of kinetic energy
and it makes the temperature of the whole system high. The temperature of the
unconstrained part of the gold slab should be at 300 K.
Potential problems¶
This tutorial shows how to:
- examine interactions
- compare interactions, structure, and temperature
How atoms interact to form bonds, molecules, solids etc. is an extremely deep topic and fundamental to much of materials science. Describing these interactions is almost never simple since atoms interact via their electrons, whose behaviour is governed by (relativistic) quantum mechanics. To simulate all the phenomena that emerge from the electronic structure of matter is computationally very challenging and we cannot do it here. Instead, we use a very simple pair interaction model (a truncated Lennard-Jones potential), where the energy of each interacting atom pair only depends on their distance. This is enough for seeing some interesting qualitative results, but do not think that the interactions we use are a complete representation of how atoms truly behave.
To see what the energy of an atom pair in our simulation looks like, you can run the script:
#! /usr/bin/env python
import friction_tools as ft
simu = ft.FrictionSimulation()
simu.create_atoms('Au', [[0,0,0], [0,0,1.7]])
simu.create_interaction(['Au','Au'], 1.0, 2.0)
simu.create_dynamics(dt=1.0)
simu.fix_positions([0])
simu.fix_velocities([1], [0,0,0.01])
simu.print_stats_during_simulation(interval=1.0)
simu.gather_energy_and_temperature_during_simulation(interval=1.0,filename='energy.txt')
simu.gather_average_position_during_simulation(interval=1.0,indices=[1],filename='separation.txt')
simu.gather_average_force_during_simulation(interval=1.0,indices=[1],filename='force.txt')
simu.run_simulation(time=150)
This will create a system with two atoms. One is kept stationary while the other moves
with constant velocity. Thus the recorded energy,  , (first column of
, (first column of energy.txt)
is actually the energy of the pair interaction as a function of distance.
Similarly, the force,  , is recorded in
, is recorded in force.txt.
What does the potential energy look like?
The interaction is defined by only two parameters, strength and equilibrium_distance.
These are the depth of the potential energy well (in eV) and the atomic separation (in Å)
where the energy minimum occurs. These define the energy and length scales of
your simulation. For instance, if you make the interactions strong, you will need
higher temperatures to break the atomic bonds. Similarly, changing the length
scale changes the size of a stable system.
This is demonstrated in the following:
#! /usr/bin/env python
import friction_tools as ft
simu = ft.FrictionSimulation()
simu.create_slab(element='Au',xy_cells=3,z_cells=2,top_z=0.0)
simu.create_interaction(['Au','Au'], strength=1.0, equilibrium_distance=2.375)
simu.create_dynamics()
simu.print_stats_during_simulation(interval=50.0)
simu.save_trajectory_during_simulation(interval=50.0)
simu.run_simulation(time=10000.0)
ft.trajectory_to_xyz()
If you run this simulation as it is, not much happens since the created slab
is an equilibrium configuration of the given interaction. However, try
changing the equilibrium distance of the interaction from 2.375 to, say, 2.2 and
rerun. You may also try 2.6. What happens? Do you understand why the
system behaves as it does?
If you change the slab creating command to, e.g.,
simu.create_slab(element='Au',xy_cells=4,z_cells=2,top_z=0.0), the slab
will fit 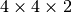 unit cells in the simulation volume.
(The size of the simulation box is kept the same, but more atoms are
inserted.) Can you determine the equilibrium distance for which
this is a stable configuration? Note that
unit cells in the simulation volume.
(The size of the simulation box is kept the same, but more atoms are
inserted.) Can you determine the equilibrium distance for which
this is a stable configuration? Note that create_slab method creates a
FCC lattice structure
and prints the lattice constant for your convenience.
Returning back to the equilibrium configuration, you may instead vary interaction
strength. Turn on the thermostat and set the temperature at, for instance, 300 K
with simu.create_dynamics(temperature = 300). What happens? How does the behaviour change
if you decrease the interaction strength?
Take control¶
This tutorial shows how to:
- continue a previous simulation
- build the system dynamically
- monitor and control simulations on the go
and introduces the methods
friction_tools.FrictionSimulation.fix_velocities()friction_tools.FrictionSimulation.remove_constraints()friction_tools.FrictionSimulation.continue_from_trajectory()
It’s often convenient to run a simulation in parts, check the results, and continue from where you left. Or, if the simulation fails at some point, it is convenient to reload from the middle of the simulation. This can be done by creating a trajectory file during one simulation and reloading the system from this trajectory to start a second.
To show how this works, this simulation is split in two parts. The first is:
#! /usr/bin/env python
import friction_tools as ft
simu = ft.FrictionSimulation()
# create two slabs
simu.create_slab(element='Au',xy_cells=3,z_cells=2,top_z=0.0)
simu.create_slab(element='Ag',xy_cells=4,z_cells=2,bottom_z=5.0)
# create interactions
simu.create_interaction(['Au','Au'], 1.0, 2.375)
simu.create_interaction(['Ag','Ag'], 1.0, 1.781)
simu.create_interaction(['Au','Ag'], 0.1, 2.0)
au_indices = simu.get_indices_by_element('Au')
ag_indices = simu.get_indices_by_element('Ag')
bottom_indices = simu.get_indices_z_less_than(-3.5)
top_indices = simu.get_indices_z_more_than(8.0)
simu.create_dynamics(dt=1.0, temperature=300)
simu.save_trajectory_during_simulation(interval=50.0)
simu.print_stats_during_simulation(interval=50.0)
# time the simulation
import time
t0 = time.time()
# fix the bottom slab and make the top slab move down
simu.fix_velocities(top_indices, [0, 0, -0.005], [True,True,True])
simu.set_temperature(300)
simu.fix_positions(bottom_indices)
print "starting simulation, pushing down"
simu.run_simulation(time=500.0)
# make both slabs stationary
simu.remove_constraints()
simu.fix_positions(top_indices)
simu.fix_positions(bottom_indices)
print "continue simulation, hold still"
simu.run_simulation(time=500.0)
# make the top slab move up
simu.remove_constraints()
simu.fix_velocities(top_indices, [0, 0, 0.002], [True,True,True])
simu.fix_positions(bottom_indices)
print "continue simulation, pull up"
simu.run_simulation(time=3000.0)
ft.trajectory_to_xyz()
This simulates two slabs which are pressed together and then pulled apart.
Run the simulation. Then increase the strength of the Ag-Au interaction
to, for instance, simu.create_interaction(['Au','Ag'], 2.5, 2.0).
What happens to the surfaces of the slabs and why?
This simulation produced the trajectory file simulation.traj, which is
used as the starting point for the second simulation:
#! /usr/bin/env python
import friction_tools as ft
simu = ft.FrictionSimulation()
# load the end configuration of the previous simulation
simu.continue_from_trajectory()
# change all the atoms in the top slab to silver:
# - find the original top slab
high_indices = simu.get_indices_z_more_than(1)
# - copy the original top slab
simu.duplicate_atoms(element='Ag', indices=high_indices)
# - remove the original top slab
simu.remove_atoms(high_indices)
# replace the damaged bottom slab with a perfect one
# - find the original bottom slab
low_indices = simu.get_indices_z_less_than(1)
# - remove the original bottom slab
simu.remove_atoms(low_indices)
# - create a new slab
simu.create_slab(element='Au',xy_cells=3,z_cells=2,top_z=0.0)
# create interactions
simu.create_interaction(['Au','Au'], 1.0, 2.375)
simu.create_interaction(['Ag','Ag'], 1.0, 1.781)
simu.create_interaction(['Au','Ag'], 0.01, 2.5)
simu.set_temperature(300)
simu.create_dynamics(dt=1.0, temperature=300)
# fix the slabs
top_indices = simu.get_indices_z_more_than(11)
bottom_indices = simu.get_indices_z_less_than(-3.5)
simu.fix_positions(top_indices)
simu.fix_positions(bottom_indices)
simu.print_stats_during_simulation(interval=50.0)
# save the trajectory in a new file (so that we don't overwrite the old one)
simu.save_trajectory_during_simulation(interval=50.0, filename='test.traj')
# run for a while to let the system find a stable configuration
simu.run_simulation(time=2000.0)
# push the top slab down
simu.remove_constraints()
simu.fix_velocities(top_indices,[0,0,-0.002])
simu.fix_positions(bottom_indices)
threshold = 3.0
low_indices = simu.get_indices_z_less_than(threshold)
# approach the surface until the first silver atoms reach it
# this can be monitored, e.g., by counting the atoms below a certain
# threshold
while len(low_indices) == len(simu.get_indices_z_less_than(threshold)):
simu.run_simulation(100.0)
# write the geometry file - remember to read the correct trajectory
ft.trajectory_to_xyz(filename_in='test.traj')
This second part reads in the configuration obtained from the first simulation. The configuration is modified, though. First, the top slab that contained both silver and gold is changed to contain only silver. Also the damaged bottom slab is replaced by a perfect one. Although this is a fairly simple example, it demonstrates how complicated structures can be produced by stepwise dynamic simulations.
The last part of the simulation demonstrates how a simulation can be
controlled automatically by monitoring the system during the simulation.
It contains a loop which pushes the top slab down in short
steps. The loop is run until the top slab reaches a given threshold. Run the
simulation and look what happens. Can you set the threshold so that the simulation
terminates as the slabs come to contact?
Absolute precision¶
This tutorial shows how to:
- access the detailed information wrapped in the
FrictionSimulation.
and introduces the methods
Although the provided methods give you easy access to a set of
often needed routines, obviously they cannot answer every need you might
think of when building your simulation. Luckily, you can access
the simulation geometry and interactions directly to do essentially
whatever you want with the system. You do not have to go this far to create meaningful
simulations, but if you get frustrated by the limitations of the friction_tools
module, this is how you get around them.
Consider the script:
#! /usr/bin/env python
import friction_tools as ft
import math
import numpy as np
simu = ft.FrictionSimulation()
simu.create_slab(element='Ag',xy_cells=4,z_cells=4,bottom_z=0.0)
simu.create_interaction(['Ag','Ag'], 1.0, 1.781)
# define the center and radius of a sphere
lattice_constant = 10.0 / 4.0
center = np.array([1.5, 1.5, 1.5])*lattice_constant
radius = 2*lattice_constant
# take a picture of the system
simu.take_snapshot(filename='initial.png')
simu.write_xyzfile(filename='initial.xyz')
# check all the atoms and remove those that are not
# inside the sphere we just defined.
# note that the loop goes over the atoms backwards
# because we delete atoms as we go, which affects
# the end of the list of atoms but not the beginning
for atom in reversed(simu.system):
xyz = atom.position
separation = xyz - center
# calculate the distance between the atom and the
# center of the sphere
distance = math.sqrt(np.dot(separation, separation))
if distance > radius:
del simu.system[atom.index]
# take a picture of the system
simu.take_snapshot(filename='final.png')
simu.write_xyzfile(filename='final.xyz')
This simple script constructs a small ball of Ag atoms, which
you can see from the recorded snapshots.
There is no ready-made routine for this, but it’s an easy operation if you know the
coordinates of your atoms. And we do! The atoms are stored in
simu.system
(since the name of the FrictionSimulation was simu),
and the coordinate of atom  is in
is in
simu.system[i].position. All the operations you can do to
the atoms are explained in ASE documentation.
Similarly, if you need to tune the interactions in the system, you
can access the energy calculator as simu.calc.
It is a Pysic calculator object.