


Next: About this document ...
Note on Gibbs-Heaviside vector 'algebra'
P. Puska
Electromagnetics lab., Helsinki U. of Tech., Finland
Strictly speaking Gibbs-Heaviside (GH) vector algebra is not an algebra,
but rather a combination of cross product algebra
(an example of Lie algebra) and a scalar product.
However, GH 'algebra' is
contained in Clifford algebra
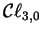 generated by
generated by
In
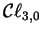 we can build a model of GH 'algebra' by making the identification
we can build a model of GH 'algebra' by making the identification
and using the identity relating the traditional cross-product and exterior
product (denoted by wedge) of
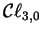 :
:
whenever
a,b are any real vectors in GH or
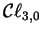 .
Thus the non-associativity of the cross-product can be understood
on the basis of the model of the cross-product we have just built in
.
Thus the non-associativity of the cross-product can be understood
on the basis of the model of the cross-product we have just built in
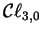 .
With the identity above it is straightforward to verify that
.
With the identity above it is straightforward to verify that
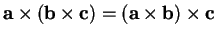 does not hold in general.
does not hold in general.
Perttu P Puska
2000-09-15
![]() generated by
generated by